【日报】浅谈随机分布及C++当中的实现
囧仙
2021-09-14 21:57:58
前言
为了缩短篇幅,本文**并不会**去探讨这些特定分布的来龙去脉,也并不会给出一些相关推导。这部分内容并不是文章的重点,读者可以通过百度等方式自行得到。我们关心的是 $\verb!random!$ 库里采取了什么样的算法。然而,由于作者能力有限(并且网上关于这方面的文章比较少),有些实现确实查阅不到资料。我只能尽量提供可能具有帮助的参考资料。
## 概念
### 分布
假如我们有个骰子,六个面上依次标为了 $1,2,\cdots 6$。现在抛一次骰子(每个面朝上的概率均等),设抛出来的点数为 $X$。容易发现,$X$ 的值是随机的,并且对于骰子上的六个值,$X$ 都有一定概率取得。像这样的只可能取有限个或至多可列个值的 $X$,称作**离散型随机变量**。对于刚刚的例子,很容易绘制出 $X$ 在不同取值时的概率:
$$
\def\arraystectch{1.5}
\begin{array}{c|c|c|c|c|c|c}
X & 1 & 2 & 3 & 4 & 5 & 6 \cr\hline
P & \frac{1}{6} & \frac{1}{6} & \frac{1}{6} & \frac{1}{6} & \frac{1}{6} & \frac{1}{6}
\end{array}
$$
当然了,$X$ 的可能取值可能有无数个。比如 $P(X=k)=\left(\frac{1}{2}\right)^k.k=1,2,\cdots$。这样的 $X$ 同样是离散型随机变量。
但是换个例子,比如说 $X$ 是在线段上取的任意一个点的数值,或者是在一个圆上取一个点到圆心的距离,你会发现貌似 $X$ 取到任意一个值的概率都是 $0$。但是我们可以描述 $X$ 取一个集合内的值的概率。比如在数轴上的线段 $[5,10]$ 内任取一个点,那么它在 $[6,8]$ 内的概率就是 $\frac{3}{5}$。对于这种的 $X$,我们称之为**非离散型随机变量**。
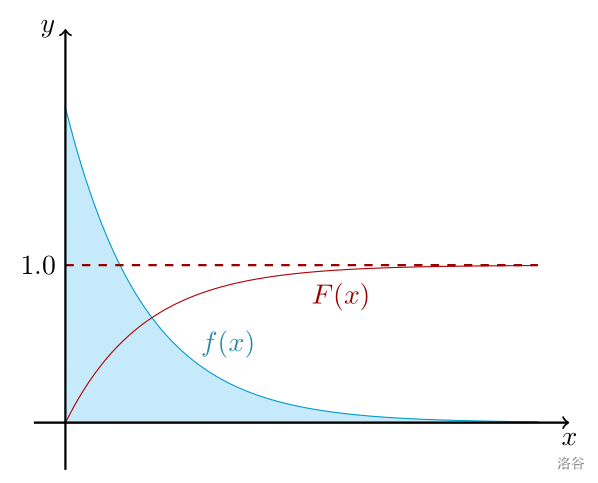
但是我们怎么描述多次观测一个非离散型随机变量得到的结果呢?这时候就要用到积分相关知识了。根据上文,我们可以描述一个非离散型随机变量在一定区间内的概率。首先定义**累积分布函数** $F(x)$,表示 $X$ 的取值在 $[0,x]$ 内的概率;接着可以定义出 $F(x)$ 在某点初的导数(假设 $F(x)$ 在此处可导。本文将会涉及到的所有累积分布函数都在定义域内可导),称作**概率密度函数** $f(x)=\frac{\mathrm dF(x)}{\mathrm dx}$。
容易发现,$f(x)$ 就是 $F(x)$ 的导数,$f(x)$ 积分后加上常数 $C$ 可得 $F(x)$。两者是可以互相转化的。下面是个例子:
### 均匀随机位生成器
接着简要提及一下标准库内的相关概念。
> **均匀随机位生成器**是返回无符号整数值的函数对象,可能结果范围中的每个值都(理想情况)拥有等概率。
从中我们可以得到,均匀随机位生成器应该是一个可以在指定范围内生成**均匀随机**的随机数的生成器。随机数分布内部需要有一个均匀随机数生成器,这将保证它生成出来的随机数确实是符合相关分布的。除此之外,标准里面还要求了一个均匀随机数生成器 $G$ 应当拥有以下几个表达式:
- $\verb!G::value_type!$:均匀随机数生成器返回值的类型。它应该是一个无符号整型。
- $\verb!G::min()!$:返回 $G$ 可以生成的随机数的最小值。最小值的类型应当为 $T$。
- $\verb!G::max()!$:返回 $G$ 可以生成的随机数的最大值。最大值的类型应当为 $T$。
- $\verb!G()!$:返回一个值域在 $[\verb!G::min()!,\verb!G::max()!]$ 里面的类型为 $T$ 的均匀的随机数。
在 $\verb!random!$ 库里已经内置了一些随机数引擎([线性同余](https://en.wikipedia.org/wiki/Linear_congruential_generator)算法、[梅森缠绕器](https://en.wikipedia.org/wiki/Mersenne_twister)算法、[延迟斐波那契](https://en.wikipedia.org/wiki/Lagged_Fibonacci_generator)算法),再配合上一些随机数引擎适配器实现好了一些现成的均匀随机位生成器(比如大名鼎鼎的 $\text{mt19937}$ 等等)。由于这部分内容不是我们的重点,因此不再赘述。有兴趣的读者可以参阅维基百科,以及 [$\textsf{cpp reference}$](https://zh.cppreference.com/w/cpp/numeric/random) 上面的相关叙述。
那么下面就是我们的主角。当前在 $\verb!random!$ 库里被提供的那些可生成服从特定分布的随机数的类。
**均匀分布**:
- $\verb!uniform_int_distribution !$:生成在固定范围上均匀的**整数**。
- $\verb!uniform_real_distribution!$:生成在固定范围上均匀的**实数**。
**伯努利分布**:
- $\verb!bernoulli_distribution!$:生成符合伯努利分布的 $\text{bool}$ 类型的值。
- $\verb!geometric_distribution!$:生成符合几何分布的整数值。
- $\verb!binomial_distribution !$:生成符合二项分布的整数值。
- $\verb!negative_binomial_distribution!$:生成一个符合负二项分布的整数值。
**泊松分布**:
- $\verb!poisson_distribution !$:生成符合泊松分布的**整数**值。
- $\verb!exponential_distribution!$:生成符合指数分布的**实数**值。
- $\verb!gamma_distribution !$:生成符合 $\Gamma$ 分布的实数值。
- $\verb!weibull_distribution !$:生成符合威布尔分布的实数值。
- $\verb!extreme_value_distribution!$:生成符合极值分布的实数值。
**正态分布**:
- $\verb!normal_distribution !$:生成符合标准正态(高斯)分布上的实数值。
- $\verb!lognormal_distribution!$:生成符合对数正态分布的实数值。
- $\verb!cauchy_distribution !$:生成符合柯西分布的实数值。
- $\verb!fisher_f_distribution !$:生成符合费舍尔分布的实数值。
- $\verb!student_t_distribution!$:生成符合学生分布上的实数值。
- $\verb!chi_squared_distribution!$:生成符合 $\chi^2$ 分布的实数值。
## 从均匀分布开始
考虑一个很简单的问题。你现在手头有一个均匀随机位生成器(不妨设为 $G$),可以随机生成 $16$ 位的无符号整数。现在你要用它实现一个函数 $\operatorname{rand}(a,b)$,使得它能够返回值在 $[a,b]$ 内的均匀的**随机整数**。应该怎么做?
很多人会用一个这样的方式来实现 $\operatorname{rand}(l,r)$:
```cpp
int rand(int a, int b){
return G() % (b - a + 1) + l;
}
```
嗯,这个 $\operatorname{rand}$ 函数看上去蛮对的。它把 $G$ 生成的随机数映射到了 $[0,b-a)$ 里面,然后把它加上 $a$,最终得到了值在 $[a,b]$ 内的随机数。但是只要仔细想一想,就会发现它里面存在的漏洞。首先是原理上的错误:$G$ 映射到 $[0,b-a)$ 是不均匀的。比如说,当 $a=0,b=60000$ 时,有两个数字映射到了 $2333$($2333$ 和 $62333$),但是仅有一个数字映射到了 $50000$。这样就会导致最终生成 $2333$ 的概率是生成 $50000$ 的两倍。其次还有实现上的漏洞:$b-a$ 有可能超过 $\text{int}$ 类型的最大值,发生不可预期的错误。
让我们看看 $\verb!random!$ 库是如何解决这些问题的。由于 $\verb!uniform_int_distribution!$ 库使用了模板,我们不妨设它的返回值为整型 $\text{Int}$。
- 与刚刚的做法类似,它把计算 $[a,b]$ 内的随机数的任务转换为了计算 $[0,b-a)$ 内的随机数的任务,再将结果加上 $a$。但它使用了一些 $\text{template}$ 的小技巧。通过获取 $\text{Int}$ 的**无符号形式** $\text{uInt}$,来防止发生溢出。这基于一个这样的补码的结论:
$$
\begin{aligned}\operatorname{unsigned}(u)&=
\begin{cases}
u & u\ge 0\cr
2^n+u & u<0\cr
\end{cases}\cr
\operatorname{unsigned}(u)-\operatorname{unsigned}(v)&=\begin{cases}
u-v & u\ge0,v\ge0 \cr
u-(2^n+v)& u\ge 0,v<0\cr
(2^n+u)-(2^n+v) &u<0,v<0 \cr
\end{cases}
\end{aligned}
$$
其中 $u$ 是一个 $n$ 位二进制有符号整数。负数 $u$ 的补码形式相当于先对它的所有二进制位取反,然后再加 $1$。取反操作本身就相当于让 $2^n-1$ 减去 $u$,再加上 $1$ 得到的就是 $2^n-u$。
然后就是对随机数生成器的最大最小值之差 $\mathrm{range}_{\mathrm{g}}=G_{\max}-G_{\min}$ 和现在需要生成的 $[a,b]$ 的最大最小值之差 $\mathrm{range}_{\mathrm{u}}=b-a$ 进行讨论。注意:$\mathrm{range}_{\mathrm{g}}$ 和 $\mathrm{range}_{\mathrm{u}}$ 比两者的值域少 $1$,这是为了防止程序中发生溢出。
- 第一种情况:$\mathrm{range}_{\mathrm{g}}>\mathrm{range}_{\mathrm{u}}$。这表明,我们需要缩小 $G$ 生成的随机数的值域,以至于达到 $u$ 的值域。设 $\mathrm{erange}_{\mathrm{u}}=\mathrm{range}_{\mathrm{u}}+1$,显然不会发生溢出。
不妨设 $\mathrm{range}_{\mathrm{g}}=r\cdot \mathrm{erange}_{\mathrm{u}}+s$。断言:只要不断让 $G$ 生成减去了 $G_{\min}$ 的随机数 $p$,直到 $p\in[0,r\cdot\mathrm{erange}_{\mathrm{u}})$,最终取 $p\div r$ 即可。显然,最终得到的 $p$ 肯定是在 $[0,r\cdot \mathrm{erange}_{\mathrm{u}})$ 里均匀的,通过除法映射到 $[0,\mathrm{erange}_{\mathrm{u}})$ 里也是均匀的,于是可以证明答案的正确性;由于 $s\le \min(\mathrm{erange}_{\mathrm{u}}-1,\mathrm{range}_{\mathrm{g}}-\mathrm{erange}_{\mathrm{u}})\le\left\lfloor\frac{1}{2}\mathrm{range}_{\mathrm{g}}\right\rfloor$,因此生成的 $p$ 在 $[r\cdot \mathrm{range}_{\mathrm{u}},\mathrm{range}_{\mathrm g}]$ 的概率不超过 $\frac{1}{2}$。因此期望只要进行两次生成,就能得到符合要求的随机数。时间复杂度为 $\mathcal O(1)$。
- 第二种情况:$\mathrm{range}_{\mathrm{g}}<\mathrm{range}_{\mathrm{u}}$。这表明,我们需要放大 $G$ 生成的随机数的值域,以至于达到 $u$ 的值域。设 $\mathrm{erange}_{\mathrm{g}}=\mathrm{range}_{\mathrm{g}}+1$,显然不会发生溢出。
不妨设 $\mathrm{range}_{\mathrm{u}}=r\cdot \mathrm{erange}_{\mathrm{g}}+s$。容易发现,$r>0$。现在我们**随机**生成一组 $(r'\in[0,r],s'\in[0,\mathrm{range}_{\mathrm{g}}]$(生成 $r'$ 可以通过递归处理),那么求出来的 $p=r'\cdot\mathrm{erange}_{\mathrm{g}}+s'$ 肯定是**均匀随机地**分布在 $[0,(r+1)\cdot \mathrm{erange}_{\mathrm{g}})$ 里面的。如何使得 $p$ 在 $[0,\mathrm{range}_{\mathrm{u}})$ 内呢?用一个最暴力的做法:若 ${p\ge\mathrm{range}_{\mathrm{u}}}$,那就**重新生成**,直到 $p\in[0,\mathrm{range}_{\mathrm{u}})$。答案的正确性比较显然,现在考虑时间复杂度的正确性。
不妨设 $r\in[2^{k-1},2^k)$。我们需要重新生成 $[0,r]$ 内的整数的次数期望为 $\frac{\mathrm{range}_{\mathrm{u}}-1}{\mathrm{range}_{\mathrm{u}}-1-\mathrm{range}_{\mathrm{g}}}$,也就是 $\frac{2^k}{2^k-1}$ 次。接着我们要做的就是把这些东西全部乘在一起:
$$
\left(\cdots \left(\left(\frac{2^1}{2^1-1}+1\right)\cdot \frac{2^2}{2^2-1}+1\right)\cdots\right)\cdot\frac{2^k}{2^k-1}+1
$$
这个式子最终会无限趋近 $k$ 加上一个常数,所以总复杂度为 $\mathcal O(\log_{\mathrm{range}_{\mathrm{g}}}\mathrm{range}_{\mathrm{u}})$。
- 第三种情况:$\mathrm{range}_{\mathrm{g}}=\mathrm{range}_{\mathrm{u}}$。这种情况就很简单了,直接返回 $G$ 生成的随机数即可,时间复杂度是 $\mathcal O(1)$。
这里给出一个模拟标准库写法的实现:
```cpp
#include<iostream>
#include<random>
typedef unsigned int u32;
typedef unsigned long long u64;
std::mt19937 MT;
u32 rand4(){ return MT() & 15; }
template <typename T>
T rand(T l, T r){
typedef typename std::make_unsigned<T>::type U;
U u = r - l, g = 15, w = 0;
if(g == u) return l + rand4();
if(g > u){
U eu = u + 1, s = g / eu, t = s * eu;
do{
w = rand4();
}while(w >= t);
w /= s;
} else {
U eg = g + 1, s = u / eg;
do{
w = rand((U)0, s) * eg + rand4();
}while(w >= u);
}
return l + w;
}
int C[10];
int main(){
for(int i = 0; i < 100000; ++i)
++C[rand(1, 10) - 1];
for(int i = 0; i < 10; ++ i)
std::cout << i + 1 << ":" << C[i] << std::endl;
return 0;
}
```
---
讲完了比较复杂的随机生成 $[a,b]$ 内整数的实现,生成 $[a,b)$ 内浮点数的实现则要简单很多。由于浮点数没有很麻烦的精度溢出的问题,又因为是实数,所以处理起来相当简单:
$$
\operatorname{rand}(a,b)=a+(b-a)\cdot \operatorname{rand}_0()
$$
其中 $\operatorname{rand}_0()$ 可以生成一个均匀随机的在 $[0,1)$ 内的实数。
在 $\verb!random!$ 库里还定义了一个函数 $\verb!generate_canonical!$,它能使用一个均匀随机位生成器 $G$ 生成 $[0,1)$ 内的实数。一种容易想到的生成 $[0,1)$ 内随机实数的方法是用 $G$ 生成一个随机无符号整数 $p$,然后让它除去 $G_{\max}-G_{\min}+1$。看起来很对,但这种做法生成的浮点数熵值不够(举个较为极端的例子:$G_{\max}-G_{\min}+1=10$,那么这种做法生成的随机数只能是 $\frac{0}{10},\frac{1}{10},\frac{2}{10},\cdots,\frac{9}{10}$)。解决办法也很简单。首先计算 $\mathrm{erange}=G_{\max}-G_{\min}+1$(转换成浮点数,就不用担心 $+1$ 后的溢出问题了),然后计算出该浮点数类型精度部分所用的二进制位的个数 $m$(换言之,就是表示科学计数法指数部分需要使用的二进制位的个数)。显然,每次调用 $G$ 可以让 $\log_2\mathrm{erange}$ 位具有较高的熵值。那么我们调用 $m/\log_2\mathrm{erange}$ 次即可。实现较为容易,不再赘述。
在 $\verb!random!$ 库里,$\verb!generate_canonical!$ 还被包装进了一个内置的类 $\verb!__detail::_Adaptor!$ 里,再基于此实现了 $\verb!uniform_real_distribution!$。
我们称值在 $[l,r)$ 内均匀随机的随机变量 $X$ 服从均匀分布。记作 $X\sim \mathrm{Unif}(l,r)$。
## 复杂的分布
### 柯西分布
柯西分布的概率密度函数和累计密度函数,分别为:
$$
\begin{aligned}
f(x;x_0,\gamma)&=\frac{1}{\pi}\left(\frac{\gamma}{(x-x_0)^2+\gamma^2}\right)\cr
F(x;x_0,\gamma)&=\frac{1}{\pi}\arctan\left(\frac{x-x_0}{\gamma}\right)+\frac{1}{2}
\end{aligned}
$$
看上去这些式子非常复杂。但实际上我们可以用**逆变换法**来解决这样一类问题:
>已知一个累积分布函数 $F(x)$,现在需要计算 $\zeta$,使得 $\zeta$ 的累积分布函数为 $F(x)$。那么我们设 $U\sim\mathrm{Unif}(0,1)$,$F(x)$ 的逆函数为 $F^{-1}(x)$。大胆猜测 $\zeta=F^{-1}(U)$。此时,
>$$P(\zeta<k)=P(F^{-1}(U)<k)=P(U<F(k))=F(k)$$
>这证明了按照这种方法求出来的 $\zeta$ 确实是符合 $F$ 的。
>
>$U$ 的一个观测值 $u$ 容易获得,因此只要求出 $F^{-1}(u)$,就能得到一个 $\zeta$ 的观测值。当然,有时候 $F^{-1}(u)$ 比较容易获得,有时候又不那么容易得到。对于后者是一些算法针对的重点。
对于柯西分布的累计密度函数,我们很容易求出 $F^{-1}(x;x_0,\gamma)$:
$$
\begin{aligned}
y&=\frac{1}{\pi}\arctan\left(\frac{x-x_0}{\gamma}\right)+\frac{1}{2} \cr
\pi\left(y-\frac{1}{2}\right)&=\arctan\left(\frac{x-x_0}{\gamma}\right) \cr
x&=x_0+\gamma\cdot\tan\left(\left(y-\frac{1}{2}\right)\pi\right) \cr
F^{-1}(x;x_0,\gamma)&=x_0+\gamma\cdot \tan\left(\left(x-\frac{1}{2}\right)\pi\right)
\end{aligned}
$$
于是,只要在 $\mathrm{Unif}(-0.5,0.5)$ 里观测一个点 $x$,接着带入即可。
### 指数分布
我们用 $\mathrm{Exp}$ 表示指数分布。$\mathrm{Exp}(\lambda)$ 的概率密度函数被定义为 $f(x)=\lambda e^{-\lambda x}$。容易发现,
$$
\begin{aligned}
F(x)&=\int_{0}^xf(x)\mathrm dx=1-e^{-\lambda x} \cr
F^{-1}(x)&=-\frac{1}{\lambda}\ln(1-x)
\end{aligned}
$$
于是只要观测一个 $\mathrm{Unif}(0,1)$ 的随机变量 $x$,然后计算 $F^{-1}(x)$ 即可。
### 韦布尔分布
韦布尔分布的概率密度函数和累计密度函数,分别为:
$$
\begin{aligned}
f(x;\lambda,k)&=
\begin{cases}
\frac{k}{\lambda}(\frac{x}{\lambda})^{k-1}e^{-(x/\lambda)^k}&,x\ge 0\cr 0 &, x<0
\end{cases} \cr
F(x;\lambda,k)&=
\begin{cases}
1-e^{-(x/\lambda)^k} &,x\ge 0 \cr
0 & ,x<0
\end{cases}
\end{aligned}
$$
同样地,我们可以计算出累计密度函数的逆函数:
$$
F^{-1}(x;\lambda,k)=\lambda\cdot\sqrt[k]{-\ln(1-y)}
$$
于是只要观测一个 $\mathrm{Unif}(0,1)$ 的随机变量 $x$,然后计算 $F^{-1}(x)$ 即可。
### 极值分布
极值分布(这里是指其中的极小值分布)的概率密度函数和累计密度函数,分别为:
$$
\begin{aligned}
f(x)&=\frac{1}{\sigma}e^{\frac{x-\mu}{\sigma}-e^{\frac{x-\mu}{\sigma}}}\cr
F(x)&=1-e^{-e^{\frac{x-\mu}{\sigma}}}
\end{aligned}
$$
可能有点不大清楚。用 $\operatorname {exp}(x)$ 替代 $e^x$:
$$
\def\exp#1{\operatorname{exp}\left(#1\right)}
\begin{aligned}
f(x)&=\frac{1}{\sigma}\exp{\frac{x-\mu}{\sigma}-\exp{\frac{x-\mu}{\sigma}}}\cr
F(x)&=1-\exp{-\exp{\frac{x-\mu}{\sigma}}}
\end{aligned}
$$
同样地,我们可以求出它的逆函数:
$$
F^{-1}(x)=\mu+\sigma \ln(-\ln(1-x))
$$
于是只要观测一个 $\mathrm{Unif}(0,1)$ 的随机变量 $x$,然后计算 $F^{-1}(x)$ 即可。
### 伯努利分布
伯努利分布是一个非常简单的离散型概率分布。
$$
\begin{aligned}
P(X=0)&=p \cr
P(X=1)&=1-p
\end{aligned}
$$
那么我们观测一个 $\mathrm{Unif}(0,1)$ 的随机变量 $x$。如果 $x<p$,那就返回 $0$;否则返回 $1$。
### 几何分布
假如随机变量 $X$ 服从几何分布 $G(p)$,那么:
$$
P(X=k)=p\cdot (1-p)^k.k=0,1,2,\cdots
$$
考虑使用类似伯努利分布的方法,把每个 $k$ 的概率头尾相接画在数轴上。此时数轴上形成了一条长度为 $1$ 的线段 $[0,1)$。那么生成 $0$ 的概率对应 $[0,p)$,生成 $1$ 的概率对应 $[p,p+p(1-p))$,以此类推。在这条线段上任取一个点 $x_0$,然后判断它所在的线段对应哪个 $k$。我们设:
$$
g(k)=\sum_{i=0}^kP(X=i)=p\cdot \frac{(1-p)^{k+1}-1}{-p}=1-(1-p)^{k+1}
$$
根据最后一个式子,我们把 $g(x)$ 的定义域从自然数集扩域到非负实数集。然后考虑从 $1-(1-p)^{k+1}$ 反推出 $k$ 的值。
$$
\begin{aligned}
y&=1-(1-p)^{k+1} \cr
(1-p)^{k+1}&=1-y \cr
k+1&=\frac{\ln(1-y)}{\ln(1-p)} \cr
k&=\frac{\ln(1-y)}{\ln(1-p)}-1
\end{aligned}
$$
然后上取整,就能得到 $x_0$ 所在点对应线段的值。这其实仍然是逆变换法的应用。
---
到这里为止,我们计算的都是可以顺利计算出 $F^{-1}(x)$ 的分布。但有时候,并不那么容易计算出 $F^{-1}(x)$。
### 正态分布
对于一个符合正态分布的随机变量 $\zeta$ 而言,若 $\zeta\sim\mathcal N(\mu,\sigma^2)$,设 $\xi=\frac{\zeta-\mu}{\sigma}$,那么就有 $\zeta\sim\mathcal N(0,1)$。因此,只要能够生成服从标准正态分布的随机数,就可以得到服从 $\mathcal N(\mu,\sigma^2)$ 的随机数。
现在假设有两个变量 $X,Y$,它们都服从标准正态分布。于是有:
$$
X\sim\mathcal N(0,1)\Rightarrow f(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}\\
Y\sim\mathcal N(0,1)\Rightarrow f(y)=\frac{1}{\sqrt{2\pi}}e^{-\frac{y^2}{2}}\\
$$
$(x,y)$ 对应了平面直角坐标系上的一个点。于是,
$$
f(x,y)=f(x)f(y)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}\cdot \frac{1}{\sqrt{2\pi}}e^{-\frac{y^2}{2}}=\frac{1}{2\pi}e^{-\frac{x^2+y^2}{2}}
$$
现在我们用极角坐标的方式描述点 $(x,y)$。也就是用角度 $\theta$ 和该点到原点的距离 $r$ 描述 $(x,y)$。那么:
$$
\begin{aligned}
r&=\sqrt{x^2+y^2} \Rightarrow r^2=x^2+y^2 \cr
\theta&=\arctan(x\div y)
\end{aligned}
$$
并且我们硬点一下 $r$ 和 $\theta$ 对应的随机变量服从的分布:
$$
\begin{aligned}
r^2 &\sim \mathrm{Exp}\left(\frac{1}{2}\right) \cr
\theta & \sim \mathrm{Unif}(0,2\pi)=2\pi\mathrm{Unif}(0,1)
\end{aligned}
$$
设 $U\sim \mathrm{Unif}(0,1)$,于是 $R^2=-2\ln(1-U)$。这时候我们得到了一个非常简单地做法:
- 观测服从 $\mathrm{Unif}(0,1)$ 的随机变量,得到实数 $u_1,u_2$。
- 计算 $r=\sqrt{-2\ln(1-u_1)},\theta =2\pi u_2$。根据 $r$ 和 $\theta$ 作为极角坐标 $(r,\theta)$。
- 把 $(r,\theta)$ 转换为平面直角坐标系上的坐标 $(x,y)=(r\cos\theta,r\sin \theta)$。根据上面的反推,可以得到 $x,y$ 分别服从标准正态分布 $\mathcal N(0,1)$。
我们把该做法称为[$\textsf{Box-Muller transform}$](https://en.wikipedia.org/wiki/Box%E2%80%93Muller_transform)。
这种做法有个效率上的缺陷,就是计算 $\sin$ 和 $\cos$ 带来的时间开销。考虑换个角度,设 $X\sim \mathrm{Unif}(-1,1),Y\sim\mathrm{Unif}(-1,1)$,并分别进行观测,得到两个实数 $x,y$。如果 $(x,y)$ 不在单位圆里(或者在单位圆的圆心),那就直接排除并重新生成,直到符合要求。容易发现,此时的 $(x,y)$ 是在单位圆里均匀随机生成的一个点,设 $t=x^2+y^2$。考察由 $(x,y)$ 转换到极坐标的形式为 $(\theta',r')$,那么显然 $\theta'$ 对应的随机变量服从 $2\pi\mathrm{Unif}(0,1)$。此外,$t$ 对应的随机变量服从 $\mathrm{Unif}(0,1)$。又容易发现,
$$
\begin{aligned}
\cos \theta&=\frac{x}{r} \cr
\sin \theta&=\frac{y}{r}
\end{aligned}
$$
因此可以得到最终的式子:
$$
\begin{aligned}
x_0&=x\sqrt{\frac{-2\ln t}{t}}\cr
y_0&=y\sqrt{\frac{-2\ln t}{t}}
\end{aligned}
$$
$x_0,y_0$ 都是标准正态分布的观测值。优化后的做法称为 [$\textsf{Marsaglia polar method}$](https://en.wikipedia.org/wiki/Marsaglia_polar_method)。这里给出一个简单的实现:
```cpp
#include<iostream>
#include<cmath>
#include<random>
std::mt19937 MT;
double uni(){
return std::generate_canonical<double, 10>(MT);
}
double nod(){
static double rem; static bool flag = false;
if(flag){
flag = false; return rem;
}
double x, y, R;
do{
x = 2.0 * uni() - 1.0;
y = 2.0 * uni() - 1.0;
R = x * x + y * y;
}while(R == 0.0 || R > 1.0);
R = sqrt(-2.0 * std::log(R) / R);
rem = R * y, flag = true; return R * x;
}
const int MAXN = 20 + 3;
int C[MAXN], s, h = 20;
int main(){
for(int i = 0;i < 1000000; ++i){
double x = nod();
if(x < -2.5 || x > 2.5) continue;
++C[(int) round(x / 0.4) + 10];
}
for(int i = 0;i < 20; ++i)
s = std::max(s, C[i]);
for(int i = h - 1;i >= 0; --i){
for(int j = 0;j < 20; ++j)
std::cout <<(1.0 * C[j] / s * h >= 0.5 + i ? '*' : ' ');
std::cout << '\n';
}
return 0;
}
```
### 对数正态分布
根据定义,若 $X$ 服从对数正态分布,那么:
$$
\ln X\sim \mathcal N(\mu,\sigma^2)
$$
因此得出一个服从 $\mathcal N(\mu,\sigma^2)$ 的随机变量的观测值 $x_0$,然后返回 $e^{x_0}$ 即可。
### 伽马分布
在讲伽马分布前,我们讲一下**拒绝采样**法。
> 已知 $X$ 的概率密度函数 $f(x)$。考虑画出 $f(x)$ 的图像。容易发现,我们要做的实际就是在这条曲线下方的图形里**均匀随机**地任取一个点,然后取它的横坐标,这就是 $X$ 的一个观测值。
>
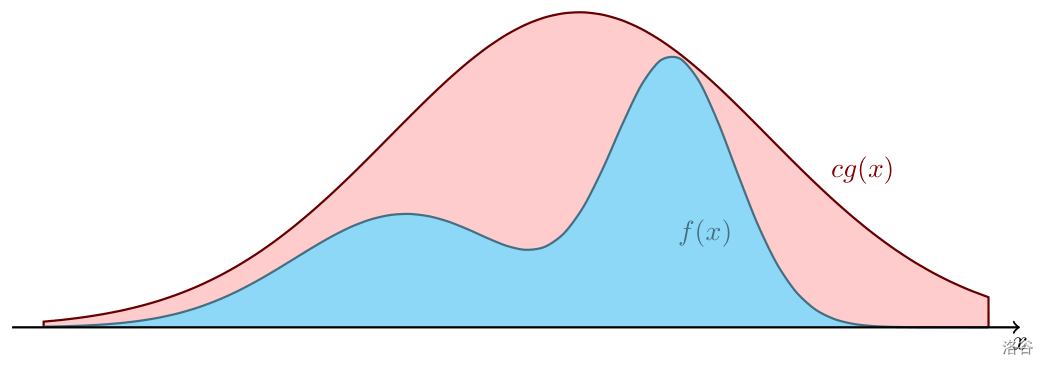
> 不过,有些函数图像下面的图形是不大容易随机取点的。考虑采取一种妥协的方法。对于概率密度函数 $f(x)$,我们找到另外一个随机变量 $Y$,它的概率密度函数 $g(x)$,累计密度函数为 $G(x)$。同时,存在一个常数 $c$,满足对于任意的 $x$ 都有 $cg(x)\ge f(x)$。现在我们观测 $Y$ 得到一个实数 $y$。但要注意的是,$g(y)\ge f(x)$,因此我们不一定接受这个 $y$。接受它的概率为:
> $$\frac{f(y)}{cg(y)}$$
> 如果被拒绝了,那就重新选定一个 $y$。直到接受了它,记 $x$ 为这个最终结果。按照这种做法最终获取的 $x$ 就是 $X$ 的一个合法的观测值。为了提高拒绝采样的效率,$g(x)$ 应当是**容易计算的**。并且 $\frac{f(x)}{cg(x)}$ 的值**越接近 $1$ 越好**。
>
> 
在 $\textsf{Marsaglia}$ 写的一篇期刊论文里,提出了一种 $\text{exact-approximation}$ 方法。大致如下:
>有时候我们无法快速计算 $F^{-1}(x)$ 的值。但是我们同样可以折中:选择一个 $g(x)$,它非常接近 $F^{-1}(x)$。但是 $g(U),U\sim\textrm{Unif}(0,1)$ 并不等于我们所需要的 $X$。但是可以考虑不使用 $U$,然是使用另外一个随机变量 $Y$ 来替代。那么,$Y$ 的概率密度函数应当为:
>$$h(x)=f(g(x))g'(x)$$
>这是容易证明的。因为,
>$$\begin{aligned}H(x)&=\int_0^x f(g(t))g'(t)\mathrm dt=F(g(x))\cr H^{-1}(x)&=g^{-1}(F^{-1}(x))\end{aligned}$$
>因而对于一个随机变量 $U\sim \mathrm{Unif}(0,1)$,有:
>$$g(H^{-1}(U))=g(g^{-1}(F^{-1}(U)))=F^{-1}(U)$$
讲完了前置芝士,现在来探讨一下伽马分布 $\Gamma(\alpha,\beta)$。它的概率密度函数如下:
$$
f(x;\alpha,\beta)=\frac{\beta^{\alpha}}{\Gamma(\alpha)}\cdot x^{\alpha-1}e^{-\beta x}
$$
有个性质:若 $X\sim \Gamma(\alpha,\beta),X_0\sim \Gamma(\alpha,1)$,那么 $X=\beta X_0$。于是只要能计算出 $X_0$ 的一个观测值,就能求出 $X$ 的一个观测值了。因此下文中,$\beta=1$。
然后我们着重讲一下 $\textrm{A Simple Method for Generating Gamma Variables}$。它构造了这样一个函数:
$$
h(x)=d(1+cx)^3 \\
d=\alpha-\frac{1}{3},c=\frac{1}{\sqrt{9d}}
$$
根据 $\text{exact-approximation}$ 方法,如果我们能找到一个 $X$,它的概率密度函数为
$$
g_0(x)=\frac{h(x)^{\alpha-1}\cdot e^{-h(x)}\cdot h'(x)}{\Gamma(\alpha)}
$$
并且设法得到了 $X$ 的观测值 $x$,就能通过 $Y=h(X)$ 得到服从 $\Gamma(\alpha,1)$ 的 $Y$ 的一个观测值 $h(x)$ 啦。现在考虑使用拒绝采样法观测 $X$。大胆设 $g(x)=\ln(g_0(x))$,这么做的好处是 $g(x)$ 的所有常数项**都可以忽略**,因为 $g(x)$ 上的一个常数因子在 $e^{g(x)}$ 里都会变成一个乘积,而拒绝采样法是可以忽略掉所乘上的数字的。
$$
\begin{aligned}
&\ln \frac{h(x)^{\alpha-1}\cdot e^{-h(x)}\cdot h'(x)}{\Gamma(\alpha)}\cr
\Rightarrow& (\alpha-1)\ln h(x)-h(x)+\ln h'(x)\cr
\Rightarrow& (\alpha-1)(3\ln(1+cx))+2c\ln(1+cx)-h(x)\cr
\Rightarrow& (\alpha-1/3)(3\ln(1+cx))-h(x)\cr
\Rightarrow& d(\ln(1+cx)^3)-h(x)+d
\end{aligned}
$$
取 $g(x)=d(\ln(1+cx)^3)-h(x)+d$,设 $g_0(x)=pe^{g(x)}$。同时,标准正态分布的概率密度函数也可以设为 $qe^{-0.5x^2}$。拒绝采样法的那个常数设为 $p/q$。那么接受一个用正态分布生成的 $x_0$,概率为:
$$
\frac{pe^{g(x_0)}}{\frac{p}{q}\cdot qe^{-0.5x^2}}=\frac{e^{g(x_0)}}{e^{-0.5x^2}}
$$
然后经过一番申必操作(论文里计算了一下 $e^{g(x)}$ 和 $e^{-0.5x^2}$ 的比例),可以发现 $e^{g(x)}$ 和 $e^{-0.5x^2}$ 非常接近!同时,可以证明 $e^{g(x)}\le e^{-0.5x^2}$。因而使用拒绝采样法可以得到一个效率很高的算法。基本框架如下:
- 根据标准正态分布生成随机数 $x$。
- 根据 $\mathrm{Unif}(0,1)$ 生成随机数 $u$,用来判断是否要接受这个 $x$。也就是计算 $u$ 和 $e^{g(x)+0.5x^2}$ 哪个更大。若前者更大,则拒绝;否则接受。
实际实现的时候,比较 $u$ 和 $e^{g(x)+0.5x^2}$ 可以先取对数变成 $\ln u$ 和 $g(x)+0.5x^2$。把后面的式子拆开来,并且设 $v=(1+cx)^3$,于是等价于比较 $\ln u$ 和 $d\ln v-dv+d$。尽管这种做法已经很快,它仍需要取两次对数。但有一种方法是,找到一个适合的函数 $s(x)$,满足 $s(x)\le e^{g(x)}\le e^{-0.5x^2}$。那么只要 $ue^{-0.5x^2}\le s(x)$ 时,就有 $u\le \frac{s(x)}{e^{-0.5x^2}}\le \frac{e^{g(x)}}{e^{-0.5x^2}}$,就接受 $x$。 论文里提到的 $s(x)$ 为:
$$
s(x)=(1-0.0331x^4)e^{-0.5x^2}
$$
指数部分是会被消去的。剩下来的部分容易计算。于是得到最终算法:
- 计算服从标准正态分布和 $\text{Unif}(0,1)$ 的两个随机数 $x,u$。同时计算 $v$,若 $v\le 0$ 就重新生成。
- 如果 $u\le (1-0.0331x^4)$,那就直接返回 $x$。否则:
- 如果 $\ln u\le d\ln v-dv+d$,那就返回 $x$。否则重新生成 $x,u$,直到符合要求。
然而并没有完全解决。这种做法在 $\alpha<1$ 时效率较低,因此需要利用 $\alpha+1$ 生成的随机数得到 $\alpha$ 的。将生成的随机数乘上 $\sqrt[\alpha+1]{u}$ 即可。
### 卡方分布
卡方分布 $\chi^2(n)$ 的概率密度函数如下:
$$
f(x;n)=\frac{x^{n/2-1}e^{-x/2}}{2^{n/2}\cdot \Gamma(n/2)}
$$
容易发现,这就是 $\alpha=\frac{n}{2},\beta =\frac{1}{2}$ 的伽马分布概率密度函数。于是直接套伽马分布就行了。
### 学生 t 分布
根据定义,假设 $X\sim\mathcal N(0,1),Y\sim \chi^2(n)$,那么服从学生 $t$ 分布 $t(n)$ 的 $Z$ 为:
$$
Z=\frac{X}{\sqrt{Y/n}}
$$
于是观测 $X,Y$ 得到 $x,y$,然后返回 $z=\frac{x}{\sqrt{y/n}}$ 即可。
### 费舍 F 分布
根据定义,假设 $X\sim\chi^2(n),Y\sim \chi^2(m)$,那么服从费舍 $F$ 分布 $F(n,m)$ 的 $Z$ 为:
$$
Z=\frac{X}{n}\div \frac{Y}{m}=\frac{X\cdot m}{Y\cdot n}
$$
同样地,观测 $X,Y$ 得到 $x,y$,然后返回 $\frac{xm}{yn}$。
### 二项分布
服从二项分布 $B(n,p)$ 的随机变量 $X$,满足:
$$
P(X=k)=\binom{n}{k}p^k(1-p)^{n-k}
$$
在 $\verb!random!$ 库里使用的是拒绝采样法(和另外一个解决小范围二项分布的做法)。但是我没能获取到相关论文以及里面的常数的来源(库里实现非常复杂),因此没办法讲解如何生成服从二项分布的随机数了。库里提供了这样的注释:
```cpp
/**
* A rejection algorithm when t * p >= 8 and a simple waiting time
* method - the second in the referenced book - otherwise.
* NB: The former is available only if _GLIBCXX_USE_C99_MATH_TR1
* is defined.
*
* Reference:
* Devroye, L. Non-Uniform Random Variates Generation. Springer-Verlag,
* New York, 1986, Ch. X, Sect. 4 (+ Errata!).
*/
```
### 泊松分布
服从泊松分布 $B(\lambda)$ 的随机变量 $X$,满足:
$$
P(X=k)=\frac{\lambda^k}{k!}e^{-\lambda}
$$
在 $\verb!random!$ 库里,使用的同样是拒绝采样法。然而我同样没能获取到相关函数及常数来源(与二项分布疑似出自同一本书),我就只能给出库中的注释了:
```cpp
/**
* A rejection algorithm when mean >= 12 and a simple method based
* upon the multiplication of uniform random variates otherwise.
* NB: The former is available only if _GLIBCXX_USE_C99_MATH_TR1
* is defined.
*
* Reference:
* Devroye, L. Non-Uniform Random Variates Generation. Springer-Verlag,
* New York, 1986, Ch. X, Sects. 3.3 & 3.4 (+ Errata!).
*/
```
### 负二项分布
服从负二项分布的随机变量 $X$,满足:
$$
P(X=k)=\left(\begin{array}{c}k+r-1\\r-1\end{array}\right)\cdot(1-p)^{k}p^{r}
$$
标准库里写到了这样一条注释:
```cpp
// This is Leger's algorithm, also in Devroye, Ch. X, Example 1.5.
```
同样因为过于生僻了,这里不做讲解。
### 采样分布
在经历了一大堆数学公式的洗礼后,本文将会以较为简单的采样分布作为结尾。
#### 离散分布
给定 $n$ 个实数 $w_{0},w_1,\cdots w_{n-1}$,其中 $w_i$ 表示数字 $i$ 的权重。定义服从该离散分布的随机变量 $X$,满足:
$$
P(X=i)=\frac{w_i}{\sum_{j=0}^{n-1} w_j}.i=0,1,\cdots (n-1)
$$
实现起来比较简单。计算 $S=w_0+w_1+\cdots+w_{n-1}$,然后让 $w_i$ 除去 $S$。此时每个数字的权重和就是 $1$ 了。**对其求前缀和**。在 $\textrm{Unif}(0,1)$ 内生成一个随机整数 $u$,然后在前缀和数组里二分出 $u$ 的位置并返回即可。
#### 分段常值分布
给定 $n$ 个实数 $b_0,b_1,\cdots b_{n-1}$ 作为分段函数的端点,同时给出 $n-1$ 个实数 $w_0,w_1,w_2\cdots w_{n-2}$,其中 $w_i$ 表示线段 $[b_i,b_{i+1})$ 的权重。该权重决定了最终生成的随机数应该在哪个线段上。概率密度函数为:
$$
f(x)=\frac{w_i}{\sum_{j=0}^{n-2}w_i(b_{i+1}-b_i)}.i=0,1,\cdots (n-1)
$$
更直观地,我们给出一个例子:
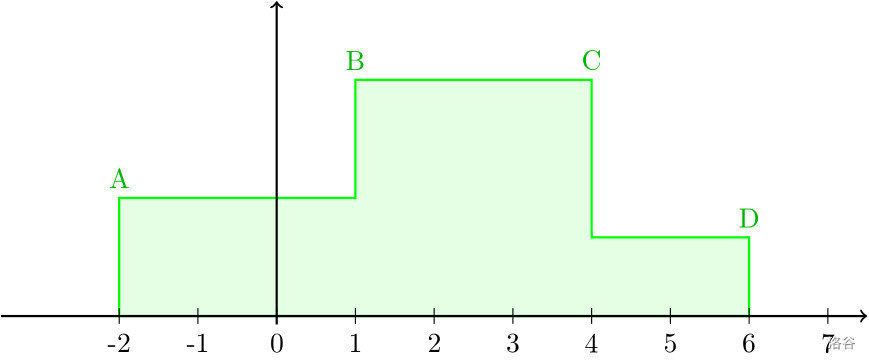
同样地,我们计算 $S=\sum_{j=0}^{n-2} w_j$ 并将每个 $w_i$ 除去 $S$,接着求 $w_i$ 的前缀和。同样地生成一个$\textrm{Unif}(0,1)$ 内的随机整数 $u$,并使用二分查找找到它所对应的那条线段。与离散分布不同的是,我们根据该条线段 $[w_x,w_{x+1})$ 上 $u$ 所在的具体位置,就可以得到随机出来的随机数,应该为:
$$
x=b_x+\frac{u-w_x}{w_{x+1}-w_x}\cdot(b_{x+1}-b_x)
$$
#### 分段线性分布
分段线性分布的定义要略微复杂一点。给定 $n$ 个实数 $b_0,b_1,\cdots b_{n-1}$ 作为分段函数的端点,同时给出 $n$ 个实数 $w_0,w_1,w_2\cdots w_{n-1}$,作为**每个端点的**权重。权重决定了该分布的概率密度函数在 $b_i$ 处的取值。它的概率密度函数并不算复杂,与分段常数分布有些许类似。以下是一个例子:
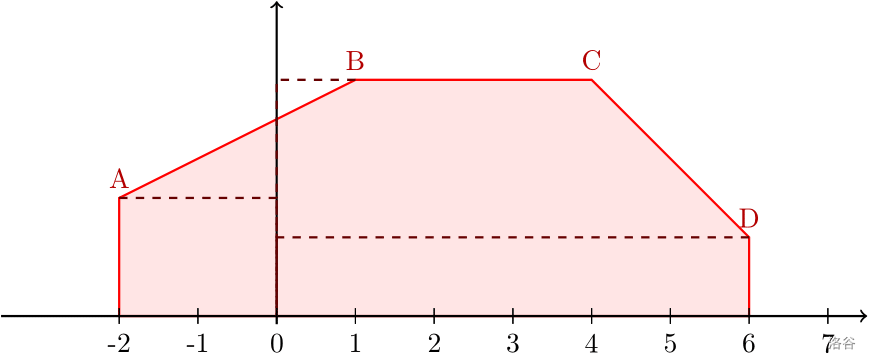
首先得计算出每个端点处的概率密度函数取值,使得整个图形的面积(粉红色部分)为 $1$。那么就得首先计算出原来的面积:
$$
S=\sum_{i=0}^{n-1}\frac{(b_{i+1}-b_i)\cdot (w_{i+1}+w_i)}{2}
$$
然后让每个 $w_i$ 除以 $S$,这样得到每个端点处的概率密度函数取值。接着我们就能计算出概率密度函数 $F(x)$ 在 $b_i$ 处的取值了。与前两个分布一样,我们在 $\mathrm{Unif}(0,1)$ 里随机出一个 $u$,二分 $u$ 应该在哪一段里面(设为 $[b_x,b_{x+1})$),接着计算出使得 $F(x)=u$ 的 $x$。
## 参考文献
- [$\text{如何向高斯分布中取样 how-to-sample-from-a-gaussian-distribution}$](https://www.alanzucconi.com/2015/09/16/how-to-sample-from-a-gaussian-distribution/)。
- [$\text{维基百科}$](https://en.wikipedia.org)。
- Devroye, L. Non-Uniform Random Variates Generation. Springer-Verlag, New York, 1986, Ch. X, Sects. 3.3 & 3.4 (+ Errata!)。
- Devroye, L. Non-Uniform Random Variates Generation. Springer-Verlag, New York, 1986, Ch. X, Sect. 4 (+ Errata!)。
- Marsaglia, G. and Tsang, W. W. "A Simple Method for Generating Gamma Variables" ACM Transactions on Mathematical Software, 26, 3, 363-372, 2000。