浅谈红黑树

## 浅谈红黑树 红黑树，是一种运用广泛，运行速度快的自平衡二叉查找树。 然而，由于其难度之大，码量之大，导致其在OI中的运用不如splay，treap等其他平衡树。 --- 前置芝士：二叉搜索树/平衡树 ### 0 说明 本文的部分变量/函数：$fa$ 父节点，$ch[0]/ ch[1]$ 左右子节点，$v$ 节点权值，$cnt$ 当前数的个数，$sz$ 子树中树的个数，$rt$ 根节点； $rnk$ 排名，$kth$ 排名为第 $k$ 的数，$suf$ 后缀，$pre$ 前驱，$ins$ 插入，$del$ 删除，$ins\_fix$ 插入修正（双红修正），$del\_fix$ 删除修正（双黑修正）。 由于我的个人习惯，本文所有变量不使用指针~~指针真的好丑啊~~。 ### 1 性质 - $1$ 一棵二叉搜索树，所有节点均为红色或黑色。 - 相信这一条性质无需多言了。 - $2$ 根节点为黑色。 - 根节点为黑色，会给我们后面的修正带来很大的便利。 - 另外，红黑树的黑高度变化全部在根节点产生，黑高度的定义在后文会有提及。 - $3$ 所有叶节点为黑色。 - 一般来说，我们会认为增加一层，也就是在叶节点的下放加一层 $0$ 节点，并令 $0$ 为黑色。 - 如果使用指针，那么就是叶节点的指针指向 $null$。 - $4$ 所有红节点的子节点均为黑节点。 - 这是一条保证红黑树复杂度的性质，使得每一个点到根节点的距离不超过黑高度的 $2$ 倍。 - $5$ 所有的叶节点到根节点的路径上的黑节点数量相同。 - 这一个数量也称就是黑高度。 - 由于存在这一条性质，我们可以保证每一个点到根节点路径上的黑点不超过 $\log n+1$。 那么到这里呢，红黑树的性质就讲完了。 由于第 $4$ 条性质和第 $5$ 条性质，我们可以保证任何一个点到根节点的距离不超过 $2\log n+1$，故复杂度有了保障。 另外还要说明一个结论：当一颗红黑树平衡时，其子树不违反除性质 $2$ 外的任何性质~~这不是显然的吗~~。 我们不妨称这样的子树是平衡的。 因此我们在后面的操作中只要保证子树平衡且黑高度不变，那么整颗红黑树不会违反除了 $4$ 之外的任何性质。 会违反 $4$ 的原因是子树的根节点可能是红的，而要是该节点的父节点可能也是红的。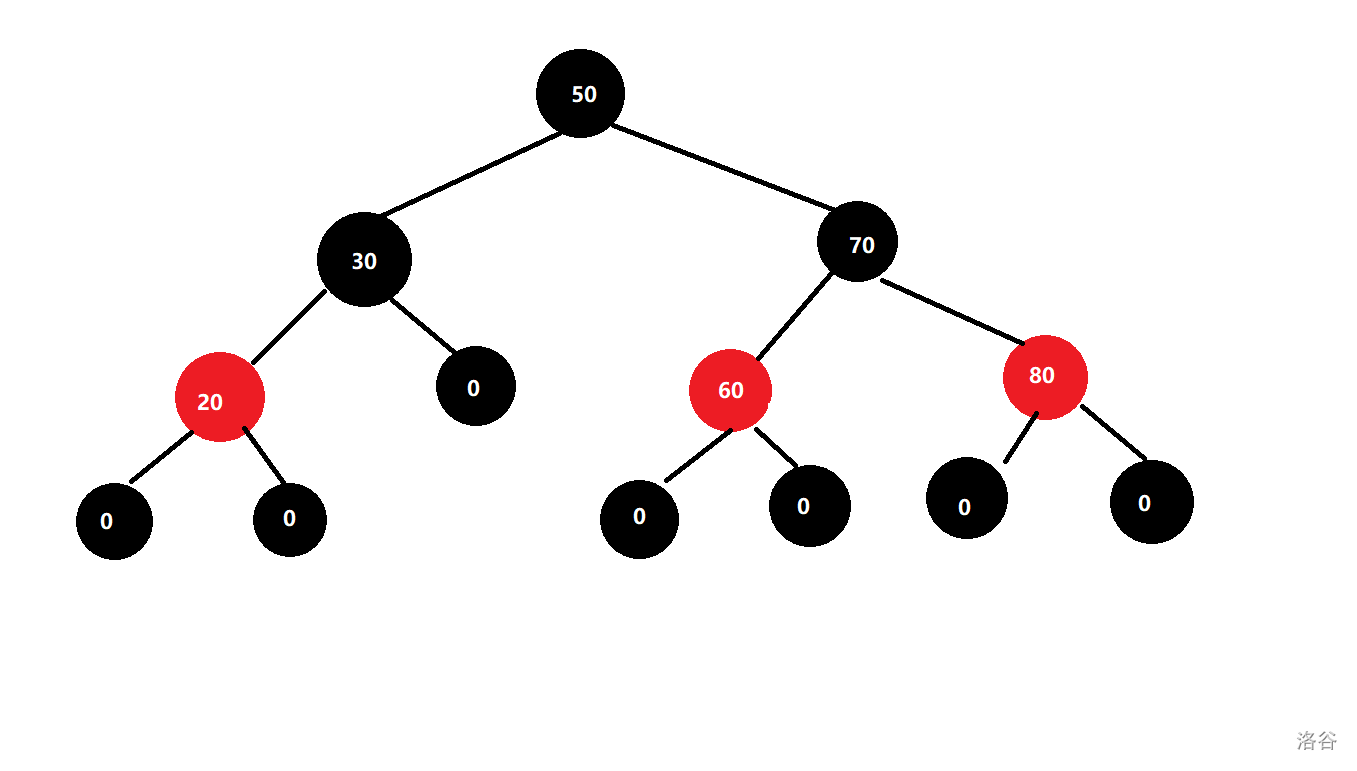 下面贴一副红黑树的图：  原谅我的绘图水平qaq ### 2 查询操作 由于红黑树是二叉查找树，故其满足二叉查找树的性质，查询方式与之相同。 在此不多加赘述，直接上代码。 ```cpp int kth(int k) { int tmp; int o=rt; for (;o;) { tmp=t[t[o].ch[0]].sz; if (tmp+1<=k&&k<=tmp+t[o].cnt) break; else{ if (k<=tmp) o=t[o].ch[0]; else{ k-=tmp+t[o].cnt; o=t[o].ch[1]; } } } return t[o].v; } int rnk(int v) { ins(v); int tmp=0,sum=0; int o=rt; for (;o;) { tmp=t[t[o].ch[0]].sz; if(v==t[o].v) break; else{ if(v<t[o].v) o=t[o].ch[0]; else{ sum+=tmp+t[o].cnt, o=t[o].ch[1]; } } } del(v); return sum+tmp+1; } int suf(int v) { int res=inf; int o=rt; for(;o;){ if(t[o].v>v){ res=t[o].v, o=t[o].ch[0]; } else o=t[o].ch[1]; } return res; } int pre(int v) { int res=-inf; int o=rt; for(;o;){ if(t[o].v<v){ res=t[o].v,o=t[o].ch[1]; } else o=t[o].ch[0]; } return res; } ``` ### 3 旋转操作 这一部分是修改操作的铺垫。 按照主流的说法，红黑树可以分为左旋和右旋；但其实这两者就是对称的形式。 旋转这一操作很难使用文字来描述，故在此放一张左旋的图片。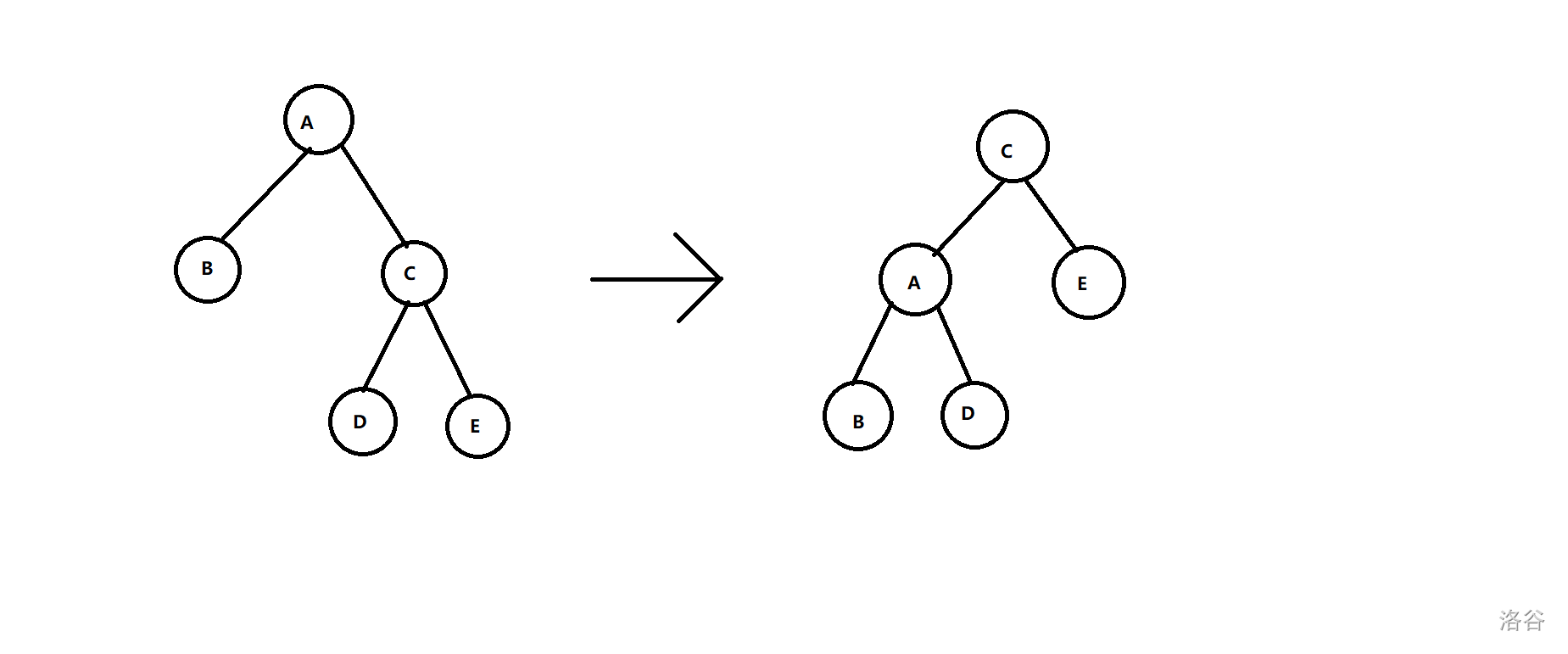 至于右旋，反过来就是了qaq  学过 splay 的同学也许会觉得和 splay 的旋转操作很像~~根本就是一模一样吗~~。 具体的操作呢，就是不断得赋值。注意赋值的先后，以防拿新值去更新。 ```cpp void pushup(int o){ t[o].sz=t[t[o].ch[0]].sz+t[t[o].ch[1]].sz+t[o].cnt; } bool get(int o){ return t[t[o].fa].ch[1]==o; } void rotate(int o,bool c){ int s1=t[o].ch[!c]; t[o].ch[!c]=t[s1].ch[c]; if (t[s1].ch[c]) t[t[s1].ch[c]].fa=o; t[s1].fa=t[o].fa; if(!t[o].fa) rt=s1; else t[t[o].fa].ch[get(o)]=s1; t[s1].ch[c]=o; t[o].fa=s1; pushup(o); pushup(s1); } ``` 这里的 $c$ 变量是用于判断左旋还是右旋的。特别要注意后面的 $pushup$ 的顺序。 --- 其实上面的部分都是基础操作，有一定平衡树基础的人甚至不需要学习。 而接下来的部分，才是红黑树真正令人智熄的操作~~其实也不难啦~~。 ### 4 插入操作 这一步操作也和二叉查找树相同~~为什么啥都一样啊~~。 进行查找，要是比当前节点小就进入左儿子，要是比当前节点大就进入右儿子。 直到找到一个和当前节点一样的点或是走到 $0$（也就是叶节点）位置。 然后如果走到了一个和当前节点一样的点，那就皆大欢喜了，我们只需要将 $cnt+1$ 就可以返回了。 要是走到 $0$ 节点，也就意味着当前红黑树中暂时没有这个点，我们需要新建一个节点。 然后这个时候我们就碰到问题了：新节点什么颜色？ 首先，如果当前的树是空树，那么显然是黑色。 如果新节点的父亲是黑色，那么这个点就是红色，因为在叶子上插入一个红节点不会影响黑高度。 要是父节点是红色的话。。。 无论如何，我都得违反一条红黑树的性质。（好像出大事情了qaq） 这个时候，我们就需要对这棵树进行修正。 我们修正的基本原则是：如果这一层能够解问题，那么我们直接解决。否则，我们交给父节点。 本着这样的思想，我们进行接下来的修正操作。 为方便起见，在此只讨论插入点在左边的情况，若是在右边则同理。 另外，由于目前最主流的写法在修正前会将该节点赋成红色，故在接下来的修改时，我先默认插入节点为红。 - $1$ 祖父节点的另一个子节点为黑色。 注意，如果没有另一个子节点我们也理解为黑色，因为没有该子节点就意味着指向 $0$。 然后我们发现，在这种大的情况下我们又有两种不同的情况。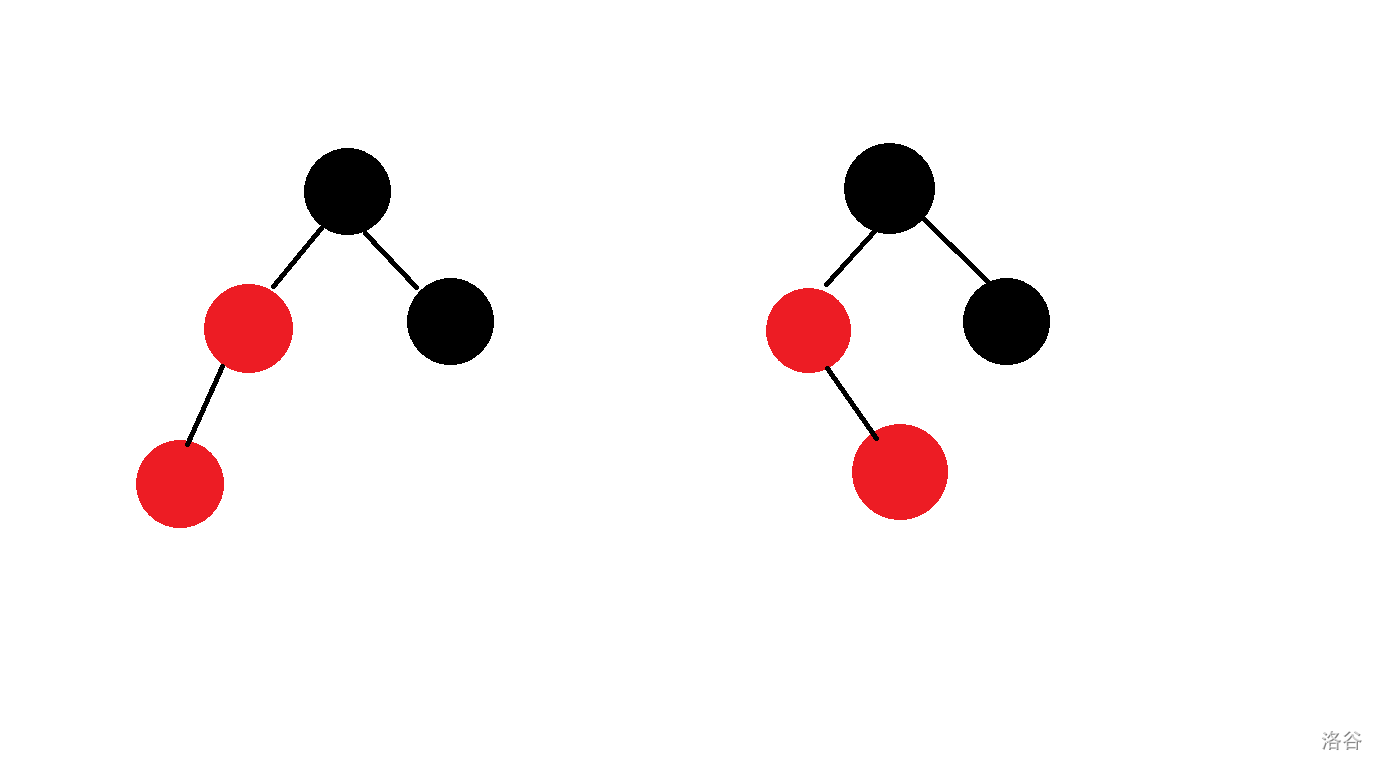  但实际上，这两种情况是一样的。如果我们出现的是右侧的情况，我们只需要进行一次左旋。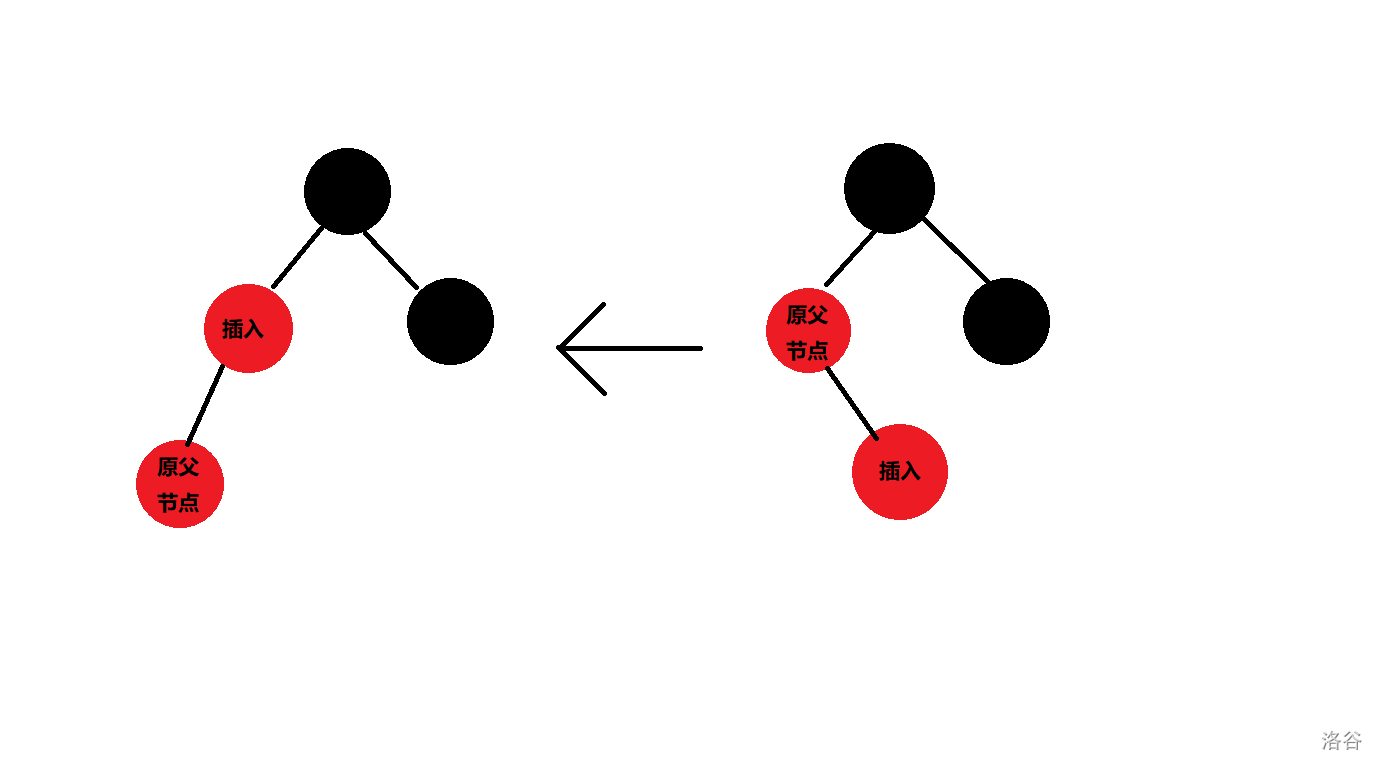  然后我们就化成了左侧的情况。对于这种情况，我们的处理方式是右旋后变色。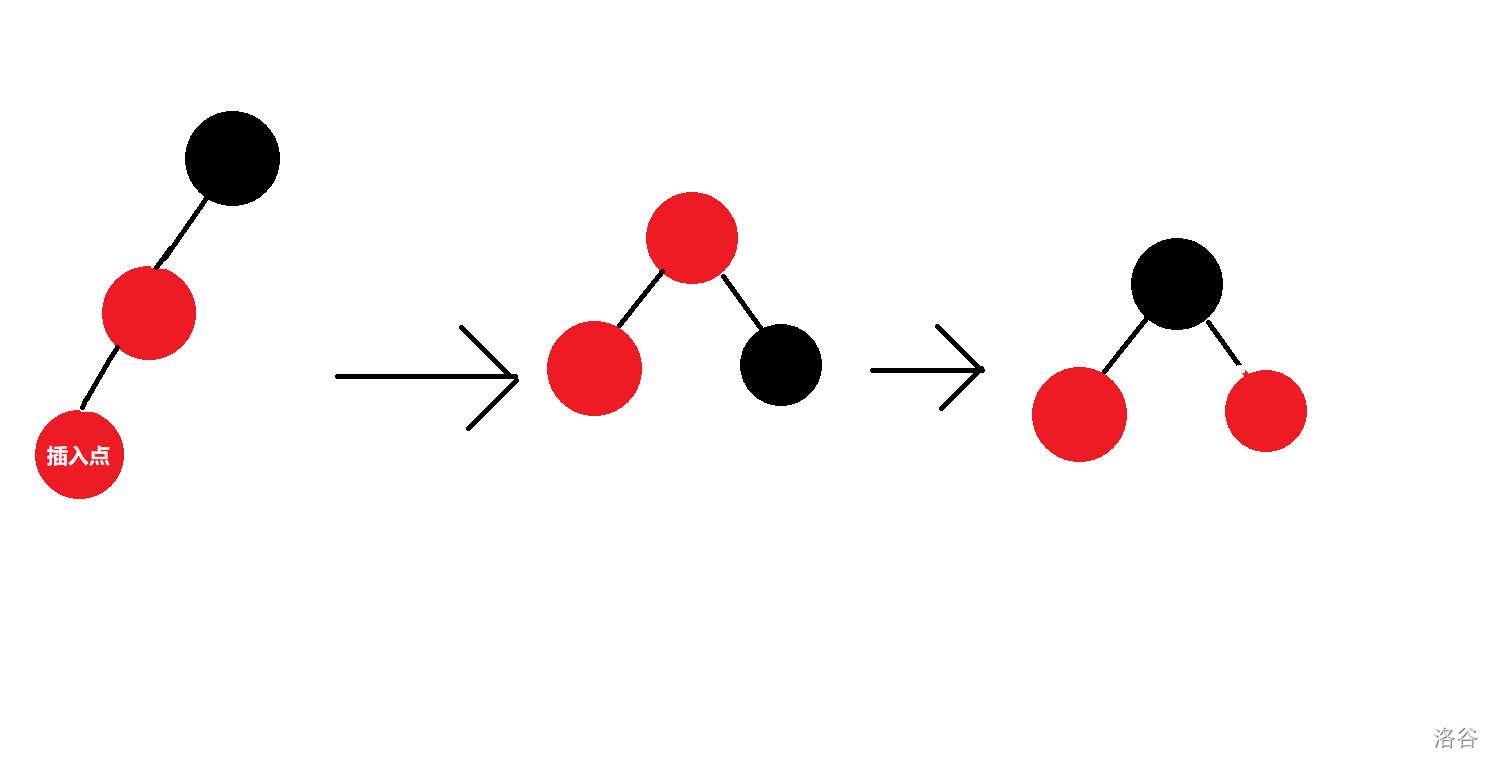  这样一来，两侧的黑高度都没有变化，就完成了子树的平衡。并且子树的根是黑节点，无需继续向上修改。 - $2$ 祖父节点的另一子节点也是红节点。 当我们碰到这种情况时，我们唯一能做的就是将父节点，祖父节点，祖父节点的另一个子节点反色。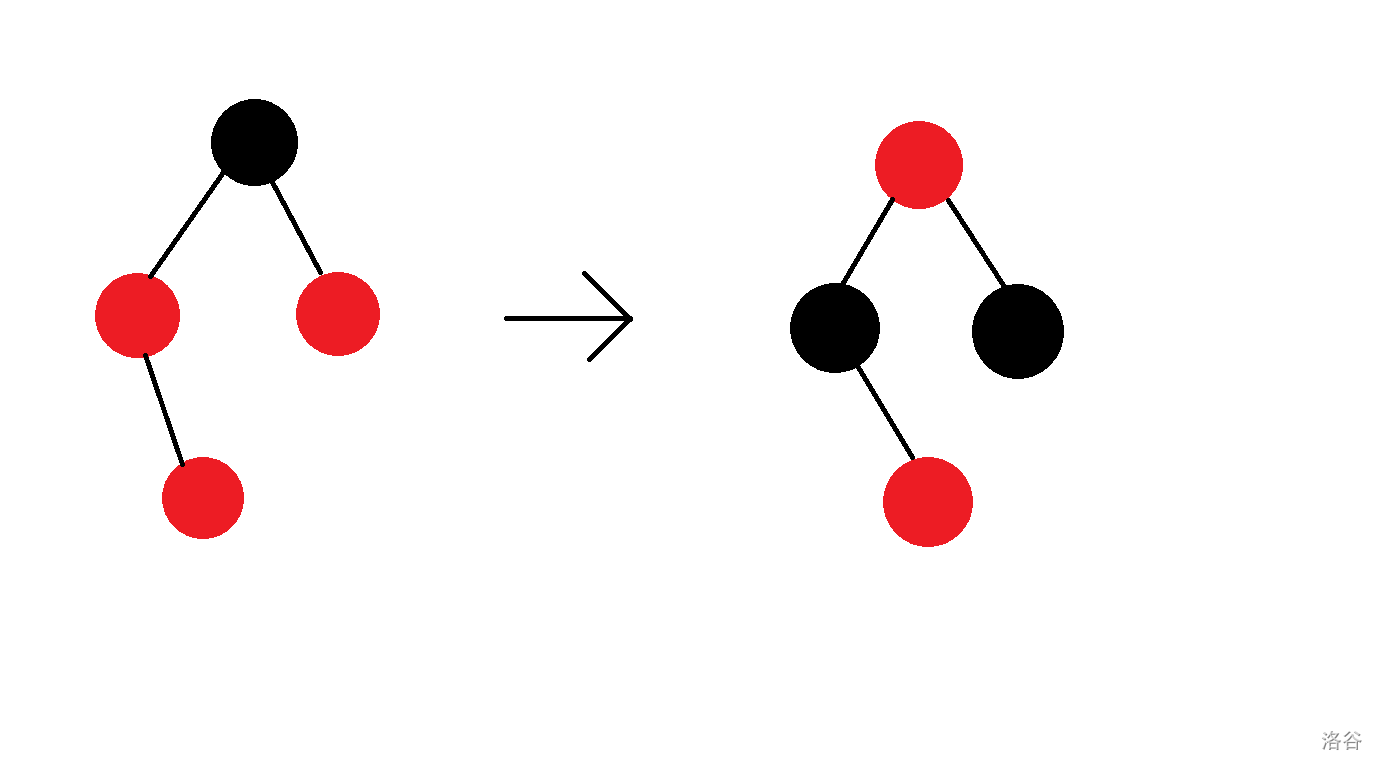 如图所示：  此时的插入点的位置就已经不重要了，不管是左还是右子树都平衡了。 但是由于祖父节点变红了，如果祖父的父亲也是红的，那么又冲突了。 这个时候我们发现，其实祖父节点也可以进行类似的讨论。 于是我们就可以层层向上递归，直到找到一个可以平衡的位置。 注意一下，如果在递归中的某一时刻根节点变红了，那么我们可以直接把根节点变黑，结束递归。 于是由于根节点的特殊性，保证了递归一定有出口。 同时，由于链长是 $\log$，故这样的递归最坏复杂度是 $\log$ 级别的。 ```cpp int newnode(int v){ int o=top?st[top--]:++tot; t[o]=(rbt){v,1,1,1,0,0,0}; return o; } void ins_fix(int o) { while(t[t[o].fa].col){ int f=t[o].fa,gf=t[f].fa; bool wh=!get(f); int ul=t[gf].ch[wh]; if(t[ul].col) { t[f].col=t[ul].col=0; t[gf].col=1; o=gf; } else{ if(o==t[f].ch[wh]) rotate(o=f,!wh); else{ t[gf].col=1; t[f].col=0; rotate(gf,wh); } } } t[rt].col=0; } void ins(int v) { int o=rt,f=0; while(o){ t[o].sz++,f=o; if(v==t[o].v){ t[o].cnt++; return; } o=t[o].ch[v>t[o].v]; } o=newnode(v); if(f) t[f].ch[v>t[f].v]=o; else rt=o; t[o].fa=f; ins_fix(o); } ``` 另外，由于我们是在碰到两个红节点相连的时候进行修正的，故这一修正操作又称为双红修正。 --- 然后我们细数一下，就剩一个删除操作了。 胜利就在眼前！ ~~其实感觉红黑树也不难啊~~ ### 5 删除操作 ~~继续同二叉搜索树~~ 首先，我们先找到我们需要删除的节点，然后看那个节点的 $cnt$。 如果 $cnt>1$ 直接 $cnt--$ 然后返回。 否则的话我们就要删除这个节点（然后就又出大事了qaq）。 而且这一次的情况比插入操作更为复杂，因为我们要删的节点不一定在叶子上。 然后我们又要分类讨论了。 受上面的启发，我们可以考虑将删除的节点转变成叶节点。 具体的操作是：如果删除的节点只有一个儿子，拿这个儿子替代这个点； 如果删除的节点有两个儿子，则用这个点的后缀来替代这个点。 如果后缀还有子节点，则拿那个子节点替代后缀的位置。 这个时候我们可能会违反以下二叉搜索树的性质。 不过没有关系，反正这个点快被删了。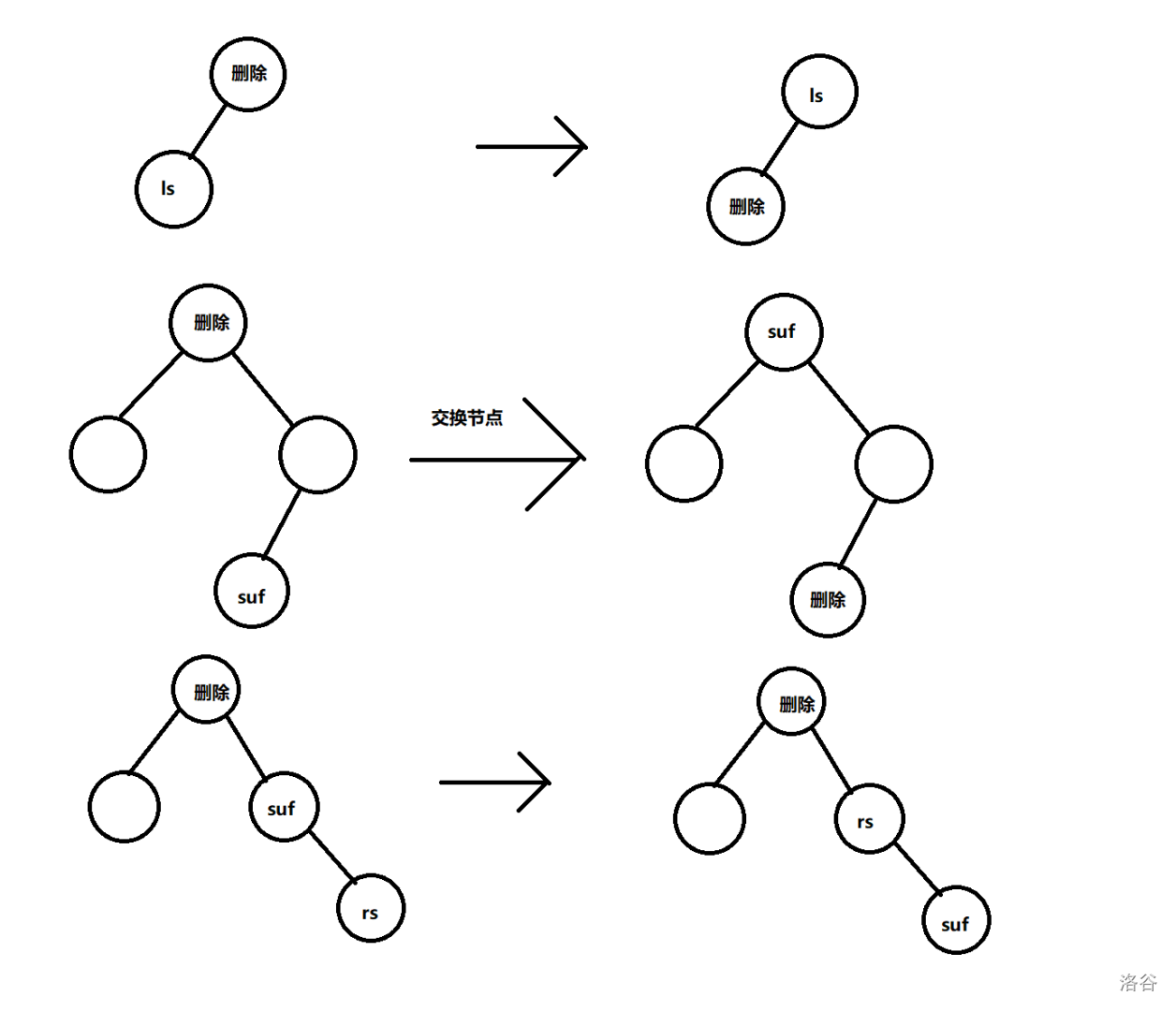  于是，经过上述操作，删除点全部变成了叶节点。 然后考虑如何修正。 同样的，在此只讲要删除的节点在左边的情况，右边的同理。 要是叶节点是红色，直接删除，并将其父亲的对应儿子变成 $0$。 要是当前节点是黑色，那我们要分情况。 注：当前节点（也就是我下面标"删除"的节点），并不是要直接删除，而是表明删除节点在其子树中。 被标明删除的点的子树已经平衡，并且其黑高度比未调整之前低 $1$。 另外，与双红修正相对，这种操作也别成为双黑修正。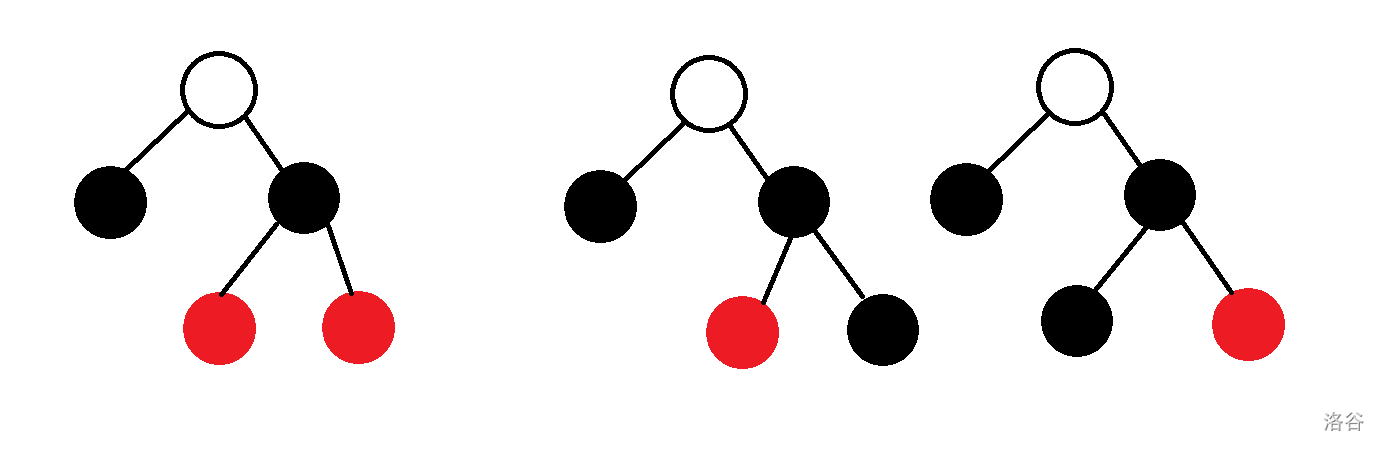 ~~然而我觉得这个称呼并不形象~~ - $1$ 父节点是黑色，其另一子节点是黑色，且这一节点的两个子节点至少有一个是红色  （空节点代表颜色任意） 如果出现的是第二种情况，我们先进行一次右旋和变色。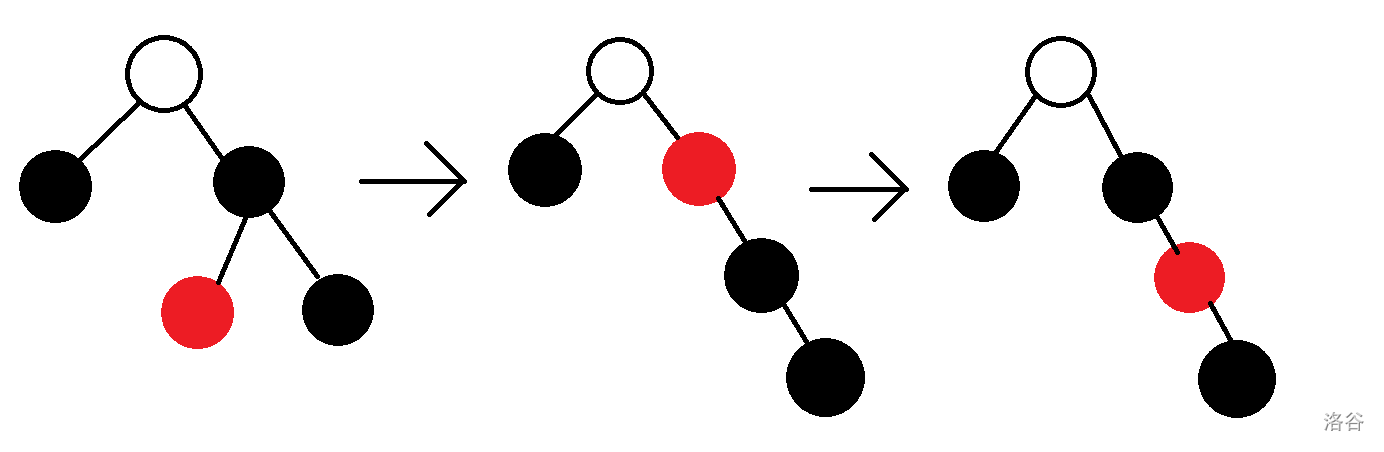  这样的好处就是，在三种情况中，父节点另一节点的右节点都是红色。 然后我们再进行一次旋转。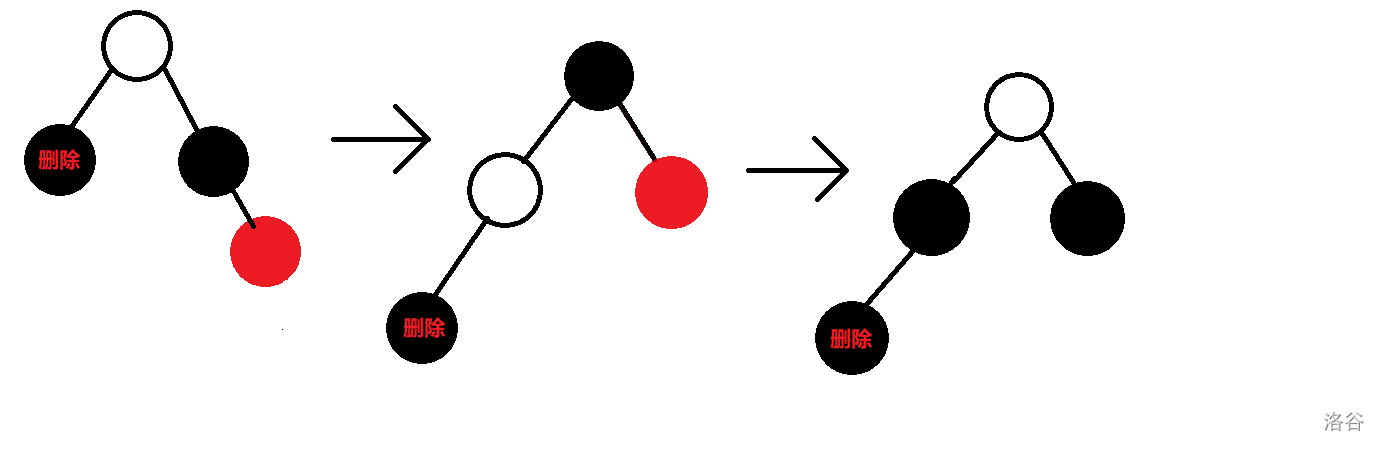  我们发现我们就完成了子树的平衡。于是，修正完成，返回。 - $2$ 祖父节点的另一子节点的两个儿子均为黑色 这种大情况下，又有两种不同的情况。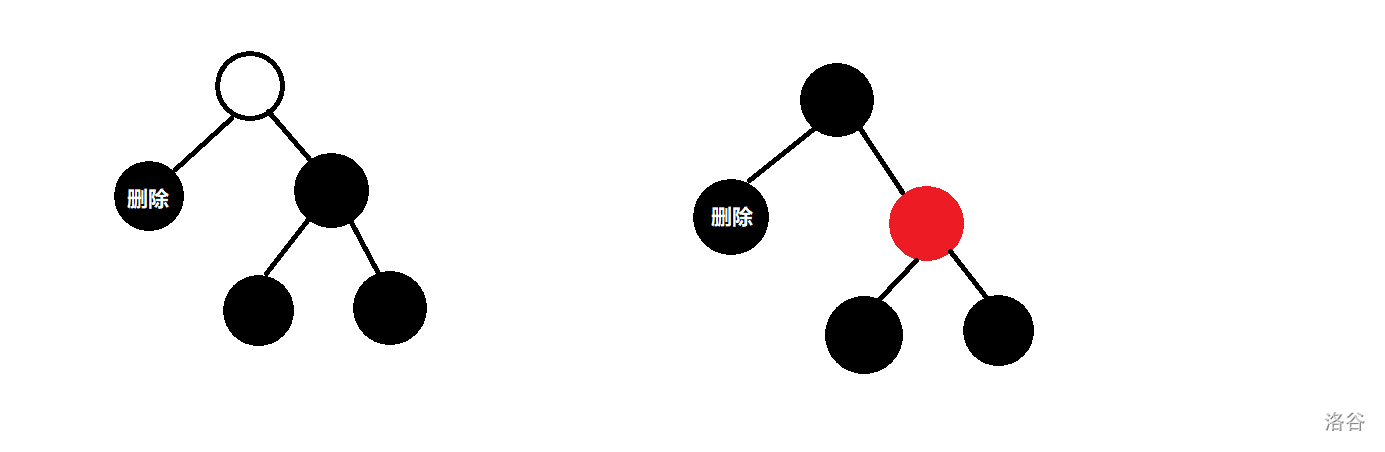  对于第一种情况，我们直接通过变色使右子树的黑高度减 $1$。 前面提到过，左子树的黑高度本来就低了 $1$，这样一来我们的子树又完成平衡了。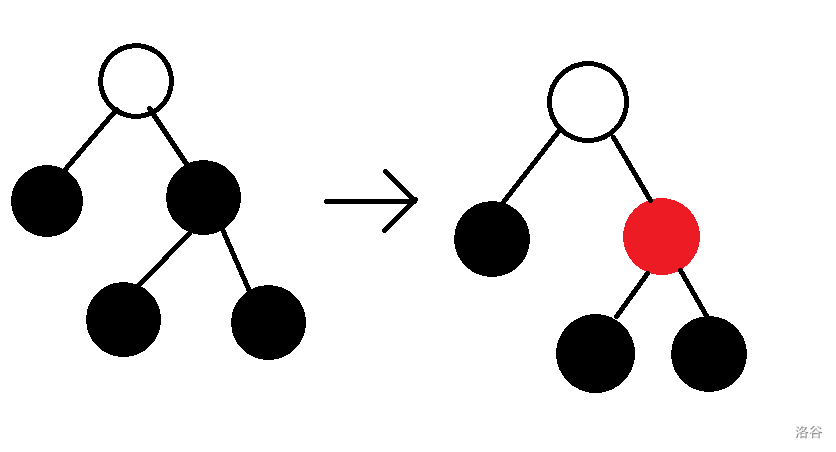  然后我们的再对父节点讨论： 如果父节点是红色，那么我们只要变成黑色就可以满足这棵子树黑高度与原来相同了； 如果父节点是黑色的话，我们发现这棵子树是平衡的，只是黑高度比原来低了 $1$。于是我们又可以向上递归。 对于第二种情况，我们发现这是唯一一种父亲的另一儿子是红色的情况 我们可以通过旋转和变色进行调整。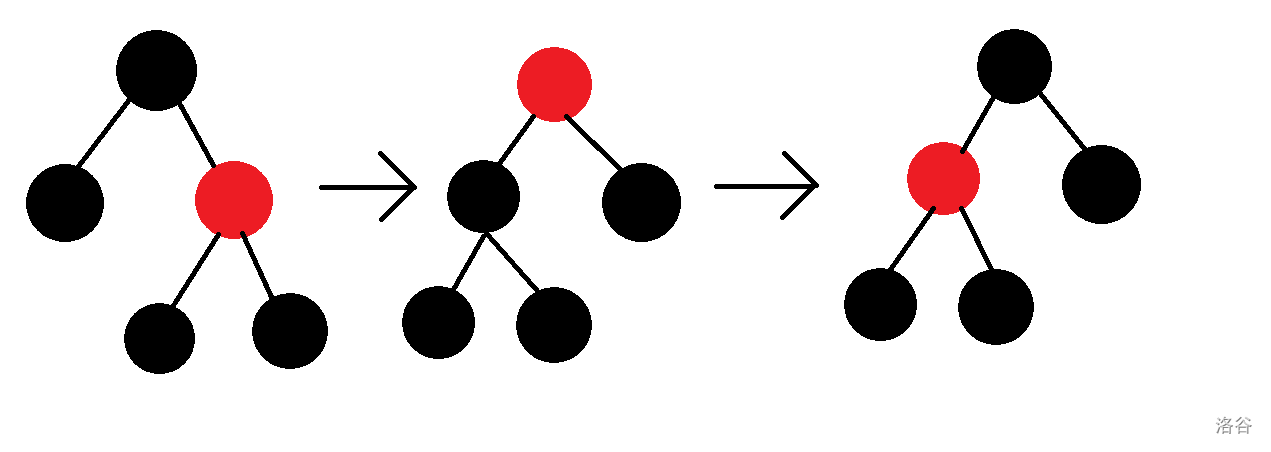  然后我们再把下面的子树拿出来重新讨论，发现这个时候被修改的节点的父亲的另一儿子变成了黑色。 于是我们再按照前面的几种操作递归。 于是我们可以一直递归上去直到某一时刻完成平衡。 这样就保证了我们的递归有出口，并且最多进行 $\log$ 次。 另外加一个小优化：我们用一个栈回收已经无效的节点，将其再利用以节省空间 ```cpp void del_fix(int o) { while(o!=rt&&!t[o].col) { bool wh=!get(o); int f=t[o].fa,ul=t[f].ch[wh]; if(t[ul].col){ t[ul].col=0; t[f].col=1; rotate(f,!wh); ul=t[f].ch[wh]; } else{ if(!t[t[ul].ch[0]].col&&!t[t[ul].ch[1]].col){ t[ul].col=1; o=f; } else{ if(!t[t[ul].ch[wh]].col){ t[t[ul].ch[!wh]].col=0; t[ul].col=1; rotate(ul,wh); ul=t[f].ch[wh]; } t[ul].col=t[f].col; t[t[ul].ch[wh]].col=t[f].col=0; rotate(f,!wh); break; } } } t[o].col=0; } void del(int v) { int o=rt; while(o&&t[o].v!=v){ o=t[o].ch[t[o].v<v]; } if(!o)return; if(t[o].cnt>1) { t[o].cnt--; update(o); return; } int d=o,g=0; if(t[o].ch[0]&&t[o].ch[1]){ d=t[o].ch[1]; while(t[d].ch[0]) d=t[d].ch[0]; } g=t[d].ch[!t[d].ch[0]]; t[g].fa=t[d].fa; if(!t[d].fa) rt=g; else t[t[d].fa].ch[get(d)]=g; if(o!=d){ t[o].v=t[d].v; t[o].cnt=t[d].cnt; } update(t[d].fa); for(int i=t[d].fa;i&&t[d].cnt>1&&i!=o;i=t[i].fa){ t[i].sz-=t[d].cnt; t[i].sz++; } if (!t[d].col) del_fix(g); st[++top]=d; } ``` 我们居然把红黑树给学完了！ ~~好像也不难啊~~ --- ### 6 总结 总的来说呢，红黑树比较考验代码能力，包括写代码的速度和细心程度（因为代码量比较大）。 但是不可否认的是红黑树的运行速度的确非常快，当 splay 选手还在与常数作斗争的时候，红黑树已经 AC。 因此，几种平衡树各有各的优点，不过对于 OI 来说也许 splay 和 treap 是更好的选择。 与 AVL 树相比的话，红黑树则是用了更劣的查询复杂度来换取了较好的修改复杂度（因为 AVL 的修改更加困难）。 另外，红黑树还有很多的用途，比如可以做文艺平衡树维护区间翻转，支持可持久化…… ~~只不过这些会使码量变得更大~~ 最后贴一个代码吧，肝了好久的qaq ```cpp #include <bits/stdc++.h> using namespace std; inline int read(){ register int x=0; register bool f=0; register char c=getchar(); while(c<'0'||c>'9'){ if(c=='-') f=1; c=getchar(); } while(c>='0'&&c<='9'){ x=(x<<3)+(x<<1)+c-48; c=getchar(); } return f?-x:x; } char cr[200];int tt; inline void print(int x,char k='\n') { if(!x) putchar('0'); if(x < 0) putchar('-'),x=-x; while(x) cr[++tt]=x%10+'0',x/=10; while(tt) putchar(cr[tt--]); putchar(k); } const int inf=2147483647; const int maxn=1100100; struct rbt{ int v,sz,cnt; bool col; int fa,ch[2]; }t[maxn*4]; int st[maxn*4],top,rt,tot,n,m,ans,lastans; void pushup(int o){ t[o].sz=t[t[o].ch[0]].sz+t[t[o].ch[1]].sz+t[o].cnt; } bool get(int o){ return t[t[o].fa].ch[1]==o; } int newnode(int v){ int o=top?st[top--]:++tot; t[o]=(rbt){v,1,1,1,0,0,0}; return o; } void rotate(int o,bool c){ int s1=t[o].ch[!c]; t[o].ch[!c]=t[s1].ch[c]; if (t[s1].ch[c]) t[t[s1].ch[c]].fa=o; t[s1].fa=t[o].fa; if(!t[o].fa) rt=s1; else t[t[o].fa].ch[get(o)]=s1; t[s1].ch[c]=o; t[o].fa=s1; pushup(o); pushup(s1); } void ins_fix(int o) { while(t[t[o].fa].col){ int f=t[o].fa,gf=t[f].fa; bool wh=!get(f); int ul=t[gf].ch[wh]; if(t[ul].col) { t[f].col=t[ul].col=0; t[gf].col=1; o=gf; } else{ if(o==t[f].ch[wh]) rotate(o=f,!wh); else{ t[gf].col=1; t[f].col=0; rotate(gf,wh); } } } t[rt].col=0; } void ins(int v) { int o=rt,f=0; while(o){ t[o].sz++,f=o; if(v==t[o].v){ t[o].cnt++; return; } o=t[o].ch[v>t[o].v]; } o=newnode(v); if(f) t[f].ch[v>t[f].v]=o; else rt=o; t[o].fa=f; ins_fix(o); } int kth(int k) { int tmp; int o=rt; for (;o;) { tmp=t[t[o].ch[0]].sz; if (tmp+1<=k&&k<=tmp+t[o].cnt) break; else{ if (k<=tmp) o=t[o].ch[0]; else{ k-=tmp+t[o].cnt; o=t[o].ch[1]; } } } return t[o].v; } void update(int o){ for(int i=o;i;i=t[i].fa){ t[i].sz--; } } void del_fix(int o) { while(o!=rt&&!t[o].col) { bool wh=!get(o); int f=t[o].fa,ul=t[f].ch[wh]; if(t[ul].col){ t[ul].col=0; t[f].col=1; rotate(f,!wh); ul=t[f].ch[wh]; } else{ if(!t[t[ul].ch[0]].col&&!t[t[ul].ch[1]].col){ t[ul].col=1; o=f; } else{ if(!t[t[ul].ch[wh]].col){ t[t[ul].ch[!wh]].col=0; t[ul].col=1; rotate(ul,wh); ul=t[f].ch[wh]; } t[ul].col=t[f].col; t[t[ul].ch[wh]].col=t[f].col=0; rotate(f,!wh); break; } } } t[o].col=0; } void del(int v) { int o=rt; while(o&&t[o].v!=v){ o=t[o].ch[t[o].v<v]; } if(!o)return; if(t[o].cnt>1) { t[o].cnt--; update(o); return; } int d=o,g=0; if(t[o].ch[0]&&t[o].ch[1]){ d=t[o].ch[1]; while(t[d].ch[0]) d=t[d].ch[0]; } g=t[d].ch[!t[d].ch[0]]; t[g].fa=t[d].fa; if(!t[d].fa) rt=g; else t[t[d].fa].ch[get(d)]=g; if(o!=d){ t[o].v=t[d].v; t[o].cnt=t[d].cnt; } update(t[d].fa); for(int i=t[d].fa;i&&t[d].cnt>1&&i!=o;i=t[i].fa){ t[i].sz-=t[d].cnt; t[i].sz++; } if (!t[d].col) del_fix(g); st[++top]=d; } int rnk(int v) { ins(v); int tmp=0,sum=0; int o=rt; for (;o;) { tmp=t[t[o].ch[0]].sz; if(v==t[o].v) break; else{ if(v<t[o].v) o=t[o].ch[0]; else{ sum+=tmp+t[o].cnt, o=t[o].ch[1]; } } } del(v); return sum+tmp+1; } int suf(int v) { int res=inf; int o=rt; for(;o;){ if(t[o].v>v){ res=t[o].v, o=t[o].ch[0]; } else o=t[o].ch[1]; } return res; } int pre(int v) { int res=-inf; int o=rt; for(;o;){ if(t[o].v<v){ res=t[o].v,o=t[o].ch[1]; } else o=t[o].ch[0]; } return res; } signed main(){ n=read();m=read(); for(int i=1;i<=n;i++){ int a=read(); ins(a); } while(m--){ int opt=read(),v=read()^lastans; if(opt==1) ins(v); if(opt==2) del(v); if(opt==3) lastans=rnk(v); if(opt==4) lastans=kth(v); if(opt==5) lastans=pre(v); if(opt==6) lastans=suf(v); if(opt!=1&&opt!=2)ans^=lastans; } print(ans); return 0; } ``` 希望能够帮到大家qaq