Updata 21/3/22:修了Latex和式子错误并且增添了一些补充的内容。
Updata 21/5/1:感谢 GuidingStar 在评论区指出问题,已更改。添加了5.的题外话内容。
前言
一切都只是我自己闲暇时研究的,这边写的本来仅仅当作我的一个小小的草稿纸,结果倒是写的挺详细的?
当然研究这个东西的原因最开始还是校内模拟赛的一道路径计数题,题解是 O(n^2) 的dp,但是我的同学当场用一个错误的思路写出来了一个 O(n) 的组合式子,而且AC了(orz),赛后他想了半天,感觉到处都不对,所以他就问了我,然后就引发了我的一堆思考,最终证明并优化,只剩下了一个组合数。
途中我也证明了许多有趣的结论,于是就在这里记录下来了。
0-1 本文讨论的范围
主要讨论的是在平面上的从一个点,到另一个点的路径方案等问题。
我去网上查了一些相关的文献,发现格路计数问题大部分都是用生成函数去推的,但是那样实在是无趣,所以本文主要是靠图象上的理解去推出答案的,可以放心食用。
当然,名字都是我自己乱起的,也定义了一坨自己的表示方法,说不定只看思路会更好?
虽然你会感觉这类问题比较的偏数学,但是有部分计数题目确实与这类结论有些关联(比如这种,好像关系也不算太大?),而且我在 4. 里面提出的一个算法看着也只能用计算机去计算结果,所以应该还是跟信息有很大关联的吧。
接下来就开始正题。
0-2 本文所用记号与定义
以下定义都是基于每次只能往右上或左下走这一条件的。
也就是说:当你处于 (x,y) 时,你只能走到 (x+1,y+1) 或 (x+1,y-1)。
-
我们认为一条路径与一条直线的相交次数就是有多少个整点既在路径上又在直线上。
-
一条路径与一条直线的不相交就是相交次数为 0,反过来相交就是相交次数不为 0。
-
组合数 \dbinom{n}{m}=C_n^m 也就是在 n 个物品中挑选 m 个的方案数。
-
记号 [a,b,c,d] 就是从 (a,b) 走到 (c,d) 的路径数。
-
记号 <a,b,c,d,k> 就是从 (a,b) 走到 (c,d) 且与直线 y=k 相交的路径数。
-
记号 \{a,b,c,d,k\} 就是从 (a,b) 走到 (c,d) 且与直线 y=k 不相交的路径数。
-
记号 [a,b,k] 就是从 (0,0) 走到 (a,b) 的所有路径与直线 y=k 相交次数之和。
-
记号 \left| a,b,k_1,k_2 \right| 就是从 (0,0) 走到 (a,b) 且与直线 y=k_1 和 y=k_2 都不相交的路径数。
-
记号 \left\langle\ a,b,k_1,k_2 \right\rangle 就是从 (0,0) 走到 (a,b) 且与直线 y=k_1 相交而与直线 y=k_2 不相交的路径数。
接下来罗列的是以下每一框求出来的结果。
1.
解得
### 2.
解得
$<a,b,c,d,k>=[a,b,c,2k-d]
\{a,b,c,d,k\}=[a,b,c,d]-[a,b,c,2k-d]
3.
解得当 0\le k\le b 时有
否则为
$\begin{aligned}[a,b,k]=\sum\limits_{i=\frac{a-b}{2}+k+1}^{a+1}\dbinom{a+1}{i}\end{aligned}$。
### 4.
解得
$\left| a,b,k_1,k_2 \right|=[0,0,a,b]-<0,0,a,b,k_2>-\left\langle\ a,b,k_1,k_2 \right\rangle
\left\langle\ a,b,k_1,k_2 \right\rangle =\left| a,2k_1-b,2k_1-k_2,k_2 \right| + \left\langle\ a,b,2k_1-k_2,k_2 \right\rangle
最后使用代码递归求解,复杂度 O(n)。
5.
给你一个括号序列 S。
你要在左右两头加上总共 n 个括号使整个括号序列合法。
求不同的方案数。
如果在左边添加上的括号序列为 A,在右边添加上的括号序列为 B,则当两个方案中的 A 或 B 有一个不同时就视为不同。
将 S 可以配对的括号先配对掉,最后只剩下 a 个 ) 与 b 个 (,如下:
\begin{matrix}\underbrace{)))\cdots))}&\underbrace{(((\cdots((}\\a&b\end{matrix}
最后解得答案为 \dbinom{n+1}{\frac{n+a+b}{2}+1}
1.无限制下的路径条数
定义一条合法路径,只要它满足以下两条即可:
-
从 (a,b) 出发到 (c,d) 停下。
-
当你处于 (x,y) 时,你只能走到 (x+1,y+1) 或 (x+1,y-1)。
那么合法路径条数为 \dbinom{c-a}{\frac{c-a+d-b}{2}} 。
记为 [a,b,c,d] ,也就是说 [a,b,c,d]=\dbinom{c-a}{\frac{c-a+d-b}{2}}。
证明
考虑有 x 步是往右上走,有 y 步是往右下走。
那么\begin{cases}x+y=c-a\\b+x-y=d\end{cases},解得\begin{cases}x=\dfrac{c-a+d-b}{2}\\y=\dfrac{c-a+b-d}{2}\end{cases}。
考虑到总共 c-a 步,其中放入 x 个往右上走的,方案数就是\dbinom{c-a}{\frac{c-a+d-b}{2}}
2.有一条不可碰横线的计数
定义一条合法路径,它要满足以下几条:
-
从 (a,b) 出发到 (c,d) 停下。
-
当你处于 (x,y) 时,你只能走到 (x+1,y+1) 或 (x+1,y-1)。
-
路径与直线 y=k(k<b 且 k<d) 不能有任何交点。
那么合法路径条数为 [a,b,c,d]-[a,b,c,2k-d]。
记为 \{a,b,c,d,k\},也就是 \{a,b,c,d,k\}=[a,b,c,d]-[a,b,c,2k-d]。
当然为了方便,我们再记从 (a,b) 到 (c,d) 且必须经过直线 y=k 的路径数为 <a,b,c,d,k> 。
那么会有 <a,b,c,d,k>=[a,b,c,2k-d]。
证明
如图,把 (c,d) 关于 y=k 对称到 (c,2k-d) 。
那么考虑所有从 (a,b) 到 (c,2k-d) 的路线,可以发现一定与 y=k 有交点,取第一个交点出来,把之后的路线关于 y=k 对称一下就是到 (c,d) 的一个与 y=k 相交的路线(就是红线变绿线)。
容易发现这就是 <a,b,c,d,k> 。
当然更严谨的证明还要说所有与 y=k 相交的路径也能对应一条从 (a,b) 到 (c,2k-d) 的路径,从双射的角度证明他们是等价的。
所以 <a,b,c,d,k>=[a,b,c,2k-d] 。
然后就很好得知 \{a,b,c,d,k\}=[a,b,c,d]-[a,b,c,2k-d] 了。
题外话
这好像叫折线法,而且众所周知,卡特兰数就是 C_n=\{0,0,2n,0,-1\},那么化一下就有其通项 C_n=\dfrac{\binom{2n}{n}}{n+1}
3.与一条直线的相交次数之和
定义一条合法路径,它要满足以下几条:
-
从 (0,0) 出发到 (a,b) 停下,其中 a,b 为正整数。
-
当你处于 (x,y) 时,你只能走到 (x+1,y+1) 或 (x+1,y-1)。
(为了方便,起始点就定为了 (0,0) ,其他情况都可以等同过来。)
定义一条合法路径的权值为其与直线 y=k 相交的次数。
求所有合法路径的权值之和。
求解
那么这里开始可能就要顺着我的思路来讲了(毕竟之前都是些熟知的东西)。
首先把答案也用一个符号记录 [a,b,k] 。(这个要跟1.中的 [a,b,c,d] 区分一下)
然后上图。
如图要计算绿点的数量。
那么这看起来不是一个简单的组合数能表示的。
所以我们考虑缩小问题规模。
怎么做呢?
先计算最后一个绿点的出现次数。
其实就是路径条数,就是 res1=[0,0,a,b] 。
然后计算不是最后一个的绿点的出现次数。
也就是在这个点 (i,k) 之后再与直线 y=k 有交点。
式子:\begin{aligned}res2=\sum\limits_{i=0}^{a-1}[0,0,i,k]\times (<i+1,k+1,a,b,k>+<i+1,k-1,a,b,k>)\end{aligned}
为什么后面是一个奇怪的和呢?
还记不记得 <a,b,c,d,k> 计算的是与 y=k 有交点的路径数?
那么就是说直接 <i,k,a,b,k> 并不是“在这个点之后再与直线 y=k 有交点”的方案数。
所以要先从 (i,k) 走一步再求。
于是就列出了上面那个式子,然后继续化。
res2&=\sum\limits_{i=0}^a[0,0,i,k]\times (<i+1,k+1,a,b,k>+<i+1,k-1,a,b,k>)\\
&=\sum\limits_{i=0}^a[0,0,i,k]\times [i+1,k-1,a,b]\times 2\\
&=\sum\limits_{i=0}^a[0,0,i,k]\times [i,k,a-1,b+1]\times 2
\end{aligned}
第一步是因为把 2. 中的结论代入,可以发现这个加和的其实是一个东西,直接乘 2 就好了;
第二步就是十分简单的把先从 (i,k) 往前走一步换个方向考虑,改为先从 (a,b) 往回走一步,这样就是上面这个东西了。
接着我们可以发现 res2=2\times[a-1,b+1,k] !
为什么呢?
让我们看到求 [a,b,k] 第二种想法。
还是上面那图。
我们想,不去缩小规模,可以直接枚举每个绿点会出现在多少条路径中。
式子:\begin{aligned}[a,b,k]=\sum\limits_{i=0}^a[0,0,i,k]\times[i,k,a,b]\end{aligned}
意思十分的简单,从 (0,0) 到 (i,k) 再到 (a,b),就是经过 (i,k) 的所有路径了。
然后我们看到 \begin{aligned}res2=\sum\limits_{i=0}^a[0,0,i,k]\times [i,k,a-1,b+1]\times 2\end{aligned}
这是不是十分的像?
所以观察一下,我们就可以得到 res2=2\times[a-1,b+1,k]
结合 res1=[0,0,a,b],可得 [a,b,k]=res1+res2=[0,0,a,b]+2\times[a-1,b+1,k]
这样就可以缩小问题规模了!
为什么呢?
[a,b,k]=[0,0,a,b]+2\times[a-1,b+1,k]
看到 [a-1,b+1,k],它可以用上面的式子递归的去分解!
边界?
可以发现当 a<b 时,甚至无法走到 (a,b),所以 [a,b,k] 为零,以这个为边界即可。
然后只要不停分解就好了,可以得到一个十分完美的式子:
\begin{aligned}[a,b,k]=\sum\limits_{i=1}^a2^{a-i}\dbinom{i}{\frac{a+b}{2}}\end{aligned}
我们发现居然跟 k 无关!
其实这是因为我们保证了 y=k 处于两个点的纵坐标之间,而当 y=k 不在这两个点的纵坐标之间呢?
我们可以发现一个十分重要的事情,就是 res1 和 res2 不一样了!
具体个怎么不一样呢?
最后一个绿点的出现次数 res1 原本是直接走到 (a,b) 就好了,因为一定会碰到直线 y=k ,但是现在就不一样了。
事实上现在应有 res1=<0,0,a,b,k>=[0,0,a,2k-b] 。
同理的 res2 也会有点不一样,读者自己推一下可以发现 res2=2\times [a-1,b-1,k]。
这样 k 就会在式子中,最终会有:
\begin{aligned}[a,b,k]=\sum\limits_{i=1}^a2^{a-i}\dbinom{i}{\frac{a-b}{2}+k}\end{aligned}
其实直接考虑把 (a,b) 关于 y=k 对称到 (a,2k-b) 也能得到一样的式子。
上面这条式子还有一个十分重要的优化。
我们抽象一下,就是给你 n,m ,求 \begin{aligned}\sum\limits_{i=1}^{n}2^{n-i}\dbinom{i}{m}\end{aligned}
那么我们用组合数恒等式 \dbinom{n}{m}=\dbinom{n-1}{m-1}+\dbinom{n-1}{m} 化。
如图,相当于每次都往右下移动,系数除2,然后把最后一项1留下。
最后就是组合数的一行的后缀。
事实上就是 \begin{aligned}\sum\limits_{i=1}^{n}2^{n-i}\dbinom{i}{m}=\sum\limits_{i=m+1}^{n+1}\dbinom{n+1}{i}\end{aligned}。
组合数后缀和,这个东西用分块,查询 q 次可以做到 O(\dfrac{n^2}{B}+qB) ,B 为块的大小。
当然,这里有更快的做法。
这样这题到这就结束了。
题外话
当 y=k 处于两个点的纵坐标之间的时候答案居然会与 k 无关,这里我们想下这个性质可以怎么去理解。
我们只要证明无论 k 为多少,都与 k=0 的时候的答案是一样的就好了。
如图,我们假设路径最后与 y=k 的交点在 (i,k) 。
那么我们把从 (0,0) 到 (i,k) 的路径关于中心对称一下(红线变绿线)。
可以发现绿线与 y=0 相交的次数一定等于红线与 y=k 的相交次数,结论便得到了证明。
4.有两条不可碰横线的计数
定义一条合法路径,它要满足以下几条:
-
从 (0,0) 出发到 (a,b) 停下,其中 a,b 为正整数。
-
当你处于 (x,y) 时,你只能走到 (x+1,y+1) 或 (x+1,y-1)。
-
路径与直线 y=k_1(k_1<0) 和直线 y=k_2(k_2>b) 都不能有任何交点。
求合法路径数。
-10^6\le k_1<0<b<k_2\le10^6,0\le a\le10^6
求解
读者可以先自己尝试求一下,毕竟可以用一个 O(n^2) 的dp来对拍。
虽然 2. 与这个十分的相似,一个是一条线,一个是两条线,
但是马上就可以发现,这个东西的求解难度 2. 无法与其相比。
先对称?那沿一条线对称后另一条线怎么办?
考虑信息学办法,把dp方程用矩阵优化?
看着都不太行的样子,没办法,只好硬着头皮上了。
考虑把所有不合法的算出来。
把不合法的路线分为碰到 y=k_2 的或不碰到 y=k_2 而碰到 y=k_3 的两种。
我们先把所有一定碰到 y=k_2 的算出来: res1=<0,0,a,b,k_2>,
然后让我们关于 y=k_1 对称一下。
如图,第一个交点是 (i,k_1) ,后面的红线与原来的绿线对称,y=k_2 被对称为 y=k_3=2k_1-k_2,(a,b) 被对称为 (a,2k_1-b)。
然后我们算经过 y=k_1 而不经 y=k_2 的方案,
可以发现,这要对称前的红线不碰到 y=k_2 和 y=k_1 ,对称点之后的红线不碰到 y=k_3 才行。
这没办法算啊,算前半部分的时候还要递归!
然后我就天真的在打表,对称,相交次数中反复横跳,想了好久怎么算,但是都没法做。
但是,当我同 3. 中一样,考虑如何不断缩小问题规模后,终于是找到了一种 O(n) 的偏信息学的办法!
读到此处的读者可以停下来想一想,如何才能像 3. 一样,缩小问题规模呢?说不定你可以找到一种全新的办法。
当然我的想法也十分的有思维难度。
让我们先进行一波定义:
$\left\langle\ a,b,k_1,k_2 \right\rangle$ 表示从 $(0,0)$ 走到 $(a,b)$ 且**必须碰到 $y=k_1$ 而不能碰到 $y=k_2$** 的路径数。
那么我们现在要求 $\left\langle\ a,b,k_1,k_2 \right\rangle$ 。
而且已经可以得到 $\left| a,b,k_1,k_2 \right|=[0,0,a,b]-<0,0,a,b,k_2>-\left\langle\ a,b,k_1,k_2 \right\rangle
(就是所有路线中减去不合法的)
然后让我们看到,\left| a,2k_1-b,k_3,k_2 \right| 是个什么东西?
还是上面那图。
我们看到这样的路径一定是可以算到我们想求的 $\left\langle\ a,b,k_1,k_2 \right\rangle$ 中的。
但是少算了什么呢?
我们看到要求:“**对称前的红线不碰到 $y=k_2$ 和 $y=k_1$ ,对称点之后的红线不碰到 $y=k_3$ 才行**”
也就是说**对称点之后的红线碰到 $y=k_2$ 是可以的!**
而我们直接让这条红线无论如何都不能碰到 $y=k_2$ 了!
所以少算了许多。
那么怎么加回来呢?
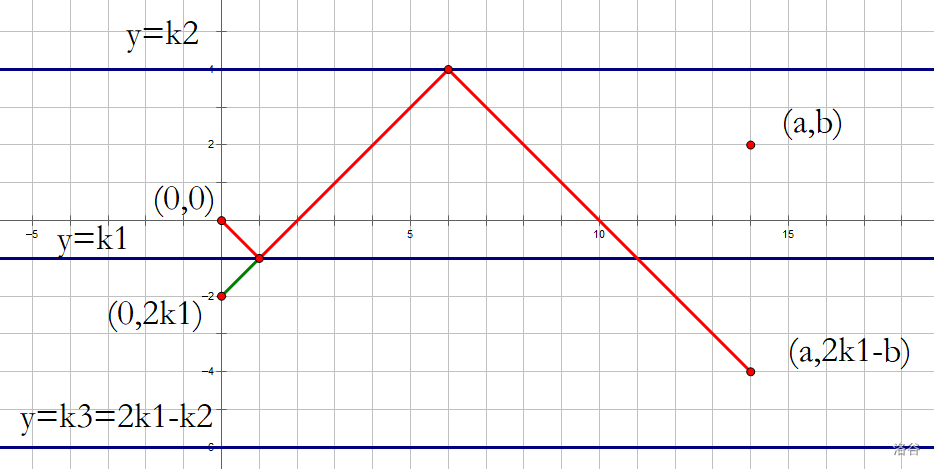
看到这条被我们漏了的红线。
我们想,它一定会先与直线 $y=k_1$ 相交,然后跟 $y=k_2$ 相交。
那么把 $(0,0)$ 也对称下来到 $(0,2k_1)$ 。
一条从 $(0,2k_1)$ 到 $(a,2k_1-b)$ 且**不能经过 $y=k_3$ 而必须经过 $y=k_2$ 的**路线,是不是就对应着所有被我们漏算的方案呢?
是的!
因为如图所示的绿线,在对称前不会经过 $y=k_3$ ,恰好就代表了对称后它不会经过 $y=k_2$ ;当它与 $y=k_2$ 相交之前,恰好一定会与 $y=k_1$ 有至少一个交点,所有的东西都对上了!
当然了,我们其实与其把 $(0,0)$ 对称下去,还不如把其他东西对称回来,所以就变成了:一条从 $(0,0)$ 到 $(a,b)$ 且**不能经过 $y=k_2$ 而必须经过 $y=k_3$ 的**路线。
那么我们就得到了一个递归的求解式子!
$\left| a,b,k_1,k_2 \right|=[0,0,a,b]-<0,0,a,b,k_2>-\left\langle\ a,b,k_1,k_2 \right\rangle
\left\langle\ a,b,k_1,k_2 \right\rangle =\left| a,2k_1-b,2k_1-k_2,k_2 \right| + \left\langle\ a,b,2k_1-k_2,k_2 \right\rangle
然后为什么这个把问题规模缩小了呢?
考虑到两条直线间的距离每次都会扩大两倍,而直线太远的时候我们就可以不去考虑直线的影响!
所以如果我们无论怎么走都无法碰到 y=k_1 时就可以直接停止递归。
代码如下:
ll mul[N],inv[N],MOD=998244353;//mul是前缀积,inv是mul的逆元
ll solve1(ll a,ll b,ll k1,ll k2);
ll C(ll x,ll y)//x中选y个
{
if(y>x)return 0;
return mul[x]*inv[y]%MOD*inv[x-y]%MOD;
}
ll walk(ll a,ll b,ll c,ll d)//从(a,b)走到(c,d)
{
if((c-a+d-b)&1)return 0;
if(d-b>c-a||b-d>c-a)return 0;
return C(c-a,(c-a+d-b)/2);
}
ll solve0(ll a,ll b,ll k1,ll k2)//不能碰y=k1和y=k2
{
if(a<-b||a<b)return 0;
return (walk(0,0,a,b)-walk(0,0,a,2*k2-b)-solve1(a,b,k1,k2)+MOD+MOD)%MOD;
}
ll solve1(ll a,ll b,ll k1,ll k2)//必须碰y=k1而不能碰y=k2
{
if(a<-b||a<b)return 0;
if(a<2*k1-b||a<b-2*k1)return 0;
return (solve0(a,2*k1-b,2*k1-k2,k2)+solve1(a,b,2*k1-k2,k2))%MOD;
}
预计复杂度 O(n) (因为每次往下递归计算2个,总共递归logn层,同线段树一样,最后会有n次计算),实测这部分会略快于 O(n),因为当直线间的距离越大,计算越快,而距离太小的时候一般可以直接dp,这两个做法速度恰好反着的。当然还是少不了前缀积的预处理 O(n) 的复杂度。
题外话
说不定可以用这个代码计算最终答案可以用哪些组合数表示,然后找出一个更优的式子,毕竟所有组合数都在同一行。当然,这就留给有心人去做了。
5.有额外走法的情况
其实网上有很多这方面的问题,然后就有Schröder数,Delannoy数,Motzkin数,Narayana数,Hipparchus数什么的。
不过我也不可能拿那些东西来讲吧,所以让我们来看到一个我所要做的最一开始的问题(也就是前言里说的)。
给你一个括号序列 S。
你要在左右两头加上总共 n 个括号使整个括号序列合法。
求不同的方案数。
如果在左边添加上的括号序列为 A,在右边添加上的括号序列为 B,则当两个方案中的 A 或 B 有一个不同时就视为不同。
可以发现,你把左括号看作向右上走,右括号看作向右下走。
那么你要满足最终走到 y=0 ,而且始终不能走到x轴下方,也就是不能碰到 y=-1。
所以按题目给你的括号序列走一遍,记录下走到的最低点以及终点的纵坐标 -k,-b 。
假如把这个题目给你的括号序列走过的总过程直接抽象成一个“传送”!
那不就是要“传送”前纵坐标不小于 k ,然后向下移动 b 步吗。
总得来看,就是:
有个人要从 (0,0) 去 (a,0) (为了方便令 a=n 了)。
假设他现在处于 (x,y) ,那么他有三种行走的方式:
-
走一步到 (x+1,y+1) 。
-
走一步到 (x+1,y-1) 。
-
满足 y\ge k ,那么可以传送到 (x,y-b) 。
不过他只会且一定会进行一次传送。
而且始终不能与 y=-1 相交。
定义路径不同为有某个时刻的行走方式不同。
给定 a,b,k ,保证 b\le k 且 a,k 为非负整数。
求不同的路径数。
求解
答案就是 \dbinom{a+1}{\frac{a-b}{2}+k+1},下面一步步证明为什么。
首先我们考虑与其是人传送下去,不如看作是终点传送上来,那么要求的其实就是这样一个问题:
从 (0,0) 走到 (a,b) ,对于一个路径,定义它的可传送点的个数为满足以下两条的 (x,y) 的数量:
-
-
在 (x,y) 之后路径上的所有点都在直线 y=b-1 之上。因为原来传送后还是不能碰到 y=-1,既然现在把所有东西都看作上移了 b,那么就变成不能碰到直线 y=b-1 了。
比如图中这条,黄点虽然在 y=k 之上,但是不能算,因为后面有个黑点碰到了 y=b-1 ,而绿点都是可以选的。
然后只要求所有路径的可传送点数量的和就好了。
但是这只能做到 O(n^2) 啊 (当然 O(n^2) 都难)
不急,我们慢慢来。
我们首先给出一个结论:
答案 = \sum\limits_{i=0}^{a} [ 从 (0,0) 到 (i,k) 的方案 ] \times [ (i,k) 到 (a,b) 且不碰直线 y=b-1 的方案 ]
也就是 \begin{aligned}ans=\sum\limits_{i=0}^{a}[0,0,i,k]\times \{i,k,a,b,b-1\}\end{aligned}
这个东西看着十分奇怪,而且前面这个方案数居然 没有让路线不碰到 y=-1 (真不是我漏了)。
好吧,我们先慢慢弄懂这个东西。
看到这样一条路径。
我把所有绿点按顺序编了个号。
那么我们该怎么计算绿点的数量呢,或者说该怎么得到答案的式子:
\begin{aligned}ans=\sum\limits_{i=0}^{a}[0,0,i,k]\times \{i,k,a,b,b-1\}\end{aligned}
我们尝试一种可行的计算方案。
首先看到绿点1、3、5、6、7、9,他们都在直线 y=k 上。
考虑对于每个这样的绿点 (i,k) 计算它在多少路线中出现:
\begin{aligned}res1=\sum\limits_{i=0}^{a}\{0,0,i,k,-1\}\times \{i,k,a,b,b-1\}\end{aligned}
就是从 (0,0) 先走到 (i,k) 再走到 (a,b),中途是不能碰到 y=-1 的。
至少式子后一项跟答案是对的上的。
然后怎么计算其他的绿点呢?
再看这样一张图。
我们把处于一段一直 y>k 的绿点分作一组。
比如上图,有 [2,3,4] 、 [8] 这两组。
那么我们可以枚举每一段的两端 (j,k) 和 (i,k)(它的两端肯定在 y=k 上,如 8 的两边 7,9 就是在 y=k 上的),在这一段中的所有点在 y=k 上面,然后统计入答案。
\begin{aligned}res2=\sum\limits_{i=0}^{a}\sum\limits_{j=0}^{i-1}\{0,0,j,k,-1\}\times \{j+1,k+1,i-1,k+1,k\}\times (i-j-1)\times \{i,k,a,b,b-1\}\end{aligned}
可以发现最后一项还是对的上的。
难不成是含 j 的那三项可以化成一个组合数?
对!
如果你觉得研究组合意义反而复杂,你可以自己尝试直接处理式子:
\begin{aligned}\sum\limits_{j=0}^{i-1}\{0,0,j,k,-1\}\times \{j+1,k+1,i-1,k+1,k\}\times (i-j-1)=<0,0,i,k,-1>\end{aligned}
其实也不难。
总之我是用了一点点组合意义再用数值代入来证的,详情让我们看到下面这个引理。
引理
定义一条合法路线以及它的权值是这样的:
-
从 (0,0) 出发,到 (a,b) 结束。
-
在行经的过程中不能碰到直线 y=-1。
-
必须与直线 y=0 在 (0,0) 外再相交至少一次。
-
设除 (0,0) 外第一处与直线 y=0 相交的点在 (i,0) ,那么这条路线的权值为 (i-1) 。
如上图就是一个合法的路线,它在 (4,0) 与 y=0 再次相交,所以这条路线的权值为 4-1=3 。
现在给你 a , b ,请你证明所有合法路线的权值和=<0,0,a,b,-1>。
证明
我们假设一条合法路线在 (i,0) 处与 y=0 再次相交。
那么可以发现答案其实就是:
\begin{aligned}ans=\sum\limits_{i=1}^{a-1}\{1,1,i-1,1,0\}\times(i-1)\times\{i,0,a,b,-1\}\end{aligned}
也就是在 (i,0) 之前与直线 y=0 没有交点,在 (i,0) 之后走到 (a,b) 且与直线 y=-1 没有交点,这样价值就是 (i-1)。
而我们思考从 (0,0) 走到 (a,b) 所有与直线 y=-1 相交的路线也可以这么计算:
\begin{aligned}<0,0,a,b,-1>=\sum\limits_{i=1}^{a-1}[0,0,i-1,-1]\times\{i,0,a,b,-1\}\end{aligned}
(其实就是考虑最后与 y=-1 的交点位置罢了)
意思就是先从 (0,0) 走到 (i-1,-1) ,再从 (i,0) 走到 (a,b) 而与 y=-1 没有交点。
然后就只要证明这个了:
\{1,1,i-1,1,0\}\times(i-1)=[0,0,i-1,-1]
这还不简单,把组合数代进去就好了。
所以 ans=<0,0,a,b,-1>。
证毕。
回到原题
我们想之前那个式子
\begin{aligned}res2=\sum\limits_{i=0}^{a}\sum\limits_{j=0}^{i-1}\{0,0,j,k,-1\}\times \{j+1,k+1,i-1,k+1,k\}\times (i-j-1)\times \{i,k,a,b,b-1\}\end{aligned}
也就是从 (0,0) 到 (j,k) 不碰 y=-1,从 (j+1,k+1) 到 (i-1,k+1) 不碰 y=k。
如图:
红色的是原题的路线。
我们可以把它变换成绿色路线的样子。
那么就是从 (i,k) 到 (0,0) 并且不碰直线 y=k+1,第一次与 y=k 相交的位置为 j 则路径价值为 (i-j-1) ,然后把原点设为 (i,k) 就都同引理了。
所以我们可以得到:
\begin{aligned}res2=\sum\limits_{i=0}^{a}<0,0,i,k,-1>\times \{i,k,a,b,b-1\}\end{aligned}
那么 \begin{aligned}res1=\sum\limits_{i=0}^{a}\{0,0,i,k,-1\}\times \{i,k,a,b,b-1\}\end{aligned}
所以 \begin{aligned}ans=res1+res2=\sum\limits_{i=0}^{a}(\{0,0,i,k,-1\}+<0,0,i,k,-1>)\times \{i,k,a,b,b-1\}\end{aligned}
得到了 \begin{aligned}ans=\sum\limits_{i=0}^{a}[0,0,i,k]\times \{i,k,a,b,b-1\}\end{aligned}。
到这里就是我的同学写出来的式子的证明了,十分神奇,不知道他怎么搞出来的
第二步:继续上面那条式子的优化。
$\begin{aligned}ans=\sum\limits_{i=0}^{a}[0,0,i,k]\times ([i,k,a,b]-<i,k,a,b,b-1>)\end{aligned}
\begin{aligned}ans=\sum\limits_{i=0}^{a}[0,0,i,k]\times ([i,k,a,b]-[i,k,a,b-2])\end{aligned}
发现这个相减的两个东西十分像,所以我们记一个新的计算 [a,b,k] :
\begin{aligned}[a,b,k] = \sum\limits_{i=0}^{a}[0,0,i,k]\times [i,k,a,b]\end{aligned}
那么 ans=[a,b,k]-[a,b-2,k]。
然后我们看到 [a,b,k] 是什么东西。
……
这不就是所有路线与直线 y=k 相交次数之和吗?
我们在 3. 中有相应的结论!
结果就是 \begin{aligned}[a,b,k]=\sum\limits_{i=\frac{a-b}{2}+k+1}^{a+1}\dbinom{a+1}{i}\end{aligned},也就是一个后缀和。
考虑到答案是两个后缀和相减。
化一下就发现,ans=\dbinom{a+1}{\frac{a-b}{2}+k+1}。
证毕。
题外话
其实在已知结论的情况下,可以直接数归,但那就失去了对组合计数方法的思考,并非本文的目的。有兴趣的读者可以自行尝试。