看完题目之后,你产生的第一个疑问一定是DLX是什么。
除非您是吊打集训队的dalao那还来看我这篇烂文干什么赶紧切题去吧
为了引入,我们先来看一道题。
已知目前有r个集合,请选出其中的一些集合使它们的并集为1,2,3,...,n,并且你要让这些选出的集合的交集为空集。
这种问题有一个名字,叫做精确覆盖问题(Exact Cover Problem)
那么我们先来想想这题该怎么做吧。
我们先用一个r行n列的矩阵来表示一个精确覆盖问题
第i行第j个元素代表第i个集合是否存在元素j
例如对于数据n=7,r=6
$S_2$ = {1,4}
$S_3$ = {4,5,7}
$S_4$ = {3,5,6}
$S_5$ = {2,3,6,7}
$S_6$ = {2,7}
它所对应一个6行7列的矩阵
```
6 7
1 0 0 1 0 0 1
1 0 0 1 0 0 0
0 0 0 1 1 0 1
0 0 1 0 1 1 0
0 1 1 0 0 1 1
0 1 0 0 0 0 1
```
我们考虑采用回溯法解决这个问题。
每一次选择一个没有被覆盖的元素,也就是一列。然后选择包含着个元素的集合进行覆盖,也就是一行。那么在矩阵中,我们每选择一个没有被删除的,接着看一下这一列中还有哪些行是1,尝试删除该行,回溯时恢复改行。当然,如果我们选了一行,那么就把这一行其它的1所在的列也应当删除。恢复同理。
这种思路又被称为算法X(Algorithm X),可惜的是删除与恢复序列并不是一个简单的操作,这个时候就应当召唤出数据结构来帮我们优化啦。那么这个数据结构支持什么呢?它应当支持删除和恢复一列。所以我们就要把目光转向著名的程序设计大师Knuth所发明的一种数据结构——舞蹈链(Dancing Links)
舞蹈链(Dancing Links)是什么?我们可以简单的将它理解为一个**双向循环交叉链表**(请大家牢记这个定义)
使用舞蹈链的算法X又被称为DLX
(不会链表的同学可以自行百度哦)
把上面那句话对应到程序中是怎么样的呢,首先处理**双向**
对于每一个节点,我们都给它两个指针L与R。分别表示这个节点的左边节点编号和右边节点编号。
接着处理**交叉**
什么叫交叉?横纵即为交叉。横的链表我们已经设计了。那么考虑下纵链表,再给每个节点两个指针U与D。分别表示这个节点上方节点编号与下方节点编号。
最后处理**循环**
我们让最右边的所有节点的R指向最左边的节点,最左边节点的L指向最右边的节点,上下也是如此。
那矩阵如何对应到舞蹈链里呢?
_我们把矩阵的每一个1节点对应到舞蹈链的一个节点_
那么问题来了,如何删除一列呢?
我们可以在每个纵链表的顶端添加一个节点——**虚拟节点**
该节点的U指向其所在列的最后一个节点,D指向其所在列的第一个节点。L与R分别指向旁边两列的虚拟节点。
那么删除一列只需要将该列虚拟节点左边的节点的R指向该列虚拟节点右边的虚拟节点,将该列所对虚拟节点的右边虚拟节点的L指向该列所对虚拟节点的左边的虚拟节点。(好好理解下)
问题是删完了吗?没有,这一列里还有节点跟其他节点连着呢。
所以我们应当将该列所有节点找到,然后再把这列所有节点所在的所有行的其它节点的上下节点互指。这样就删完一列了。
那么恢复一列不就是逆操作嘛?
所以一个Dancing Links大概就是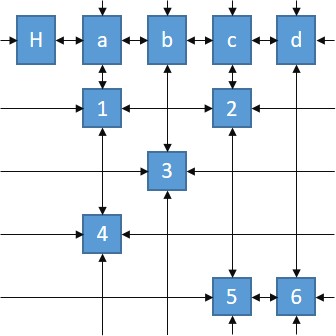这样的。
什么?有点晕?不如上上代码看看?不懂的地方可以看一下注释哦。
```cpp
//顺着链表a,遍历除s以外的所有元素
#define FOR(i,a,s) for(int i = a[s]; i != s ; i = a[i])
struct DLX
{
int n,sz;
int head;
int l[maxnode],r[maxnode],u[maxnode],d[maxnode];
int s[MAXN];//s[i]代表第i列节点的个数
int col[maxnode],row[maxnode];
//row[i] 代表节点i在第几行,col[i]代表节点i在第几列
int ans[MAXN];//答案栈
int ansd;
void init()
{
head = 0;
for(int i=0;i<=m;i++)//有m列,处理m个虚拟节点
//从0开始是因为还有一个head节点
{
u[i] = i;
d[i] = i;
l[i] = i - 1;
r[i] = i + 1;
//这里没必要维护row与col因为维护了也没卵用
}
r[m] = head;
l[head] = m;
//链表循环
sz = m + 1;
memset(s,0,sizeof(s));
}
void addRow(int R,vector <int> columns)//添加第r行,cloumns[i]代表第r行存在哪些数
//例如colums = {1,2,9},代表01矩阵中第r行第2个是1,如此类推
{
int first = sz;
for(int i=0;i<columns.size();i++)
{
int c = columns[i];
//维护当前节点
l[sz] = sz - 1;
r[sz] = sz + 1;
//当前节点的左边是上一节点,右边是下一节点
d[sz] = c;
u[sz] = u[c];
//由于c是当前列的编号,也就是该列虚拟节点的编号,那么u[c]其实是目前节点上方的节点编号
//为了使链表循环,每一个链表的最后一个节点的下方应当指向head节点,head节点的上方应当指向下方节点
d[u[c]] = sz;
//上一个节点的下方此时不应当是head了而应当是当前节点
u[c] = sz;
//重新使链表循环
col[sz] = c;
row[sz] = R;
//维护col和row
++s[c];
++sz;
}
r[sz-1] = first ;l[first] = sz - 1;
//使链表循环
}
void remove(int c)//删除第c列
{
r[l[c]] = r[c];
l[r[c]] = l[c];
//先删虚拟节点
FOR(i,d,c)//遍历第c列的down列表
FOR(j,r,i)//遍历第c列每个节点
{d[u[j]] = d[j] , u[d[j]] = u[j] , --s[col[j]] ;}//删除上述遍历的所有节点
}
void restore(int c)//恢复 = 删除逆操作,不解释
{
FOR(i,u,c)
FOR(j,l,i)
{++s[col[j]] , d[u[j]] = j,u[d[j]] = j;}
r[l[c]] = c;
l[r[c]] = c;
}
//前方高能!!!!!!!!! 该算法最美丽的地方!
bool dance(int step)//step为递归深度
{
if(r[head] == head)//找到解
{
ansd = step;
return true;
}
int c = r[head];//第一个没被删除的列
FOR(i,r,head)
if(s[i] < s[c])
c = i;
//贪心找节点最少的一列,这样可以让枚举情况最少
remove(c);//删除
FOR(i,d,c)//c列表下的每一个节点
{
//目前选取第row[i]行来覆盖
//那么就应当把第row[i]行所覆盖的其他列也给删除
ans[step] = row[i];
FOR(j,r,i)
remove(col[j]);
if(dance(step + 1))
return true;//如果找到解了,直接返回
//要不然还要恢复并且尝试下一个i
FOR(j,l,i)
restore(col[j]);
}
restore(c);
//恢复
return false;
}
void print()//输出解
{
for(int i = 0;i<ansd;i++)
cout<<ans[i]<<' ';
}
};
```
有没有看到一个舞者在你的链表上跳舞呢?主部分又被称作dance。
你认为舞蹈链就这么点用处?那可就大错特错了!
你听说过八皇后问题吗?你听说过数独问题吗?
没错DLX算法还是一种用来处理数独的方法!
它是目前跑的最快的处理数独的算法!
怎么用它来处理数独呢?那么我们就要把数独问题转换成精确覆盖问题了。
这也谈到了一个精确覆盖问题的建模。不过也非常简单,每列代表一个限制条件,每行代表一种方案,若方案i满足限制j,则矩阵mat[i][j]=1,因此矩阵的构造既要满足所有限制条件,又不能漏掉可能的方案。
对于数独,我们先看限制
```
每行中每个数只能出现一遍,ROW(x,v)表示第x行有数字v。
每列中每个数只能出现一遍,COL(x,v)表示第x列有数字v。
每宫中每个数只能出现一遍,BLOCK(i,v)表示编号为i的九宫格块内有数字v
每格中只能填一个数,EXIST(x,y)表示第x行y列有数字。
```
那么应当会有324行
再看决策,定义三元组(r,c,v)代表第r行第c个填v
那么决策(r,c,v)所能满足的限制就是
```
ROW(r,v)
COL(c,v)
BLOCK(zu(r,c),v)
EXIST(r,c,v)
```
(其中zu(r,c)代表点(r,c)所在的九宫格的编号)
列应当有729列。
那么这样,我们不就把数独转换成了精确覆盖问题了嘛?
------------
2018.10.19更新:我发现LG多了一个DLX模板,泥萌可以做做
~~虽然已经没有人看我这篇烂东西了~~
作业:LG P1074 P1784
然后自己找题去吧(逃)
------------
参考文献:
[1] 刘汝佳 《算法竞赛入门经典训练指南》
[2] 图片出处 :hihocoder