推荐在 cnblogs 阅读。
1. 复数和单位根
前置知识:弧度制,三角函数。
1.1 复数的引入
跳出实数域 \mathbb R,我们定义 i ^ 2 = -1,即 i = \sqrt {-1},并在此基础上定义 复数 a + bi,其中将 b\neq 0 的称为 虚数。复数域记为 \mathbb C。
像这种从 a 变成 a + bx 的 扩域 操作并不少见,例如初中学习 “平方根” 时,经常用 a + b\sqrt x(x > 0) 表示一个数。这类数的加减乘都是容易的,除法即考虑平方差公式 (c + d\sqrt x)(c - d\sqrt x) = c ^ 2 - d ^ 2x,因此 \frac {a + b\sqrt x} {c + d\sqrt x} = \frac {(ac - bdx) + (bc - ad)\sqrt x} {c ^ 2 - d ^ 2 x}。
将 x 替换为 -1,复数四则运算可由实数四则运算结合 i 的定义直接推广得到。
- 加法:(a + bi) + (c + di) = (a + c) + (b + d)i。
- 减法:(a + bi) - (c + di) = (a - c) + (b - d)i。
- 乘法:(a + bi)(c + di) = (ac - bd) + (ad + bc)i。
- 除法:\frac {a + bi} {c + di} = \frac {(a + bi)(c - di)} {(c + di)(c - di)} = \frac {ac + bd} {c ^ 2 + d ^ 2} + \frac {bc - ad} {c ^ 2 + d ^ 2} i。
1.2 复平面与棣莫弗定理
描述一个复数 a + bi 需要两个值 a 和 b,其中 a 表示 实部,b 表示 虚部。这启发我们将其放在平面直角坐标系上描述,称为 复平面。其在复平面上的坐标为 (a, b),实部 a 为横坐标,虚部 b 为纵坐标。
一个复数唯一对应一个平面向量,因为它们都可以用有序实数对描述。将向量起点平移至原点,则其终点指向与其对应的复数。考虑平面向量的一些特征,如其长度与所在直线斜率。将这些概念应用在复数上,我们得到如下定义:
- 定义复数 z = a + bi 的 模 为 |z| = \sqrt {a ^ 2 + b ^ 2}。
- 定义复数 z = a + bi 的 辐角 为 \operatorname{Arg} z = \theta,其中 \tan \theta = \frac b a。满足 -\pi < \theta \leq \pi 的 \theta 称为 辐角主值,记作 \operatorname{arg} z,即 \operatorname{arg} z = \arctan \frac b a。
- 辐角确定了 z 所在直线,模确定了 z 在直线上的长度。对比实部和虚部,模和辐角主值以另一种有序实数对的形式描述复数。
根据 z = a + bi 的模 r 和辐角 \theta,可知 z 的实部 a = r\cos \theta,虚部 b = r \sin \theta,据此定义复数的 三角形式 z = r(\cos \theta + i\sin \theta)。
利用 \cos 和 \sin 的和角公式可得 z_1z_2 = r_1r_2(\cos(\theta_1 + \theta_2) + i\sin (\theta_1 + \theta_2))。该等式称为 棣莫弗定理,它说明 复数相乘,模长相乘,辐角相加。
- 根据棣莫弗定理,我们得到对虚数单位 i 的一种直观理解:将一个复数 z 乘以 i 相当于将其 逆时针旋转 \frac {\pi} 2 弧度。实际上,考虑虚数单位 i 本身在复平面上的位置,发现就是 1 逆时针旋转 \frac {\pi} 2 度。一般地,有旋转的地方就有 i 存在,i 即旋转。推荐观看:虚数的来源 - Veritasium。
1.3 单位根的定义
当 r = 1 时,z = \cos\theta + i\sin\theta 在单位圆上。此时根据棣莫弗公式有 z ^ n = \cos(n\theta) + \sin(n\theta),它在 复数旋转 和 复数乘法 之间构建了桥梁:z 的 n 次幂相当于从 (1, 0) 开始,以 z 的角度在单位圆上旋转 n 次得到的结果,称为将 z 旋转 n 次。
考虑将单位圆 n 等分(如下图),取任意 n 等分点 P_k(0\leq k < n),将其旋转 n 次均得到 1,因为跨过的 \frac 1 n 单位圆弧数为 n 的倍数。这说明 P_k ^ n = 1。
探究 P_k 的表达式:因为它相当于从 1 开始在单位圆上旋转 \frac {2k\pi} n 弧度,因此 P_k = \cos\left(\frac {2k\pi} n\right) + \sin\left(\frac {2k\pi} n\right)。我们称所有 P_k 为 n 次 单位根,将 P_1 记作 \omega_n,则 P_k = P_1 ^ k = \omega_n ^ k。
根据 P_k ^ n = 1 可知任意 n 次单位根 \omega_n ^ k 均为 x ^ n - 1 = 0 的解。除特殊说明外,一般 n 次单位根直接代指 \omega_n,即从 1 开始逆时针方向的第一个单位根。
可以观看 3b1b 的视频 从 6:00 到 7:30 的部分加深对上述内容的理解。
- 单位根的循环性:由 \omega_n ^ n = 1 单位根的指数可对 n 取模。换言之,考虑从 1 开始不断乘以 \omega_n,我们将得到 1, \omega_n, \omega_n ^ 2, \cdots, \omega_{n} ^ {n - 1}, \omega_n ^ n = 1, \omega_n ^ {n + 1} = \omega_n, \cdots,循环节为 n。想象从 1 开始不断旋转 \frac {2\pi} n 弧度,旋转 n 次后我们将落入循环。换言之,\omega_n ^ k = \omega_n ^ {k + tn}(t\in \mathbb Z)。
-
- 当 n 为偶数时,将 \omega ^ k_n 取反相当于将其逆时针(或顺时针)转半圈,所以 -\omega_n ^ k = \omega_n ^ {k\pm \frac n 2}(2\mid n)。
- 单位根的对称性:因为 n 次单位根将单位圆 n 等分,均匀分布在圆周,所以它们的重心就在原点,即 \sum_{i = 0} ^ {n - 1} \omega_{n} ^ i = 0。
- 若 \gcd(k, n) = 1,则 \omega_n ^ k 称为 本原单位根。所有本原单位根的 0\sim n - 1 次幂互不相同。
1.4 单位根与原根
前置知识:原根,详见 初等数论学习笔记 I:同余相关。
单位根和原根有极大的相似性,可以说原根就是模 P 下的整数域的单位根。
设 n = \varphi(P) 且 P 存在原根 g,则 g ^ 0, g ^ 1, \cdots, g ^ {n - 1}, g ^ n = g ^ 0, g ^ {n + 1} = g ^ 1 这样的循环和 n 次单位根的循环一模一样。这使得在模 P 意义下涉及 n 次单位根运算时,可直接用原根 g 代替。进一步地,对于 d\mid n,g ^ {\frac n d} 可直接代替模 P 意义下的 d 次单位根。
- 单位根和原根都是对应域上一个大小为 n = \varphi(P) 的 循环群 的 生成元。它们均满足 n 次幂是对应域的单位元,且它们的 0\sim n - 1 次幂互不相同。换言之,它们 同构。
快速傅里叶变换 FFT 和快速数论变换 NTT 的联系恰在于此。
1.5 欧拉公式
前置知识:自然对数 \ln 的底数 e 及其相关性质。
这部分为接下来可能用到的符号做一些补充。
欧拉公式指出
e ^ {ix} = \cos x + i\sin x
即单位圆上从 (1, 0) 开始旋转 x 弧度得到的复数,也即大小为 x 的角的终边与单位圆的交点。
欧拉公式的严谨证明超出了讨论范围,相关资料可以参考百度百科。我们给出一个对欧拉公式的感性理解方式,以加深读者对欧拉公式的直观印象与理解,来自 在 3.14 分钟内理解 e ^ {i\pi} - 3Blue1Brown。这个视频相当有启发性。
根据 (e ^ t)' = e ^ t,考虑 e ^ t 随着 t 增大在数轴上的取值。e ^ t 以每秒钟 t 均匀增加 1 的速度向数轴正方向移动,则 e ^ t 的速度就是它本身的位置。它的起始点为 e ^ 0 = 1。
根据 (e ^ {kt})' = ke ^ t,类似可知 e ^ {kt} 的速度等于 k 倍它本身的位置。
当 k = i 时,速度相当于将本身的位置逆时针旋转 \frac {\pi} 2 弧度,与位置垂直。这样,根据基础的高中物理知识,我们知道 e ^ {it} 随着 t 增大,在单位圆上做匀速圆周运动,且每秒移动 1 弧度。
这样,e ^ {it} 就等于模长为 1,辐角为 t 的复数,即 \cos t + i\sin t。这使得我们可以用 r e ^ {i\theta} 描述模长为 r,辐角为 \theta 的复数,记号变得更简洁。
将该表示法应用至单位根,可知 \omega_n = e ^ {\frac {2\pi i} n}。
读者应当在 re ^ {i\theta},r(\cos\theta + i\sin \theta) 及其在复平面上的位置建立直观联系,有助于理解接下来的内容。
带入 t = \pi,得到著名等式
e ^ {i\pi} = -1
带入 t = 2\pi = \tau,得
e ^ {i\tau} = 1
这说明对于任意 k\in \mathbb Z,(e ^ {2\pi i}) ^ {k + \frac t n} 相等恰对应 \omega_n ^ {kn + t} 相等。
2. 多项式
2.1 基本概念
形如 \sum_{i = 0} ^ n a_ix ^ i 的 有限和式 称为 多项式,记作 f(x) = \sum_{i = 0} ^ n a_i x ^ i。其中,a_i 称为 i 次项的 系数,也称 x ^ i 前的系数,记作 [x ^ i]f(x)。超出最高次数 n 的系数 a_i(i > n) 视作 0。
当项数无限时,和式形如 \sum_{i = 0} ^ {\infty} a_ix ^ i,称为 形式幂级数,它暂时超出了我们的讨论范围。
- 多项式 系数非零 的最高次项的次数称为该多项式的 度,也称次数,记作 \deg f。如 f(x) = \sum_{i = 0} ^ n a_i x ^ i 其中 a_n \neq 0,则 f 为 n 次多项式,记作 \deg f = n。
- 使得 f(x) = 0 的所有 x 称为多项式的 根。
- 若 a_i 均为实数,则称 f 为实系数多项式。若 a_i 可以均为复数,则称 f 为复系数多项式。
- 代数基本定理:任何非零一元 n 次复系数多项式恰有 n 个复数根。这些复数根可能重合。证明略。
2.2 系数表示法和点值表示法
将 $x = x_i$ 带入,得到 $y_i = f(x_i)$,称 $(x_i, y_i)$ 为 $f$ 在 $x_i$ 处的点值。用若干点值 $(x_i, y_i)$ 描述多项式的方法称为 **点值表示法**。
考虑这两种表示法之间的联系。我们尝试探究在给定 $n$ 个点值 $(x_0, y_0), (x_1, y_1), \cdots, (x_{n - 1}, y_{n - 1})$ 其中 $x_i$ 互不相同时,所唯一确定的多项式的最高次数。
一个自然的猜测是 $n - 1$,因为 $n - 1$ 次多项式需要 $n$ 个系数描述,具有 $n$ 单位信息,而 $n$ 个点值同样具有 $n$ 单位信息。
证明即考虑直接带入,得到 $n$ 元线性方程组:对于任意 $0\leq j < n$,$\sum_{i = 0} ^ {n - 1} a_ix_j ^ i = y_j$。该线性方程组的系数矩阵为
$$
\begin{bmatrix}
1 & x_0 & x_0 ^ 1 & \cdots & x_0 ^ {n - 1} \\
1 & x_1 & x_1 ^ 1 & \cdots & x_1 ^ {n - 1} \\
1 & x_2 & x_2 ^ 1 & \cdots & x_2 ^ {n - 1} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
1 & x_{n - 1} & x_{n - 1} ^ 2 & \cdots & x_{n - 1} ^ {n - 1} \\
\end{bmatrix}
$$
因 $x_i$ 互不相同,所以该范德蒙德矩阵的行列式非零,方程组有唯一解。类似的,从线性方程组的角度出发,容易证明 $n$ 个点值不可能唯一确定 $n$ 次或更高次的多项式。
综上,我们得到重要结论:**$n$ 个点值唯一确定的多项式最高次数为 $n - 1$**。
- 从系数表示法转为点值表示法称为 **求值**(Evaluation)。
- 从点值表示法转为系数表示法称为 **插值**(Interpolation)。
### 2.3 多项式运算
#### 2.3.1 基本运算
设 $f(x) = \sum_{i = 0} ^ n a_i x ^ i$,$g(x) = \sum_{i = 0} ^ m b_i x ^ i$。
- 设 $h = f + g$,则 $h(x) = (\sum_{i = 0} ^ n a_i x ^ i) + (\sum_{j = 0} ^ m b_j x ^ j) = \sum_{i = 0} ^ {\max(n, m)} (a_i + b_i) x ^ i$,可知两多项式相加,对应系数相加,$\deg (f + g) = \max(\deg f, \deg g)$。
- 设 $h = f * g$,则 $h(x) = (\sum_{i = 0} ^ n a_i x ^ i)(\sum_{j = 0} ^ m b_j x ^ j) = \sum_{i = 0} ^ {n + m} (\sum_{j = 0} ^ i a_jb_{i - j}) x ^ i$,可知两多项式相乘,每两个系数相乘贡献至次数之和的系数,$\deg(f * g) = \deg f + \deg g$。
因此,在系数表示法下,计算两个多项式相加的复杂度为 $\mathcal{O}(n + m)$,计算两个多项式相乘的复杂度为 $\mathcal{O}(nm)$。
- 根据 $(f + g)(x) = f(x) + g(x)$,可知两个多项式相加时,对应点值相加。
- 根据 $(fg)(x) = f(x) g(x)$,可知两个多项式相乘时,对应点值相乘。
因此,在点值表示法下,计算两个多项式相加需要 $\max(n, m) + 1$ 个点值,计算两个多项式相乘需要 $n + m + 1$ 个点值,复杂度均为 $\mathcal{O}(n + m)$。
- 用 $f * g$ 和 $fg$ 表示多项式相乘,即进行加法卷积;用 $f \cdot g$ 表示多项式 **点乘**,即 **对应系数相乘**。
在系数表示法下计算两个多项式相乘,我们首先将其转化为点值表示法,相乘后再转回系数表示法。时间复杂度 $\mathcal{O}((n + m)\log (n + m))$。相关算法将在第四章介绍。
## 3. 拉格朗日插值
在 2.2 小节我们得到结论:$n$ 个点值唯一确定的多项式最高次数为 $n - 1$。那么,如何在点值表示法和系数表示法之间快速转换呢?
从系数表示法转为点值表示法,最常用的方法是直接带入,时间复杂度 $\mathcal{O}(n ^ 2)$。$\mathcal{O}(n\log ^ 2 n)$ 的多项式多点求值则需要高级多项式技巧,此处不作介绍。
从点值表示法转为系数表示法,最直接的方法是高斯消元,时间复杂度 $\mathcal{O}(n ^ 3)$。接下来我们将介绍常用的拉格朗日插值法。
### 3.1 算法详解
拉格朗日插值的核心思想在于利用点值的可加性,**每次只考虑一个点值**,其它点值均视为 $0$,由此构造 $n$ 个多项式 $f_i(x)$,使得它们在 $x_i$ 处取值为 $y_i$,$x_j(j\neq i)$ 处取值为 $0$,则 $f = \sum_{i = 0} ^ {n - 1} f_i$。**中国剩余定理** 使用了类似的思想。
为了让 $f_i(x_j) = 0\ (i\neq j)$,$f_i$ 应包含 $x - x_j$ 作为因式,因此设 $f_i(x) = \prod_{i \ne j} (x - x_j)$。但是此时 $f_i(x_i)$ 不一定等于 $y_i$,我们发现可以调整 $f_i$ 的系数,给 $f_i$ 乘上 $\frac {y_i} {f_i(x_i)}$。综上,我们得到 $f_i$ 的表达式
$$
f_i(x) = y_i \prod_{j \neq i} \frac {x - x_j} {x_i - x_j}
$$
对 $f_i$ 求和得 $f$,我们得到拉格朗日插值公式
$$
f(x) = \sum\limits_{i = 0} ^ {n - 1} y_i \prod\limits_{j \neq i} \frac {x - x_j} {x_i - x_j}
$$
为得到 $f$ 的各项系数,只需 $\mathcal{O}(n ^ 2)$ 求出 $F(x) = \prod_{i = 0} ^ {n - 1} (x - x_i)$,对每个 $i$ 暴力 $\mathcal{O}(n)$ 将 $F$ 除掉一次式 $x - x_i$ 算出 $\frac {F(x)} {x - x_i}$ 的各项系数,再乘以 $\frac {y_i} {\prod_{j \neq i} x_i - x_j}$ 得到 $f_i$,则 $f = \sum_{i = 0} ^ {n - 1} f_i$。时间复杂度 $\mathcal{O}(n ^ 2)$。
通常情况下,题目要求我们求出 $F(x)$ 在给定某个 $x$ 处的取值,此时我们不把 $x$ 看做函数的元,而是直接将 $x$ 带入上式。时间复杂度仍为 $\mathcal{O}(n ^ 2)$。
多项式快速插值在 $\mathcal{O}(n\log ^ 2 n)$ 的时间内将点值表示法转化为系数表示法,这超出了我们的讨论范围。
### 3.2 连续取值插值
当给定点值横坐标为连续整数时,我们有快速单点插值的方法。
以 $0, 1, \cdots, n - 1$ 即 $x_i = i$ 为例:
$$
\begin{aligned}
f(x) = \sum\limits_{i = 0} ^ {n - 1} y_i \prod\limits_{j \neq i} \frac {x - j} {i - j} \\
\end{aligned}
$$
分子是 $\prod (x - i)$ 挖掉一个项,经典维护前缀后缀积。设 $p_i = \prod_{j = 0} ^ {i - 1} x - j$,$s_i = \prod_{j = i + 1} ^ {n - 1} x - j$。
分母对于 $i > j$,$\prod_{j = 0} ^ {i - 1} (i - j) = i!$。对于 $i < j$,$\prod_{j = i + 1} ^ {n - 1} (i - j) = (-1)(-2) \cdots (i - n + 1)$,将所有负号提出来,得 $(-1) ^ {n - i + 1}(i - n + 1)!$。
因此
$$
f(x) = \sum\limits_{i = 0} ^ {n - 1} y_i \frac {p_is_i} {(-1) ^ {n - i + 1} i! (i - n + 1)!}
$$
预处理阶乘逆元,时间复杂度 $\mathcal{O}(n)$。
### 3.3 应用
- 计算范德蒙德方阵的逆矩阵,详见 4.4.1 小节。
### 3.4 例题
#### [P4781 【模板】拉格朗日插值](https://www.luogu.com.cn/problem/P4781)
```cpp
#include <bits/stdc++.h>
using namespace std;
constexpr int N = 2e3 + 5;
constexpr int mod = 998244353;
int ksm(int a, int b) {
int s = 1;
while(b) {
if(b & 1) s = 1ll * s * a % mod;
a = 1ll * a * a % mod, b >>= 1;
}
return s;
}
int n, k, ans, x[N], y[N];
int main() {
cin >> n >> k;
for(int i = 1; i <= n; i++) cin >> x[i] >> y[i];
for(int i = 1; i <= n; i++) {
int deno = 1, nume = 1;
for(int j = 1; j <= n; j++) {
if(i == j) continue;
deno = 1ll * deno * (x[i] + mod - x[j]) % mod;
nume = 1ll * nume * (k + mod - x[j]) % mod;
}
ans = (ans + 1ll * y[i] * nume % mod * ksm(deno, mod - 2)) % mod;
}
cout << ans << "\n";
return 0;
}
```
## 4. 快速傅里叶变换
快速傅里叶变换(Fast Fourier Transform,FFT)是多项式算法的根基。想要真正理解它,必须先真正理解单位根,还需要对线性代数有基本了解。
推荐观看:
- [这个算法改变了世界 - Veritasium](https://www.bilibili.com/video/BV1CY411R7bA/)。
- [The Fast Fourier Transform (FFT): Most Ingenious Algorithm Ever? - Reducible](https://www.youtube.com/watch?v=h7apO7q16V0) & [B 站搬运](https://www.bilibili.com/video/BV1za411F76U/)。
### 4.1 求值的本质
设 $f(x) = \sum_{i = 0} ^ {n - 1} a_i x ^ i$,将 $x_0$ 带入,得 $f(x_0) = \sum_{i = 0} ^ {n - 1} a_i x_0 ^ i$。考虑将其写成向量内积(点积)的形式:
$$
f(x_0) = \sum_{i = 0} ^ {n - 1} a_i x_0 ^ i =
\begin{bmatrix}
x_0 ^ 0 & x_0 ^ 1 & \cdots & x_0 ^ {n - 1}
\end{bmatrix}
\times
\begin{bmatrix}
a_0 \\ a_1 \\ \vdots \\ a_{n - 1}
\end{bmatrix}
$$
这样,如果有 $x_0, x_1, \cdots, x_{m - 1}$ 需要求值,整个过程就可以写成 $m\times n$ 维矩阵乘以 $n$ 维列向量的形式:
$$
\begin{bmatrix}
x_0 ^ 0 & x_0 ^ 1 & \cdots & x_0 ^ {n - 1} \\
x_1 ^ 0 & x_1 ^ 1 & \cdots & x_1 ^ {n - 1} \\
\vdots & \vdots & \ddots & \vdots \\
x_{m - 1} ^ 0 & x_{m - 1} ^ 1 & \cdots & x_{m - 1} ^ {n - 1} \\
\end{bmatrix}
\times
\begin{bmatrix}
a_0 \\ a_1 \\ \vdots \\ a_{n - 1}
\end{bmatrix}
=
\begin{bmatrix}
f(x_0) \\ f(x_1) \\ \vdots \\ f(x_{m - 1})
\end{bmatrix}
$$
左侧矩阵就是著名的 **范德蒙德矩阵**。
当 $m = n$ 时为范德蒙德方阵,$x_i$ 互不相同时其逆存在,帮助我们快速从点值表示法转回系数表示法。$m > n$ 时任取 $x_i$ 互不相同的 $n + 1$ 行可以求逆。$m < n$ 时无法还原系数。这体现出 $n + 1$ 个点值唯一确定最高次数不超过 $n$ 的多项式。
朴素计算求值的复杂度为 $\mathcal{O}(nm)$,因为带入求值一次的复杂度为 $\mathcal{O}(n)$。快速傅里叶变换即在离散傅里叶变换基础上通过选取合适的 $x_i$,使得可以快速求值。
### 4.2 离散傅里叶变换
在介绍 FFT 之前,我们先给出离散傅里叶变换(Discrete Fourier Transform,DFT)的概念。
DFT 在工程中是将离散信号从时域转为频域的过程。碰巧的是,其表达式刚好可以用来对多项式进行多点求值,只不过这些点值是固定的 **单位根** 处的点值,但对于求值做多项式乘法已经足够了。
DFT 将一个长度为 $N$ 的复数序列 $x_0, x_1, \cdots, x_{N - 1}$ 通过如下公式转化为另一个长为 $N$ 的复数序列 $X_0, X_1, \cdots, X_{N - 1}$:
$$
X_k = \sum_{n = 0} ^ {N - 1} x_n e ^ {-\frac {2\pi i} Nkn}
$$
也即
$$
X_k = \sum_{n = 0} ^ {N - 1} x_n \omega_N ^ {-kn}
$$
设多项式 $f(x) = \sum_{n = 0} ^ {N - 1} x_n x ^ i$,易知
$$
X_k = \sum_{n = 0} ^ {N - 1} x_n(\omega_N ^ {-k}) ^ n = f(\omega_N ^ {-k})
$$
根据上式,离散傅里叶变换可以看成多项式 $f(x) = \sum_{n = 0} ^ {N - 1} x_nx ^ i$ 在 $N$ 个单位根处求值。
没看懂?没关系。接下来我们将从另一角度出发,得到一个差别微小但更容易理解的算法 —— FFT。
### 4.3 算法详解
首先我们得搞清楚,DFT 是一个变换,而 FFT 是用于实现 DFT 的算法。在 FFT 的推导过程中,其所实现的变换和 DFT 变换有细微的差别,因此笔者也用 FFT 表示该算法实现的变换。
按理说学习一个算法时需要搞清楚它的用途,但如果直接从 DFT 角度入手尝试简化流程,那么为了让动机看起来自然,我们还要先学习 DFT 的实际含义,这涉及到大量前置知识。
但是,从计算机科学界尤为重要且为各位 OIer 熟知的多项式乘法的优化出发,我们通过自然推理得到一个算法,而该算法恰好可以快速实现 DFT(有一些细小的差别,详见 4.3.5)。
我们明确接下来的目标:给定次数 $n - 1$ 的多项式 $f(x) = \sum_{i = 0} ^ {n - 1} a_i x ^ i(a_{n - 1} \neq 0)$,快速求出它的至少 $n$ 个点值。
下文中,$f(x)$ 也被视为关于 $x$ 的 $n - 1$ 次函数。
#### 4.3.1 简化情况
解决一个普遍性的问题,最重要的思想就是 **从简化情况入手,分析问题的性质**。
函数的性质无非就那几个:奇偶性,单调性,周期性等。一般函数没有单调性和周期性,但总可以表示为一个偶函数和一个奇函数之和,这一定是突破点。
- 对于偶函数 $f(x)$,即所有奇数次项系数为 $0$,带入两个相反数 $w$ 和 $-w$ 时,它们的值相等。
- 对于奇函数 $f(x)$,即所有偶数次项系数为 $0$,带入两个相反数 $w$ 和 $-w$ 时,它们的值互为相反数。
因此,将任意多项式 $f(x)$ 拆成偶函数 $f_e(x)$ 和奇函数 $f_o(x)$ 之和,则
$$
\begin{cases}
f(x) = f_e(x) + f_o(x) \\
f(-x) = f_e(x) - f_o(x)
\end{cases}
$$
选择 $\lceil\frac n 2\rceil$ 对两两互为相反数的值 $(x_i, -x_i)$ ,求出所有 $x_i$ 在 $f_e(x)$ 和 $f_o(x)$ 处的取值。
不妨设 $n$ 为偶数,则 $f_e$ 是 $n - 2$ 次多项式,$f_e$ 是 $n - 1$ 次多项式,本质上依然相当于求出 $n - 1$ 次多项式的 $n$ 个点值,对时间复杂度没有优化。
但是 $f_e$ 和 $f_o$ 的项数减半,尝试利用该性质。
因为 $f_e$ 只有偶数次项 $a_0x ^ 0 + a_2x ^ 2 + \cdots$,故考虑换元 $u = x ^ 2$,则 $f_e(u) = a_0u ^ 0 + a_2 u ^ 1 + \cdots$。换言之,我们设 $f'_e(x) = a_0x ^ 0 + a_2x ^ 1 + \cdots$,则 $f_e(x) = f'_e(x ^ 2)$。
同理,从 $f_o$ 中提出一个 $x$,设 $f'_o(x) = a_1x ^ 0 + a_3x ^ 1 + \cdots$,则 $f_o(x) = xf'_o(x ^ 2)$。
因此,
$$
\begin{cases}
f(x) = f'_e(x ^ 2) + xf'_o(x ^ 2) \\
f(-x) = f'_e(x ^ 2) - xf'_o(x ^ 2)
\end{cases}
$$
这样才是真正意义上的规模减半。若问题可递归,则时间复杂度为 $T(n) = 2T\left(\frac n 2\right) + \mathcal{O}(n)$,解得 $T(n) = \mathcal{O}(n\log n)$。
#### 4.3.2 引入单位根
问题来了,如何保证递归得到的问题也满足两两互为相反数呢?
考虑一开始的 $(x_i, -x_i)$,这说明存在 $i'$ 使得 $x_i ^ 2 = -x_{i'} ^ 2$,它们互不相同但它们的 $4$ 次方相等。
进一步推演,因为问题会递归 $w = \lceil\log_2 n\rceil$ 层,所以我们需要找到 $k = 2 ^ w$ 个互不相等的 $x$,但它们的 $k$ 次幂相等。这个相等的 $k$ 次幂可以任意选择,方便起见设为 $1$,则 $x ^ k = 1$,$x$ 为所有 $k$ 次单位根。
逆推得到结果后,我们再顺着检查一遍:初始令 $x$ 为所有 $k$ 次单位根,每层递归会将这些数平方,得到所有 $\frac k 2, \frac k 4 \cdots$ 次单位根。因为 $\frac k 2, \frac k 4, \cdots$ 都是偶数,所以它们可以两两正负配对,直到递归 $w$ 层的平凡情况:$\frac k {2 ^ w} = 1$ 次单位根即 $x = 1$。
由此可得通常使用(补齐到 $2$ 的幂)的快速傅里叶变换的范德蒙德方阵形式:
$$
\begin{bmatrix}
(\omega_n ^ 0) ^ 0 & (\omega_n ^ 0) ^ 1 & \cdots & (\omega_n ^ 0) ^ {n - 1} \\
(\omega_n ^ 1) ^ 0 & (\omega_n ^ 1) ^ 1 & \cdots & (\omega_n ^ 1) ^ {n - 1} \\
\vdots & \vdots & \ddots & \vdots \\
(\omega_n ^ {n - 1}) ^ 0 & (\omega_n ^ {n - 1}) ^ 1 & \cdots & (\omega_n ^ {n - 1}) ^ {n - 1} \\
\end{bmatrix}
\times
\begin{bmatrix}
a_0 \\ a_1 \\ \vdots \\ a_{n - 1}
\end{bmatrix}
=
\begin{bmatrix}
f(\omega_n ^ 0) \\ f(\omega_n ^ 1) \\ \vdots \\ f(\omega_n ^ {n - 1})
\end{bmatrix}
$$
#### 4.3.3 递归公式
得到大致框架后,我们具体地描述整个算法流程:
首先将 $n$ 补齐到不小于 $n$ 的最小的 $2$ 的幂,即 $2 ^ {\lceil \log_2 n\rceil}$。
设当前需要求值的多项式 $f$ 长度为 $L(L = 2 ^ w, w\in \mathbb N)$,若 $L = 1$ 则直接返回 $a_0$。否则我们需求出 $f(x)$ 在所有 $L$ 次单位根 $\omega_L ^ k(0\leq k < L)$ 处的取值。
将 $f(x)$ 写成 $f_e(x ^ 2) + xf_o(x ^ 2)$,则对于 $0\leq k < \frac L 2$,有
$$
\begin{aligned}
f(\omega_L ^ k) & = f_e(\omega_L ^ {2k}) + \omega_L ^ k f_o(\omega_L ^ {2k}) \\
f(\omega_L ^ {k + \frac L 2}) & = f_e(\omega_L ^ {2k + L}) + \omega_L ^ {k + \frac L 2} f_o(\omega_L ^ {2k + L})
\end{aligned}
$$
根据单位根的性质(在单位根部分有介绍):
- $\omega_n ^ k = \omega_{2n} ^ {2k}$。
- $\omega_n ^ k = \omega_n ^ {k + tn}(t\in \mathbb Z)$。
- $\omega_{n} ^ k = -\omega_{n} ^ {k + \frac n 2} (2\mid n)$。
得
$$
\begin{aligned}
f(\omega_L ^ k) & = f_e(\omega_{\frac L2} ^ {k}) + \omega_L ^ k f_o(\omega_{\frac L 2} ^ {k}) \\
f(\omega_L ^ {k + \frac L 2}) & = f_e(\omega_{\frac L2} ^ {k}) - \omega_L ^ k f_o(\omega_{\frac L 2} ^ {k})
\end{aligned}
$$
这样,我们只需求出 $\frac L 2$ 次多项式 $f_e$ 和 $f_o$ 在所有 $\frac L 2$ 次单位根处的取值。
#### 4.3.4 蝴蝶变换
递归处理比较慢,我们希望像位运算卷积一样通过递推实现整个过程。
因为在边界条件下,每个位置的取值与其对应的系数相关,所以递归转递推的关键在于考察系数的变化。
考虑 $n = 8$ 的情况,初始为 $(a_0, a_1, a_2, a_3, a_4, a_5, a_6, a_7)$。
进行第一层递归时,将 $f_e$ 的系数写在左半部分,$f_o$ 的系数写在右半部分,得 $(a_0, a_2, a_4, a_6), (a_1, a_3, a_5, a_7)$。
进行第二层递归时,类似地将每个子问题的 $f_e$ 和 $f_o$ 的系数分别写在左右两侧,得 $(a_0, a_4), (a_2, a_6), (a_1, a_5), (a_3, a_7)$。
进行第三层递归时,共有 $4$ 个大小为 $2$ 的子问题,且进行上述操作后系数的位置不发生改变。
我们看到,如果一个系数在规模为 $2n$ 的问题中的位置为 $p$,若 $p$ 是偶数,则递归至左半部分,若 $p$ 是奇数,则递归至右半部分,且在规模为 $n$ 的问题中的位置为 $\left\lfloor \frac p 2\right\rfloor$。
进一步地,一个系数在第 $i$ 次递归时的方向决定了它最终下标在二进制下第 $w - i(n = 2 ^ w)$ 位的取值。若向左递归则为 $0$,向右递归则为 $1$。而它递归的方向又受到 $\left\lfloor \frac p {2 ^ {i - 1}}\right\rfloor$ 的奇偶性的影响,即 $p$ 在二进制下第 $i$ 位的取值,若为 $0$ 则向左递归,为 $1$ 则向右递归。
这就说明,$p$ 在二进制下第 $i$ 位的取值,等于它对应的系数的最终下标在二进制下第 $w - i$ 位的取值。
因此我们断言,系数 $a_p$ 在 $w$ 次递归后的下标等于 $p$ 二进制翻转后的值,设为 $r_p$。这里翻转指翻转第 $0\sim w - 1$ 位的值。
$r_p$ 可递推求得:$r_0 = 0$。对于 $r_i(i > 0)$,先右移一位得到 $i' = \left\lfloor \frac i 2\right\rfloor$,则 $r_i$ 的低 $w - 1$ 位(第 $0\sim w - 2$ 位)的值可由 $r_{i'}$ 右移一位得到。第 $w - 1$ 位的值只需检查 $i$ 的奇偶性。因此,$r_i = \left\lfloor \frac {r_{i'}}{2} \right\rfloor + \frac n 2(i\bmod 2)$,其中 $i' = \lfloor \frac i 2\rfloor$。
因此,在算法一开始先对系数数组 $a$ 执行 **蝴蝶变换**,即同时令 $a_i \to a_{r_i}$,然后类似 FWT,枚举问题规模 $2d(1\le d < n)$,枚举每个子问题 $2di(0\leq 2di < n)$,再枚举当前子问题的所有对应位置 $(x = 2di + k, y = 2di + k + d)(0\leq k < d)$ 执行变换,即设 $x$ 和 $y$ 对应位置的当前值为 $f_x$ 和 $f_y$,则 $f'_x = f_x + \omega_{2d} ^ k f_y$,$f'_y = f_x - \omega_{2d} ^ k f_y$。
进一步地,根据 $r$ 的定义,我们有 $r_{r_i} = i$。因此,执行蝴蝶变换只需对所有 $i < r_i$ 执行 $\mathrm{swap}(a_i, a_{r_i})$。
这就是 FFT,整个过程称为 **对多项式 $f$ 做长度为 $n$ 的快速傅里叶变换**,时间复杂度 $\mathcal{O}(n\log n)$。代码在 4.5 小节。
#### 4.3.5 DFT 和 FFT
对比 DFT 和 FFT 矩阵:
$$
\mathcal {F_D} =
\begin{bmatrix}
(\omega_N ^ 0) ^ 0 & (\omega_N ^ 0) ^ 1 & \cdots & (\omega_N ^ 0) ^ {N - 1} \\
(\omega_N ^ {-1}) ^ 0 & (\omega_N ^ {-1}) ^ 1 & \cdots & (\omega_N ^ {-1}) ^ {N - 1} \\
\vdots & \vdots & \ddots & \vdots \\
(\omega_n ^ {-(N - 1)}) ^ 0 & (\omega_n ^ {-(N - 1)}) ^ 1 & \cdots & (\omega_N ^ {-(N - 1)}) ^ {N - 1} \\
\end{bmatrix}
\\
\mathcal {F_F} =
\begin{bmatrix}
(\omega_n ^ 0) ^ 0 & (\omega_n ^ 0) ^ 1 & \cdots & (\omega_n ^ 0) ^ {n - 1} \\
(\omega_n ^ 1) ^ 0 & (\omega_n ^ 1) ^ 1 & \cdots & (\omega_n ^ 1) ^ {n - 1} \\
\vdots & \vdots & \ddots & \vdots \\
(\omega_n ^ {n - 1}) ^ 0 & (\omega_n ^ {n - 1}) ^ 1 & \cdots & (\omega_n ^ {n - 1}) ^ {n - 1} \\
\end{bmatrix}
$$
可以发现 DFT 和 FFT 基本一致,它们的差别在于:
- 朴素 FFT 要求 $n$ 是 $2$ 的幂,但 DFT 序列长度可以是任意正整数。
- DFT 和 FFT 带入单位根的顺序是相反的。
注意这些细微差别,不要把 DFT 和 FFT 搞混了。
#### 4.3.6 循环卷积
### 4.4 离散傅里叶逆变换
离散傅里叶逆变换(Inverse Discrete Fourier Transform,IDFT)可以视为单位根处插值的过程。即给出 $n = 2 ^ w$ 个在所有 $n$ 次单位根处的点值 $P_k = (\omega_n ^ k, f(\omega_n ^ k))(0\leq k < n)$,要求还原 $f$ 的各项系数,其中 $f$ 的次数不大于 $n - 1$。
类似地,IDFT 和 IFFT 之间也存在一些差异。想必各位读者根据之前的内容已经可以猜出这种差异是什么了。
#### 4.4.1 范德蒙德方阵逆
考虑范德蒙德方阵
$$
\mathcal A = \begin{bmatrix}
x_0 ^ 0 & x_0 ^ 1 & \cdots & x_0 ^ {n - 1} \\
x_1 ^ 0 & x_1 ^ 1 & \cdots & x_1 ^ {n - 1} \\
\vdots & \vdots & \ddots & \vdots \\
x_{n - 1} ^ 0 & x_{n - 1} ^ 1 & \cdots & x_{n - 1} ^ {n - 1} \\
\end{bmatrix}
$$
这玩意怎么求逆?我们考虑最暴力的方法:拉格朗日插值!
因为范德蒙德方阵可以看成多项式多点求值,根据
$$
\begin{bmatrix}
x_0 ^ 0 & x_0 ^ 1 & \cdots & x_0 ^ {n - 1} \\
x_1 ^ 0 & x_1 ^ 1 & \cdots & x_1 ^ {n - 1} \\
\vdots & \vdots & \ddots & \vdots \\
x_{n - 1} ^ 0 & x_{n - 1} ^ 1 & \cdots & x_{n - 1} ^ {n - 1} \\
\end{bmatrix}
\times
\begin{bmatrix}
a_0 \\ a_1 \\ \vdots \\ a_{n - 1}
\end{bmatrix}
=
\begin{bmatrix}
f(x_0) \\ f(x_1) \\ \vdots \\ f(x_{n - 1})
\end{bmatrix}
$$
再结合拉格朗日插值公式
$$
f(x) = \sum\limits_{i = 0} ^ {n - 1} f(x_i) \prod\limits_{j \neq i} \frac {x - x_j} {x_i - x_j}
$$
可知从 $f(x_j)$ 贡献到 $a_i$ 的系数为 $(\mathcal{A} ^ {-1})_{ij} = [x ^ i] \prod_{k\neq i} \frac {x - x_k} {x_j - x_k}$。
这就是范德蒙德方阵逆当中每个元素的表达式。
#### 4.4.2 算法介绍
很显然,$f$ 在经过快速傅里叶变换后,再进行快速傅里叶逆变换,仍得到 $f$。
因此,只需对快速傅里叶变换的矩阵求逆,即可得到快速傅里叶逆变换的矩阵。
设 $\omega$ 表示 $\omega_n$,则
$$
\mathcal F =
\begin{bmatrix}
(\omega ^ 0) ^ 0 & (\omega ^ 0) ^ 1 & \cdots & (\omega ^ 0) ^ {n - 1} \\
(\omega ^ 1) ^ 0 & (\omega ^ 1) ^ 1 & \cdots & (\omega ^ 1) ^ {n - 1} \\
\vdots & \vdots & \ddots & \vdots \\
(\omega ^ {n - 1}) ^ 0 & (\omega ^ {n - 1}) ^ 1 & \cdots & (\omega ^ {n - 1}) ^ {n - 1} \\
\end{bmatrix}
$$
则 $(\mathcal F ^ {-1})_{ij} = [x ^ i] \prod_{k\neq j} \frac {x - \omega ^ k} {\omega ^ j - \omega ^ k}$。
分子和分母均形如 $g(x) = \frac {\prod_{0\leq k < n} (x - \omega ^ k)} {x - \omega ^ j}$,我们研究该函数的性质。
首先,因为 $\omega ^ k(0\leq k < n)$ 为 $x ^ n - 1 = 0$ 的 $n$ 个互不相同的根,根据因式定理,$\prod_{0\leq k < n} (x - \omega ^ k)$ 就等于 $x ^ n - 1$。感性理解:将 $\prod_{0\leq k < n} (x - \omega ^ k)$ 展开,再应用单位根的 **对称性**。
模拟短除法 $\frac {x ^ n - 1} {x - \omega ^ j}$,可知
$$
g(x) = x ^ {n - 1} + \omega ^ jx ^ {n - 2} + (\omega ^ j) ^ 2x ^ {n - 3} + \cdots + (\omega ^ j) ^ {n - 1} x ^ 0
$$
因此
$$
(\mathcal F ^ {-1})_{ij} = \frac {[x ^ i] g(x)} {g(\omega ^ j)} = \frac {(\omega ^ j) ^ {n - 1 - i}} {n(\omega ^ j) ^ {n - 1}} = \frac {(\omega ^ {-j}) ^ {i}\omega ^ {-j}} {n\omega ^ {-j}} = \frac {\omega ^ {-ij}} {n}
$$
这就说明
$$
\mathcal F ^ {-1} =
\frac 1 n
\begin{bmatrix}
(\omega ^ {-0}) ^ 0 & (\omega ^ {-0}) ^ 1 & \cdots & (\omega ^ {-0}) ^ {n - 1} \\
(\omega ^ {-1}) ^ 0 & (\omega ^ {-1}) ^ 1 & \cdots & (\omega ^ {-1}) ^ {n - 1} \\
\vdots & \vdots & \ddots & \vdots \\
(\omega ^ {-(n - 1)}) ^ 0 & (\omega ^ {-(n - 1)}) ^ 1 & \cdots & (\omega ^ {-(n - 1)}) ^ {n - 1} \\
\end{bmatrix}
$$
因此,对一个序列做 IFFT,只需将 FFT 递归公式里面的 $\omega_L ^ k$ 换成 $\omega_L ^ {-k}$,并在最后将所有数除以 $n$ 即可。
这就引出了 IDFT 公式及其对应矩阵:
$$
x_n = \frac 1 N \sum_{k = 0} ^ {N - 1} X_k e ^ {\frac {2\pi i} Nkn} = \sum_{k = 0} ^ {N - 1} X_k \omega_N ^ {kn} \\
\mathcal {F_D} ^ {-1} =
\frac 1 N
\begin{bmatrix}
(\omega_N ^ 0) ^ 0 & (\omega_N ^ 0) ^ 1 & \cdots & (\omega_N ^ 0) ^ {N - 1} \\
(\omega_N ^ 1) ^ 0 & (\omega_N ^ 1) ^ 1 & \cdots & (\omega_N ^ 1) ^ {N - 1} \\
\vdots & \vdots & \ddots & \vdots \\
(\omega_N ^ {N - 1}) ^ 0 & (\omega_N ^ {N - 1}) ^ 1 & \cdots & (\omega_N ^ {N - 1}) ^ {N - 1} \\
\end{bmatrix}
$$
### 4.5 快速多项式乘法
通过 FFT 和 IFFT,我们可以在 $\mathcal{O}(n\log n)$ 的时间内实现 $n - 1$ 次多项式在系数表示法和点值表示法之间的转换。
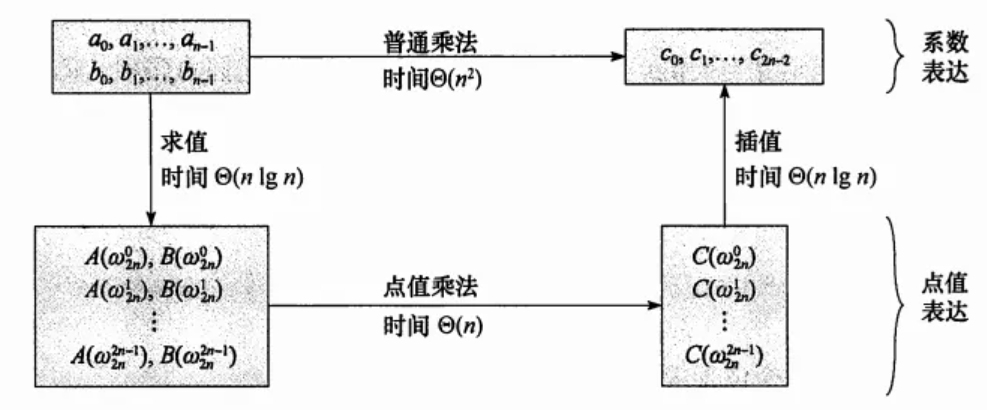
计算两个次数分别为 $n - 1$ 和 $m - 1$ 的多项式 $a, b$ 相乘,设结果为 $c$,则 $c$ 是 $n + m - 2$ 次多项式,我们需要 $n + m - 1$ 个点值才能确定它。根据点值的性质,首先找到不小于 $n + m - 1$ 的最小的 $2$ 的幂 $L$,对系数表示法的 $a, b$ 分别做长度为 $L$ 的 FFT,将对应点值相乘得到 $\hat c$,再对 $\hat c$ 做 IFFT 还原 $c$。
---
首先我们需要实现一个复数类,它支持复数的加减乘运算。也可以使用 C++ 自带复数类 `std::complex<T>`,用法见 [CPP reference](https://zh.cppreference.com/w/cpp/numeric/complex)。
FFT 和 IFFT 大体上一致,只有一些细小差别。我们可以类似实现 FWT 和 IFWT 那样,用同一个函数实现它们,并用一个参数区别。
等式 $\omega_n = \cos(\frac {2\pi} {n}) + i\sin(\frac {2\pi} {n})$ 帮助我们求出 $n$ 次单位根。
- **注意浮点数的精度**。当多项式系数的绝对值较大时,需使用 `long double` 甚至 5.2 小节的任意模数卷积。
模板题 [P3803](https://www.luogu.com.cn/problem/P3803) 代码:
```cpp
#include <bits/stdc++.h>
using namespace std;
constexpr int N = 1 << 21;
constexpr double pi = acos(-1);
struct comp {
double a, b; // a + bi
comp operator + (const comp &x) const {return {a + x.a, b + x.b};}
comp operator - (const comp &x) const {return {a - x.a, b - x.b};}
comp operator * (const comp &x) const {return {a * x.a - b * x.b, a * x.b + b * x.a};}
} f[N], g[N], h[N];
int n, m, r[N];
void FFT(int L, comp *f, bool type) { // L 表示长度, type = 1 表示 FFT, type = 0 表示 IFFT
for(int i = 1; i < L; i++) {
r[i] = (r[i >> 1] >> 1) + (i & 1 ? L >> 1 : 0);
if(i < r[i]) swap(f[i], f[r[i]]);
}
for(int d = 1; d < L; d <<= 1) {
comp wd = {cos(pi / d), sin(pi / d)}; // 2d 次单位根
if(!type) wd.b = -wd.b; // IFFT 单位根取倒数, 相当于沿 x 轴对称
static comp w[N];
w[0] = {1, 0};
for(int j = 1; j < d; j++) w[j] = w[j - 1] * wd; // 用数组记录 0 ~ d-1 次单位根, 减少复数乘法次数
for(int i = 0; i < L; i += d << 1) {
for(int j = 0; j < d; j++) {
comp x = f[i | j], y = w[j] * f[i | j | d];
f[i | j] = x + y, f[i | j | d] = x - y;
}
}
}
if(!type) for(int i = 0; i < L; i++) f[i].a /= L; // IFFT 时所有数要除以长度 L, 我们只用到了实部所以只需将实部除以 L
}
int main() {
cin >> n >> m;
for(int i = 0; i <= n; i++) cin >> f[i].a;
for(int i = 0; i <= m; i++) cin >> g[i].a;
int L = 1;
while(L <= n + m) L <<= 1;
FFT(L, f, 1), FFT(L, g, 1);
for(int i = 0; i < L; i++) h[i] = f[i] * g[i];
FFT(L, h, 0);
for(int i = 0; i <= n + m; i++) cout << (int) (h[i].a + 0.5) << (i < n + m ? ' ' : '\n');
return 0;
}
```
### 4.6 快速数论变换
前置知识:原根和阶。
我们将 DFT 的数值范围从复数域推广至任意存在 $n$ 次单位根 $\alpha$ 的环 $R$,其中 $\alpha$ 满足 $\alpha ^ k(0\leq k < n)$ 互不相同,对 $x_0, x_1, \cdots, x_{n - 1}$ DFT 得 $X_0, X_1, \cdots, X_{n - 1}$,则
$$
X_i = \sum_{j = 0} ^ {n - 1} x_j \alpha ^ {ij}
$$
也可以视作 $X_i = f(\alpha ^ i)$,其中 $f(t) = \sum_{j = 0} ^ {n - 1} x_j t ^ j$。
类似可知 IDFT
$$
x_j = \frac 1 n \sum_{i = 0} ^ {n - 1} X_i \alpha ^ {-ij}
$$
即 DFT 和 IDFT 对序列进行的变换的本质抽象。
#### 4.6.1 算法介绍
快速数论变换即在模 $p$ 意义下的整数域 $F = \mathbb Z / p$ 进行的快速傅里叶变换。
设变换长度为 $n$,则需存在 $n$ 次单位根 $a$ 满足 $\delta_p(a) = n$。大部分题目的模数 $p$ 满足:
- $p$ 为质数。
- $2 ^ k\mid p - 1$,其中 $2 ^ k$ 不小于最大的可能的 NTT 长度。
第一条性质保证 $p$ 存在原根 $g$ 且 $n$ 可逆,第二条性质保证存在 $n$ 次单位根。注意它不是充要条件,只是充分条件。
根据原根的性质,$\delta_p(g) = p - 1$,即 $g$ 的 $0\sim p - 2$ 次幂互不相同,则 $g$ 在 $F$ 上的性质和复数域上 $p - 1$ 次单位根的性质完全一致:$g ^ k(0\leq k < p - 1)$ 和 $\omega_{p - 1} ^ k(0\leq k < p - 1)$ 形成的域是同构的,$g ^ k$ 等价于 $\omega_{p - 1} ^ k$。
因此,$q = g ^ {\frac {p - 1} {n}}$ 等价于 $\omega_{p - 1} ^ {\frac {p - 1} n}$ 即 $\omega_n$,它的 $0\sim n - 1$ 次幂互不相同,即 $\delta_p(q) = n$,也可以通过阶的性质 $\delta_p(g ^ k) = \frac {\delta_p(g)} {\gcd(\delta_p(g), k)}$ 说明。
常见 NTT 模数有:
- $998244353 = 7\times 17 \times 2 ^ {23} + 1$,有原根 $3$。它可以用来做长度不超过 $2 ^ {23}$ 的 NTT,也是最常见的模数。
- $1004535809 = 479 \times 2 ^ {21} + 1$,有原根 $3$。
- $469762049 = 7 \times 2 ^ {26} + 1$,有原根 $3$。
如果不是常见模数,我们需要检验 $p$ 是否为形如 $q2 ^ k + 1$ 的质数,$2 ^ k$ 是否足够大,再运用原根相关的知识枚举并判定找到任意一个原根,就可以做 NTT 了。
注意以上只是模数 $p$ 可 NTT 的充分条件,它的更弱的条件是存在 $\delta_{p}(a) = n$ 和 $n ^ {-1}$。如果 NTT 是正解的一部分,那么一个合格的出题人应将 $p$ 设为常见模数,因为模数不是考察重点。
#### 4.6.2 代码实现
朴素 NTT 已经比 FFT 快了不少,因为复数运算很耗时。
接下来加入一些常数优化:
- 预处理 $2d$ 次单位根的 $0\sim d - 1$ 次幂,这样对每个 $i$ 枚举 $j$ 的时候就不需要重复计算单位根的幂。
- 用 `unsigned long long` 和 $16$ 次模一次的技巧,减少取模次数。类似技巧也用于优化矩阵乘法。
综上,写出如下代码(依然是 [模板题](https://www.luogu.com.cn/problem/P3803)):尽管题目没有要求取模,但可视为在模 $p$ 意义下进行多项式乘法,其中 $p$ 大于答案的每一项。
```cpp
#include <bits/stdc++.h>
using namespace std;
using ull = unsigned long long;
constexpr int N = 1 << 21;
constexpr int mod = 998244353;
constexpr int ivg = (mod + 1) / 3;
int ksm(int a, int b) {
int s = 1;
while(b) {
if(b & 1) s = 1ll * s * a % mod;
a = 1ll * a * a % mod, b >>= 1;
}
return s;
}
int n, m, r[N], f[N], g[N], h[N];
void FFT(int L, int *a, bool type) {
static ull f[N], w[N];
for(int i = 0; i < L; i++) f[i] = a[r[i] = (r[i >> 1] >> 1) | (i & 1 ? L >> 1 : 0)];
for(int d = 1; d < L; d <<= 1) {
int wd = ksm(type ? 3 : ivg, (mod - 1) / (d + d));
for(int j = w[0] = 1; j < d; j++) w[j] = 1ll * w[j - 1] * wd % mod;
for(int i = 0; i < L; i += d << 1) {
for(int j = 0; j < d; j++) {
int y = w[j] * f[i | j | d] % mod;
f[i | j | d] = f[i | j] + mod - y, f[i | j] += y;
}
}
if(d == (1 << 16)) for(int p = 0; p < L; p++) f[p] %= mod;
}
int inv = ksm(L, mod - 2);
for(int i = 0; i < L; i++) a[i] = f[i] % mod * (type ? 1 : inv) % mod;
}
int main() {
cin >> n >> m;
for(int i = 0; i <= n; i++) cin >> f[i];
for(int i = 0; i <= m; i++) cin >> g[i];
int L = 1;
while(L <= n + m) L <<= 1;
FFT(L, f, 1), FFT(L, g, 1);
for(int i = 0; i < L; i++) h[i] = 1ll * f[i] * g[i] % mod;
FFT(L, h, 0);
for(int i = 0; i <= n + m; i++) cout << h[i] << (i < n + m ? ' ' : '\n');
return 0;
}
```
## 5. 应用与技巧
FFT 和 NTT 是所有快速多项式操作的基础。
设多项式 $f$ DFT 得到 $\hat f$,也记为 $\operatorname {DFT}(f)$。可以发现,**DFT 是线性变换**,因此它具有 **线性性**,这是它最重要且最常用的一个性质:
- $c \operatorname {DFT}(f) + d \operatorname {DFT}(g) = \operatorname {DFT} (cf + dg)$。
### 5.1 常数优化
在分析变换次数的时候,一般不区分 DFT 和 IDFT。
#### 5.1.1 三次变两次优化
计算两 **实系数** 多项式 $f, g$ 相乘。
根据 $(a + bi) ^ 2 = (a ^ 2 - b ^ 2) + 2abi$,将 $f + gi$ 平方后取出虚部再除以 $2$ 即可。
这样,三次 DFT 变成了两次 DFT,对常数有显著优化。[代码](https://uoj.ac/submission/597211)。
这个优化被接下来稍复杂的技巧完全包含,它们的核心思想都是利用实系数的性质。
#### 5.1.2 合并两次实系数 DFT
同时计算两 **实系数** 多项式 $f, g$ 的 DFT。
类似地,我们设 $u = f + ig$,$v = f - ig$。先求出 $u$ 的 DFT $\hat u$,考虑能否利用 $\hat u$ 直接求出 $\hat v$。
在给出做法之前,我们还要引入一些复数相关的概念:
- 定义:对于两个复数 $z_1$ 和 $z_2$,若它们实部相等,虚部互为相反数,则称 $z_1, z_2$ 互为 **共轭复数**。$z_2$ 是 $z_1$ 的共轭,$z_1$ 是 $z_2$ 的共轭。
- 表示:复数 $z$ 的共轭记作 $\overline {z}$ 或 $\operatorname {conj}(z)$。
- 运算性质:两个共轭复数的辐角互为相反数,即 $\arg z_1 = -\arg z_2$。根据棣莫弗定理,可知 **复数积的共轭,等于它们共轭的积**。这样理解:求共轭相当于把整个复平面沿 $x$ 轴翻转,求积再翻转等价于翻转再求积。
- 易知复数和的共轭等于它们共轭的和,且一个复数的共轭的共轭等于它本身。
首先,$v(\omega_n ^ k) = \sum_{i = 0} ^ {n - 1} v_i(\omega_n ^ k) ^ i$。为了让它和 $u$ 产生联系,因为 $f, g$ 为实系数多项式,所以 $u$ 和 $v$ 的各项系数互为共轭,我们对整个结果求两次共轭,并将一次共轭根据共轭的性质下放至 $v_i$ 和 $\omega_n ^ k$。
$$
\begin{aligned}
\hat v_k
& = v(\omega_n ^ k) \\
& = \sum_{i = 0} ^ {n - 1} v_i(\omega_n ^ k) ^ i \\
& = \operatorname {conj} \left( \operatorname {conj} \left(\sum_{i = 0} ^ {n - 1} v_i(\omega_n ^ k) ^ i \right) \right) \\
& = \operatorname {conj} \left( \sum_{i = 0} ^ {n - 1} \operatorname {conj}(v_i(\omega_n ^ k) ^ i) \right) \\
& = \operatorname {conj} \left( \sum_{i = 0} ^ {n - 1} \operatorname {conj}(v_i)\operatorname {conj}(\omega_n ^ k) ^ i \right) \\
& = \operatorname {conj} \left( \sum_{i = 0} ^ {n - 1} \operatorname {conj}(v_i)\operatorname {conj}(\omega_n ^ k) ^ i \right) \\
& = \operatorname {conj} \left( \sum_{i = 0} ^ {n - 1} u_i (\omega_n ^ {n - k}) ^ i \right) \\
& =
\begin{cases}
\operatorname {conj} (\hat u ^ {n - k}) & (1\leq k < n) \\
\operatorname {conj} (\hat u_0) & (k = 0)
\end{cases}
\end{aligned}
$$
求得 $\hat v$ 之后,因为 $\hat u = \hat f + i\hat g$,$\hat v = \hat f - i\hat g$,所以 $\hat f = \frac {\hat u + \hat v} {2}$,$\hat g = \frac {\hat u - \hat v} {2i} = \frac {(\hat v - \hat u)i} {2}$。
#### 5.1.3 合并两次实系数 IDFT
这里实系数指 IDFT 后的各项系数为实数。如果是 IDFT 前的各项系数为实数,直接使用上一小节的技巧即可。
设需要 IDFT 的两个多项式为 $\hat f$ 和 $\hat g$。计算 $\operatorname {IDFT}(\hat f)$,各项系数均为实数,虚部信息被浪费了。考虑计算 $\operatorname {IDFT}(\hat f + i\hat g)$,则各项系数的实部即 $f$ 的系数,虚部即 $g$ 的系数。
### 5.2 任意模数卷积
给定两多项式 $f, g$,在系数模 $p$ 意义下求出它们的卷积 $h = f * g$。
若 $p$ 不是 NTT 模数,我们不能朴素地使用 FFT 求解该问题,因为 $h$ 的系数可达 $n p ^ 2$。取 $n = 10 ^ 6$,$p = 10 ^ 9$,则 $np ^ 2 = 10 ^ {24}$,`long double` 也无法接受。
接下来介绍两种常见的解决该问题的方法。它们也被称为 MTT(非正式),得名于毛啸 2016 年的集训队论文。
#### 5.2.1 拆系数 FFT
设 $B = \sqrt p$,将所有系数表示为 $kB + r(0\leq r < B)$ 的形式,得到四个多项式 $f = f_0B + f_1$,$g = g_0B + g_1$,计算它们两两相乘的结果,则 $fg = (f_0g_0) B ^ 2 + (f_0g_1 + f_1g_0)B + f_1g_1$。
显然有一个四次 DFT 和三次 IDFT 的朴素做法:对 $f_0, f_1, g_0, g_1$ 进行 DFT,$\hat f_0\cdot \hat g_0, \hat f_0\cdot \hat g_1 + \hat f_1\cdot \hat g_0, \hat f_1 \cdot \hat g_1$ 进行 IDFT。
使用 6.1.2 和 6.1.3 的技巧,可以做到两次 DFT 和两次 IDFT。系数值域 $nB ^ 2 = np = 10 ^ {15}$,勉强可以接受。
模板题 [P4245 任意模数多项式乘法](https://www.luogu.com.cn/problem/P4245) 的 [代码](https://uoj.ac/submission/597614)。注意用 `long double`,`double` 会被卡精度,或者换一种精度较高的 FFT [写法](https://uoj.ac/submission/597615)。
#### 5.2.2 三模数 NTT
前置知识:(扩展)中国剩余定理。
选取三个常用 NTT 模数,分别算出 $f * g$ 在这些模数下的结果,再使用中国剩余定理合并即可。
我们选择 $p_1 = 998244353$,$p_2 = 1004535809$ 和 $p_3 = 469762049$,设结果分别为 $h_1, h_2, h_3$。
如果使用 CRT,则需要 `__int128`,因为 $h$ 的真实值为
$$
(h_1p_2p_3\times \mathrm{inv}(p_2p_3, p_1) + h_2p_1p_3\times \mathrm{inv}(p_1p_3, p_2) + h_3p_1p_2\times \mathrm{inv}(p_1p_2, p_3)) \bmod (p_1p_2p_3)
$$
使用 exCET 就不需要 `__int128`:
- 合并 $h\equiv h_1\pmod {p_1}$ 和 $h\equiv h_2\pmod {p_2}$。设 $h = h_1 + yp_1$,则 $h_1 + yp_1 \equiv h_2\pmod {p_2}$,解得 $y\in [0, p_2)$ 之后得到 $h \equiv h_1 + yp_1 \pmod {p_1p_2}$,记作 $h\equiv x\pmod {p_1p_2}$。
- 合并 $h \equiv x\pmod {p_1p_2}$ 和 $h\equiv h_3 \pmod {p_3}$。设 $h = x + yp_1p_2$,类似解得 $y\in [0, p_3)$,得到 $h \equiv x + yp_1p_2\pmod {p_1p_2p_3}$。因为 $x + yp_1p_2 < p_1p_2p_3$,所以它就是真实值,可以直接取模。
效率比拆系数 FFT 低不少,因为进行了九次 DFT。[代码](https://uoj.ac/submission/597639)。
### 5.3 分治 NTT
前置知识:CDQ 分治。
分治 NTT 在信息竞赛界应用广泛,这归功于他所解决的问题:形如 $f_i = \sum_{j = 0} ^ {i - 1} f_j g_{i - j}$ 的 **半在线卷积**。
#### 5.3.1 算法介绍
形如给定 $g_1\sim g_{n - 1}$ 和 $f_0$,求 $f_1\sim f_{n - 1}$ 满足 $f_i = \sum_{j = 0} ^ {i - 1} f_j g_{i - j}$ 的问题被称为 **半在线卷积**。因为 $f_i$ 很大,一般会对 NTT 模数 $p$ 取模。
我们不能通过简单的 NTT 解决这个问题,因为 $f$ 的每一项均和之前项有关,这要求我们在尝试计算 $f_i$ 时必须已经求出 $f_0\sim f_{i - 1}$,而 NTT 做不到这一点。或者说,它们解决的问题形式不同。
这是一个在线的问题,考虑使用 **CDQ 分治** 转化为静态问题。
- 设当前分治区间为 $[l, r]$,其中 $f_0 \sim f_{l - 1}$ 对 $f_l\sim f_r$ 的贡献已经计算完毕。
- 若 $l = r$,说明已经求出 $f_l$,返回。
- 否则,令 $m = \lfloor \frac {l + r} 2\rfloor$,先向左递归 $[l, m]$ 求解 $f_l\sim f_m$。
- 为了求解 $f_{m + 1}\sim f_r$,我们需要计算 $f_l\sim f_m$ 对它们的贡献:$f_i = \sum_{j = l} ^ m f_j g_{i - j}$。因为 $f_l\sim f_m$ 已知,所以总的贡献相当于两个已知的多项式相乘的结果。具体地,令 $f'_j = f_{j + l}(0\leq j \leq m - l)$,计算 $h = f' * g$,则 $f_i$ 受到 $h_{i - l}$ 的贡献。
- 向右递归 $[m + 1, r]$ 求解 $f_{m + 1}\sim f_r$。
因为 $f, g$ 的长度均不超过区间长度,所以时间复杂度 $\mathcal{O}(n\log ^ 2 n)$。
模板题 [P4721 分治 FFT](https://www.luogu.com.cn/problem/P4721) 代码:
```cpp
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using ull = unsigned long long;
constexpr int N = 1 << 17;
constexpr int mod = 998244353;
void add(int &x, int y) {x += y, x >= mod && (x -= mod);}
int ksm(int a, int b) {
int s = 1;
while(b) {
if(b & 1) s = 1ll * s * a % mod;
a = 1ll * a * a % mod, b >>= 1;
}
return s;
}
int n, f[N], g[N];
void solve(int l, int r) {
if(l == r) return;
int m = l + r >> 1, L = 1;
solve(l, m);
while(L < r - l + 1) L <<= 1;
static int a[N], b[N], c[N];
memset(a, 0, L << 2);
memcpy(a, f + l, m - l + 1 << 2);
memcpy(b, g, L << 2);
NTT(L, a, 1), NTT(L, b, 1);
for(int i = 0; i < L; i++) c[i] = 1ll * a[i] * b[i] % mod;
NTT(L, c, 0);
for(int i = m + 1; i <= r; i++) add(f[i], c[i - l]);
solve(m + 1, r);
}
int main() {
cin >> n;
for(int i = 1; i < n; i++) scanf("%d", &g[i]);
f[0] = 1, solve(0, n - 1);
for(int i = 0; i < n; i++) printf("%d%c", f[i], i + 1 < n ? ' ' : '\n');
return 0;
}
```
#### 5.3.2 阶梯网格路径计数
阶梯网格路径计数是一类可以使用分治 NTT 解决的经典问题。
给定 $n + 1$ 列 $m + 1$ 行的网格图,左下角和右上角分别记为 $(0, 0)$ 和 $(n, m)$。从 $(0, 0)$ 出发,每次只能向右或向上走,求走到 $(n, m)$ 的方案数。让我们回忆:方案数为 $\binom {n + m} n$。
当然,问题没有这么简单。我们限制第 $i$ 列不能走到行数大于 $c_i$ 的点,其中 $c_i$ 单调不降,且 $c_n = m$。换言之,求出在一个阶梯网格从左下角走到右上角的方案数。
显然有 $\mathcal{O}(nm)$ 的动态规划:设 $f_{i, j}$ 表示走到 $(i, j)$ 的方案数,则 $f_{i, j}$ 转移至 $f_{i + 1, j}$ 和 $f_{i, j + 1}$。
考虑一段 $c_i$ 相同的极长区间 $[l, r](l < r)$ 从 $f_{l, j_1}$ 转移到 $f_{r, j_2}$ 的贡献系数:为防止重复计数,从 $(l, j_1)$ 出发的第一步应当向右,因此有系数 $\binom {(r - l - 1) + (j_2 - j_1)} {r - l - 1}$。设 $g_i$ 表示 $\binom {r - l - 1 + i} {i}$,则 $f_{l, j_1} g_i\to f_{r, j_1 + i}$,为卷积形式。
在不受 $c_i$ 影响的时候,我们确实可以这样做。但是对于每个 $i$,它内层的所有 $j$ 之间也有转移,这让我们不方便借助分治和卷积加快整个过程。考虑进行一些等价转换便于分层。
稍作思考,设 $f_{k, j}$ 表示走到 $(i, j)$ 其中 $i + j = k$ 的方案数,则 $f_{k, j}$ 转移至 $f_{k + 1, j}$ 和 $f_{k + 1, j + 1}$。
进一步地,为了避免在 $k > n$ 时受到 $j\geq k - n$ 的限制,考虑从 $(n, 0)$ 开始沿左上方向把整个阶梯网格劈成两半,分别计算从 $(0, 0)$ 和 $(n, m)$ 到斜对角线上的点($i + j = n$)的方案数,而这两个问题是对称的。
综合上述分析,我们将问题转化为:从 $(0, 0)$ 出发,每次可以向右或右上走一步,求走到最右侧一列每个点的方案数。其中,在第 $i$ 列不能走到行数大于 $c_i$ 的点。这个 $c_i$ 可通过原问题的 $c_i$ 进行简单转化得到,且容易证明其仍不降且满足很好的性质:$c_{i + 1} - c_i \leq 1$。
因此,从 $f_l$ 推到 $f_r$ 的时候,我们会发现对于 $j\leq c_r - (r - l)$,设不等号右侧的数为 $x$,$f_{l, j}$ 对 $f_r$ 的贡献不会受到 $c$ 的影响:因为 $c_{i + 1} - c_i\leq 1$,所以从 $(l, j)$ 开始,就算每一步都往右上走,也不会突破限制。这样,$f_{l, 0}\sim f_{l, x}$ 对 $f_r$ 的贡献可直接卷积计算。对于 $f_{l, x + 1}\sim f_{l, c_l}$,分治下放至左右子区间 $(l, m]$ 和 $(m, r]$ 进行递归。
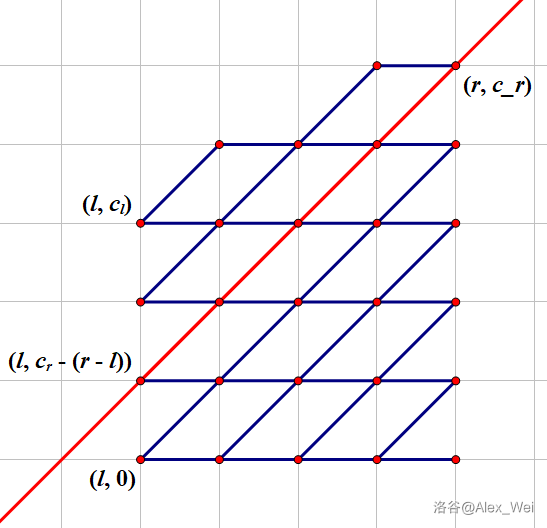
有了大致思路,设计算法就很简单了:设 $\mathrm{solve}(l, r, \Delta, F)$ 表示当前区间为 $(l, r]$,传入多项式 $F$ 的第 $i$ 项表示 $f_{l, i + \Delta}$,返回多项式 $G$ 的第 $i$ 项表示 $f_{r, i + \Delta}$。也可视作暂时将 $c_l\sim c_r$ 全部减去 $\Delta$,传入 $f_l = F$,返回 $G = f_r$,接下来就使用这种视角。
对于 $j \leq c_r - (r - l)$,设不等号右侧的数为 $x$,$F_0\sim F_x$ 和 $H_0\sim H_{r - l}$ 卷积求出 $F_0\sim F_x$ 转移得到的 $G_0\sim G_{c_r}$,其中 $H_i$ 即转移系数 $\binom {r - l} i$。
对于 $j > x$,分治下放:设 $F' = F_{x + 1}\sim F_{c_l}$,$mid = \lfloor \frac {l + r} {2} \rfloor$,则先递归左半部分 $F'\gets \mathrm{solve}(l, mid, \Delta + x + 1, F')$,再递归右半部分 $F'\gets \mathrm{solve}(mid, r, \Delta + x + 1, F')$,则此时 $F'$ 表示从 $F_{x + 1}\sim F_{c_l}$ 转移得到的 $G_{x + 1}\sim G_{c_r}$。
两部分相加即得 $G$,返回即可。
边界 $r - l = 1$ 的处理是平凡的。
两次下传 $F'$ 时,$F'$ 的长度显然不超过 $c_r - x = r - l$,因此在处理区间 $(l, r]$ 时涉及到的所有多项式的长度均不超过其父区间长度。设 $n, m$ 同级,则时间复杂度为 $\mathcal{O}(n\log ^ 2 n)$。
接下来对问题进行一些扩展:
- 如果没有 $c_{i + 1} - c_i\leq 1$ 的性质,但 $c_i$ 单调不降,还能做吗?答案是可以,只需将 $x$ 的定义改为 $c_l - (r - l)$,此时 $(l, r]$ 涉及到的多项式长度不超过父区间的长度加上端点处 $c$ 的差值,可以接受。
### 5.4 例题
#### [CF1770G Koxia and Bracket](https://www.luogu.com.cn/problem/CF1770G)
相比于 F,这道题就略显套路了。
将左括号视为 $1$,右括号视为 $-1$,找到最后一个使得前缀和小于 $0$ 的位置 $lst$,则 $s_1\sim s_{lst}$ 的每个左括号都有用,必然不会删去。同理,$s_{lst + 1}\sim s_n$ 的每个右括号也都有用。
对于 $s_1\sim s_{lst}$ 的每个右括号 $s_i$,如果它对应的前缀和为 $c_i$,则为保证前缀和非负,在 $s_1\sim s_i$ 中至少需要删掉 $-c_i$ 个右括号。我们只关心 $-c_i$ 的前缀最大值,因为若这些位置满足条件,则所有位置满足条件,而每个前缀最大值一定会比先前的前缀最大值大 $1$,所以我们将问题转化为:给定长为 $m$ 的序列,其中有 $c$ 个位置被打上了标记,求出选择 $c$ 个位置的方案数,使得对于每个前缀,选择的位置数不小于被打上标记的位置数。
设 $f_{i, j}$ 表示考虑到第 $i$ 个位置,当前选择位置数减去打标记位置数的数量为 $j$。对于没有被打标记的位置 $p$,$f_{p - 1, j}$ 转移到 $f_{p, j / j + 1}$,否则转移到 $f_{p, j - 1 / j}$。
非常明显的阶梯格路计数问题,稍有变形,不过解法大差不差,核心思想是一致的:考虑 $f_l$ 转移到 $f_r$,用卷积描述一部分转移,剩下来 $\mathcal{O}(r - l)$ 个位置分别递归两侧处理。
对于本题,就是 $f_{l, j}(j\geq cnt)$ 对 $f_r$ 的贡献用卷积描述,其中 $cnt$ 表示 $l + 1\sim r$ 的被打上标记的位置。剩余部分递归,长度只有 $cnt$,而且因为截取的是低位,我们甚至不需要记录偏移量 $\Delta$。
$r - l = 1$ 的边界情况是平凡的。
$s_{lst + 1}\sim s_n$ 的左括号类似处理即可。
每个分治区间涉及到的多项式长度不超过其父区间长度,因此时间复杂度为 $\mathcal{O}(n\log ^ 2n)$。[代码](https://codeforces.com/contest/1770/submission/188373663)。
## 参考资料
第一章:
- [复数 - OI Wiki](https://oi-wiki.org/math/complex/)。
- [复数 - 百度百科](https://baike.baidu.com/item/复数/254365)。
- [Video] [虚数的来源 - Veritasium](https://www.bilibili.com/video/BV11h411x7z5/)。
- [Video] [【官方双语】微分方程概论 - 第五章:在 3.14 分钟内理解 $e ^ {i\pi}$ - 3Blue1Brown](https://www.bilibili.com/video/BV1G4411D7kZ/)。
第二章:
- [多项式与生成函数简介 - OI Wiki](https://oi-wiki.org/math/poly/intro/)。
- [多项式 - 百度百科](https://baike.baidu.com/item/多项式/10660961)。
- [代数基本定理 - OI Wiki](https://oi-wiki.org/math/poly/fundamental/)。
第四章:
- [快速傅里叶变换 - OI Wiki](https://oi-wiki.org/math/poly/fft/)。
- [FFT 理性瞎扯 - xtx1092515503](https://www.luogu.com.cn/blog/Troverld/fft-li-xing-xia-che)。
- [Vandermonde matrix - Wikipedia](https://en.wikipedia.org/wiki/Vandermonde_matrix)。
- [Discrete Fourier transform - Wikipedia](https://en.wikipedia.org/wiki/Discrete_Fourier_transform)。
- [浅谈范德蒙德 (Vandermonde) 方阵的逆矩阵的求法以及快速傅里叶变换 (FFT) 中 IDFT 的原理 - Deadecho](https://www.cnblogs.com/gzy-cjoier/p/9741950.html)。
- [范德蒙德矩阵的逆矩阵怎么计算? - FFjet 的回答 - 知乎](https://www.zhihu.com/question/309243881/answer/575306025)。
- [Discrete Fourier transform over a ring - Wikipedia](https://en.wikipedia.org/wiki/Discrete_Fourier_transform_over_a_ring#Number-theoretic_transform)。
- [NTT 与多项式全家桶 - command_block](https://www.luogu.com.cn/blog/command-block/ntt-yu-duo-xiang-shi-quan-jia-tong)。
- [Video] [这个算法改变了世界 - Veritasium](https://www.bilibili.com/video/BV1CY411R7bA/)。
- [Video] [The Fast Fourier Transform (FFT): Most Ingenious Algorithm Ever? - Reducible](https://www.youtube.com/watch?v=h7apO7q16V0) & [B 站搬运](https://www.bilibili.com/video/BV1za411F76U/)。
第五章:
- [P3803 题解 - NaCly_Fish](https://www.luogu.com.cn/blog/NaCly-Fish-blog/solution-p3803)。
- 2016 集训队论文《再探快速傅里叶变换》—— 毛啸。