题目传送
blog 食用
本题解目前提供 hash 和 SA 做法。
一、分析
推结论
首先进行题意分析,题目要求最短的 t,直接枚举 t 肯定是不现实的,所以要对 s 进行处理。
所以我们来分析样例:
qwq → qwqwq
lingluo → lingluolingluo
aaaaaaabaa → aaaaaaabaaaaaaabaa
发现两个样例中间都有重复的部分,所以我们用括号标出中间用了两次的部分,如下:
qwq → qw(q)wq
lingluo → lingluo()lingluo
aaaaaaabaa → aaaaaaab(aa)aaaaabaa
不难发现,括出来的部分是 s 的最长 border,也就是求一个最长的串 s'(可以为空)使 s' 既是 s 的前缀,又是 s 的后缀,且不为 s,这样这个 s' 就可以用两次。(这个是后面说的假设)
## 二、证明
### 1. 证明 $s$ 是 $t$ 的 border
因为 $s'$ 为 $s$ 的前缀,所以可令 $s=s'+s''$,于是 $t=s-s'+s=s-s'+s'+s''=s+s''$,满足 $s$ 是 $t$ 的前缀。
又因为 $s'$ 为 $s$ 的后缀,所以可令 $s=s'''+s'$,于是 $t=s-s'+s=s'''+s'-s'+s=s'''+s$,满足 $s$ 是 $t$ 的后缀。
所以 $s$ 是 $t$ 的 border。
### 2. 证明 $t$ 是满足条件的最短的
如果有比 $t$ 更短的 $r$ 满足条件,设中间用两次的部分为 $r'$,那么 $r'$ 会长于 $s'$,且 $r'$ 既是 $s$ 的前缀,又是 $s$ 的后缀,如图,与假设矛盾。
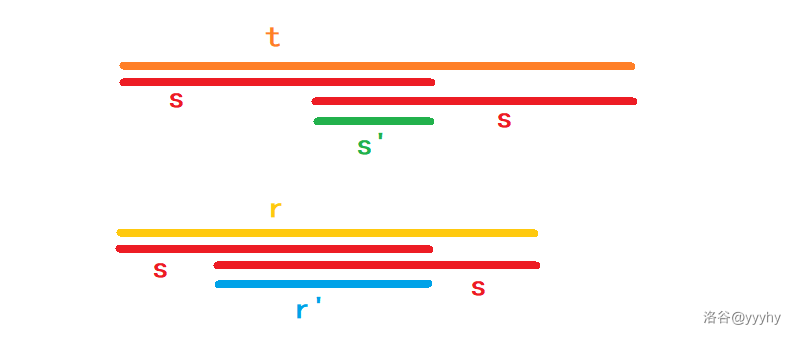
### 3. 证明 $s$ 是 $t$ 最长的 border
若存在更长的 $q$ 是 $t$ 的 border,那么可令 $t=q+q''=q'''+q$。
于是如图:
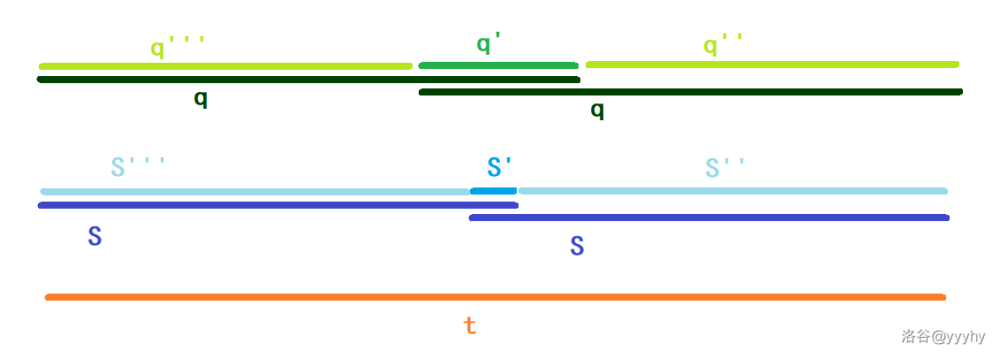
然后记 $q'$ 左端点到 $s'$ 右端点这一段为 $p$,那么如下图推断:
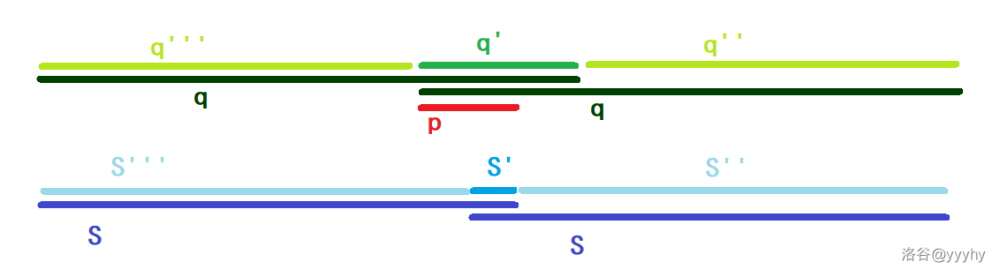
通过 $q$ 转换位置:
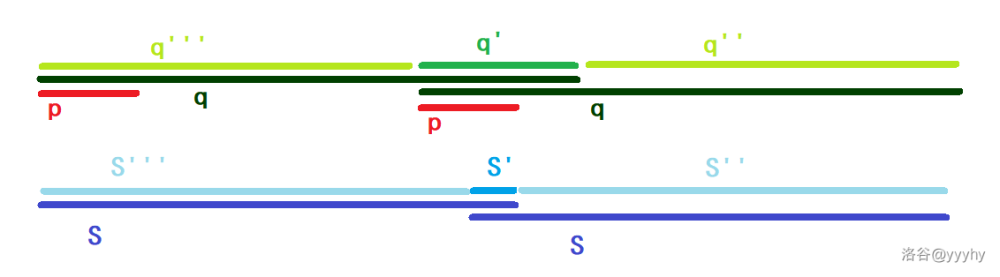
于是我们发现 $p$ 既为 $s$ 前缀,又为 $s$ 后缀,且长于 $s'$,这与假设矛盾,不成立。
所以 $s$ 是 $t$ 最长的 border。
所以现在问题就变成了求 $s$ 的最长 border,即 $s'$。
## 三、解决问题
首先,我们会想到枚举,即从 $n-1$ 到 $0$ 枚举 $|s'|$,复杂度 $O(n^2)$,加特殊性质可以干到 57pts,数据加强前实际 100pts,当然,现在~~骗不过了~~。
然后我们想优化:
### 字符串哈希
据说这是这道题黄题的原因,但我太蒟了,不会。
终于学会 hash 了!——2024·11·16
### hash 做法(11·16补充)
其实这个比较好实现,就是算出长度为 $i$ 的前缀和后缀的 hash,从 $n-1$ 开始(因为不能 $s'=s$)枚举到 $1$,有 hash 相等就记录跳出,最后输出。
但是众所周知,hash 非常好卡,所以为了保险我们用双 hash。
但是众所周知,双 hash 也能卡,所以为了追求 $100\%$ 正确率,最好加一层判断,从大到小判断每一对双 hash 都相等的前后缀是否真的一样,一样就跳出循环,也就是写一个无错双 hash。
~~这都卡那我就 T 罢(悲~~
于是取两个比较大的质数 $mod_1$ 和 $mod_2$,也就是代码中的 $m_1$ 和 $m_2$,进行 hash 操作,我取了 $10000003$ 和 $10000007$,因为有乘法,所以要开 `long long`。
hash 的计算比较简单就不介绍了,看代码应该看得懂。
其中:
$hash_1[0][i]$ 指 $\bmod m_1$ 情况下的前 $i$ 位 hash,
$hash_1[1][i]$ 指 $\bmod m_1$ 情况下的后 $i$ 位 hash,
$hash_2[0][i]$ 指 $\bmod m_2$ 情况下的前 $i$ 位 hash,
$hash_2[1][i]$ 指 $\bmod m_2$ 情况下的后 $i$ 位 hash。
[hash 代码](https://www.luogu.com.cn/paste/ybei2866),复杂度极大概率是 $O(n)$,卡死(应该做不到)$O(n^2)$。
这个比 SA 快多了,最慢 32ms。
### KMP/AC 自动机
没学过,也不会。(wtcl/kk)
想找这些做法请移步**其他题解**
#
于是我开始尝试用考场的第一反应:
### SA(后缀数组)
[板子在这里](https://www.luogu.com.cn/problem/P3809)
这玩意我就不多介绍了,板子题解里讲的非常详细。
但是板子题的题解也说了,光求后缀数组一般是没用的,还要求一个东西,就是每个**后缀**和后缀数组中**排序相邻的后缀**的**最大公共前缀长**。
先求再说:
```cpp
for (int i = 1, h = 0; i <= n; i++) {
if (h) h--;
int j = sa[rk[i] + 1];
while (i + h <= n && s[i + h] == s[j + h]) h++;
sam[rk[i]] = h;
}
```
解释一下:
定义 $sam[i]$ 为 $sa[i]$ 开始的后缀与 $sa[i+1]$ 开始的后缀的最大公共前缀长。
本来每两个后缀数组中相邻的后缀分别枚举会到 $O(n^2)$,但有一个特殊性质可以帮我们优化复杂度:
假设 $sam[sa[rk[i]]]=h$,那么 $sam[sa[rk[i+1]]]\geq h-1$。
reason:假设 $i$ 开始的后缀和 $j$ 开始的后缀最大公共前缀长为 $h>0$,那么 $i+1$ 开始的和 $j+1$ 开始的最大公共前缀长至少为 $h-1$,故 $sam[sa[rk[i+1]]]\geq h-1$。
这样由于 $h$ 不能超过 $n$ 且最多被减 $n-1$ 次 $1$。
所以复杂度 $\Theta(3n)$,不会 T。
那么我们知道了这个有什么用呢?
我们就可以求所有后缀中最长的,且满足是 $s$ 前缀的后缀了。
**接下来的思路:**
在 $sa[i]$ 中从 $rk[1]-1$ 倒序枚举到 $1$,分别看每个后缀和 $s$ 最大公共前缀长是不是等于从这个位置开始的后缀长,等于则记录跳出,这个最大公共前缀长即为 $|s'|$。
因为最大公共前缀长只减不增,所以最先枚举到的就是最长的。
**一个说明**:为什么向前枚举就行了?
因为 $s'$ 是 $s$ 的前缀,根据后缀数组的排序,$s'$ 作为后缀时的排序位置一定在 $s$ 位置的前面。
代码如下:
```cpp
int minl = inf, maxl = 0, nowwh = rk[1] - 1;
while (nowwh) {
minl = std :: min(minl, sam[nowwh]);
if (minl == n - sa[nowwh] + 1) {
maxl = minl;
break;
}
nowwh--;
}
```
最后输出即可。
[完整代码在这里](https://www.luogu.com.cn/paste/w6x96gey),复杂度 $O(n\log n)$,~~虽然做出来了但是好慢~~,最慢要 712ms。