写在前面

由于作者是一个初一蒟蒻，有一些地方可能存在问题，请多指教。喷轻点
感谢@biiwx123 大佬指出\text{Part\ 2}求e^x标程的错误
感谢@Thinking 大佬指出\text{Part\ 3} f'的错误
你以为我会先讲牛迭吗？
不可能！

先说说牛顿迭代法他爸的创始人——Newton

艾萨克·牛顿（1643年1月4日—1727年3月31日）爵士，英国皇家学会会长，英国著名的物理学家，百科全书式的“全才”，著有《自然哲学的数学原理》、《光学》。

他在1687年发表的论文《自然定律》里，对万有引力和三大运动定律进行了描述。这些描述奠定了此后三个世纪里物理世界的科学观点，并成为了现代工程学的基础。
他通过论证开普勒行星运动定律与他的引力理论间的一致性，展示了地面物体与天体的运动都遵循着相同的自然定律；为太阳中心说提供了强有力的理论支持，并推动了科学革命。

在力学上，牛顿阐明了动量和角动量守恒的原理，提出牛顿运动定律。

在光学上，他发明了反射望远镜，并基于对三棱镜将白光发散成可见光谱的观察，发展出了颜色理论。他还系统地表述了冷却定律，并研究了音速。

在数学上，牛顿与戈特弗里德·威廉·莱布尼茨分享了发展出微积分学的荣誉。他也证明了广义二项式定理，提出了“牛顿法”以趋近函数的零点，并为幂级数的研究做出了贡献。

在经济学上，牛顿提出金本位制度。

                                         ——摘自百度百科

注意这句话：

他也证明了广义二项式定理，提出了“牛顿法”以趋近函数的零点，并为幂级数的研究做出了贡献。

这里的“牛顿法”就是今天要讲的牛顿迭代法啦！

牛顿迭代法的故事

很久很久以前，次数高于四次方程不存在求根公式……

关于这个问题，大佬伽罗瓦用群论证明了。

因此求精确根非常困难，甚至不可能，从而寻找方程的近似根就显得特别重要。前面几项来寻找方程的根。
牛顿迭代法是求方程根的重要方法之一，其最大优点是在方程的单根附近具有平方收敛，而且该法还可以用来求方程的重根、复根，此时线性收敛，但是可通过一些方法变成超线性收敛。另外该方法广泛用于计算机编程中。

一位大佬——牛顿横空出世，他想到一个神奇的东西 —— 泰勒公式。

f(x)=\lim_{n\to \infty}\sum_{i=0}^{n}\frac{f^{(n)}(x_0)}{i!}(x-x_0)^i+R_n(x) 可是，$n\to\infty$，难道我们要$\Theta(\infty)$？~~那牛顿迭代法有什么用？~~ $$\large\color{red}\text{在\ OI\ 中，一般\ }n=10\text{\ 够了}$$ 但也不排除一些很坑的函数，这种另当别论。~~看造化~~ # 前置芝士 ## ~~0.加 减 乘 除~~ ## 1.函数 出门左转[函数 —— 百度百科](https://baike.baidu.com/item/%E5%87%BD%E6%95%B0/301912?fr=aladdin)、[人教版八下第十九章 一次函数](http://www.shuxue9.com/pep/cz8x/ebook/77.html)、[人教版高中必修 1 第一章 集合与函数概念](http://www.shuxue9.com/pep/gzbixiu1/ebook/12.html) 简单来讲，两个量 $x,y$ 如果有一种对应关系 $f$，那么这种对应关系 $f$ 就是自变量 $x$ 的函数 $f(x)$。 ## 2.导数 出门右转[导数 —— 百度百科](https://baike.baidu.com/item/%E5%AF%BC%E6%95%B0/579188?fr=aladdin)、[人教版高中选修 2-2 第一章 导数及其应用](http://www.shuxue9.com/pep/gzxuanxiu22/ebook/11.html) $$f'(x)=\lim_{\Delta x\to0}\frac{\Delta y}{\Delta x}=\lim_{\Delta x\to0}\frac{f(x+\Delta x)-f(x)}{\Delta x}$$ 简单来讲，在直线运动场景中，若 $x$ 表示时刻，$y$ 表示距离，函数 $f$ 表示时间与距离的关系 $y=f(x)$,那么导数 $f'(x)$ 的含义就是在第 $x$ 时刻的瞬时速度。 从某种意义上说导数的本质是一种极限，当自变量的增量无限接近 $0$ 时函数的增量与自变量的增量的比值。 从几何来看，导数是函数图像在 $(x,f(x))$ 处切线的斜率。 # $\text{Part\ 1}$ 理论知识 ## 1.线性逼近！ 先说一个关键问题：切线是曲线的线性逼近。 这个是什么意思呢？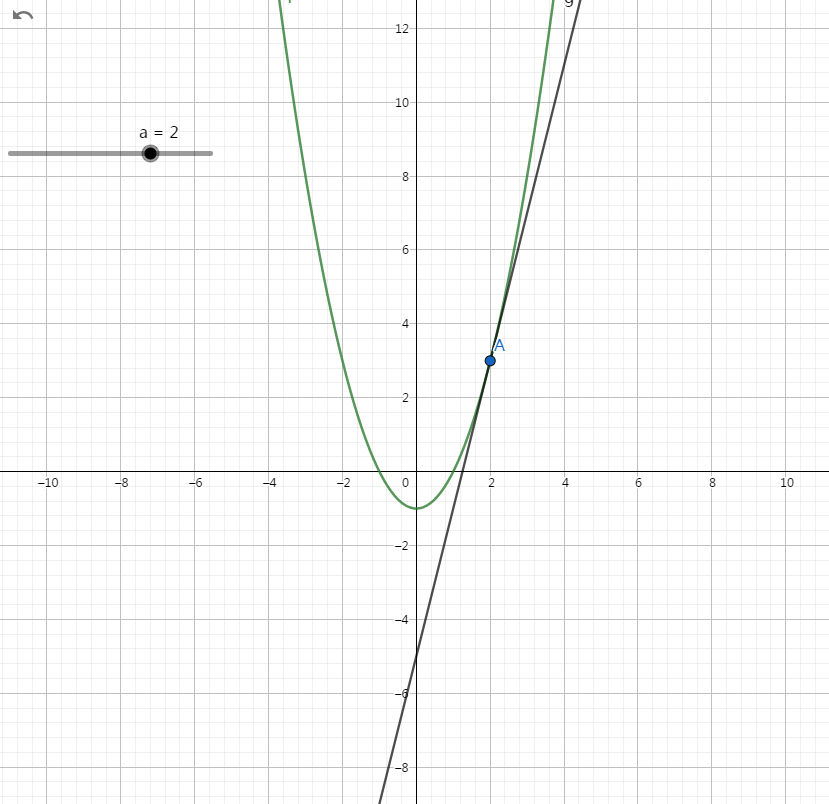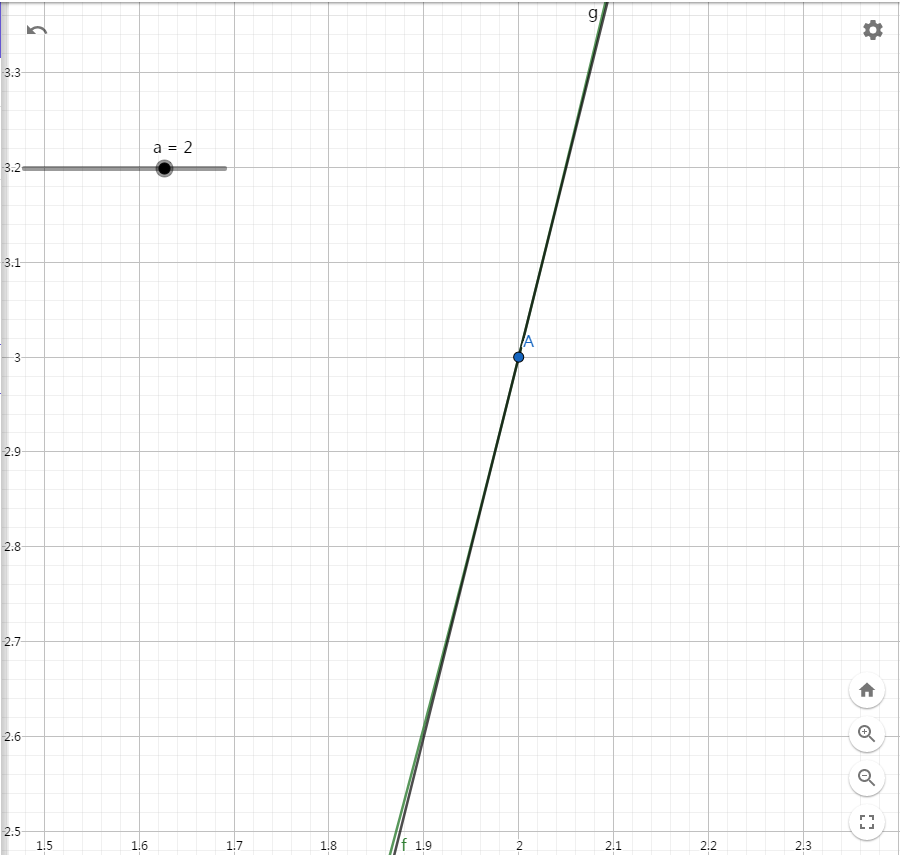我们来看一看，下面是 $f(x)=x^2-1$ 的图像： 我们随便选一点 $f(x)$ 上的一点 $A(a,f(a))$ 做它的切线：  我们在 $A$ 点处放大图像：  上图中，绿色的线是 $f(x)$，黑色的是 $A$ 点处的切线，可以看出放大之后切线和 $f(x)$ 非常接近了。很明显，如果我们进一步放大图像，$A$ 点切线就越接近 $f(x)$。 可以自己动手试试： $\text{Created\ with}$ [$\text{GeoGebra}$](https://www.geogebra.org/graphing/jjhfz6ca) 因为切线是一条直线，所以我们可以说，$A$ 点的切线 $g$ 是 $f(x)$ 的线性逼近。离 $A$ 点距离越近，这种逼近的效果也就越好，也就是说，切线与曲线之间的误差越小。所以我们可以说在 $A$ 点附近，“切线 $g\approx f(x)$”。 ## 2.牛顿迭代？ 设 $r$ 是 $f(x)$ 的根。 我们先~~随便~~选取 $x_0$ 作为 $r$ 的初始近似值，过点 $(x_0,f(x_0))$ 做切线，则与 $x$ 轴交点的横坐标 $x_1$，称 $r$ 的一次近似值。过点 $(x_1,f(x_1))$ 做切线，并求该切线与 $x$ 轴交点的横坐标 $x_2$，称为 $r$ 的二次近似值…… 搞个十次八次以后得到 $x_n$，**正常**情况下 $x_n\approx r$ 了…… 所以呢？没了？ ~~不可能~~你教我 C++ 怎么做切线？ 当然要转化为**代数式**了！ 怎么转？ 切线、导数、切线、导数、切数、导线…… 你发现什么了吗？ ~~切数和导线~~切线和导数好像是同一个东西啊…… ## 3.牛顿迭代公式！ 为了转化为代数式，我们可以先从特殊的情况入手。 设 $f(x)=x^2-1$，则 $f'(x)=2x$。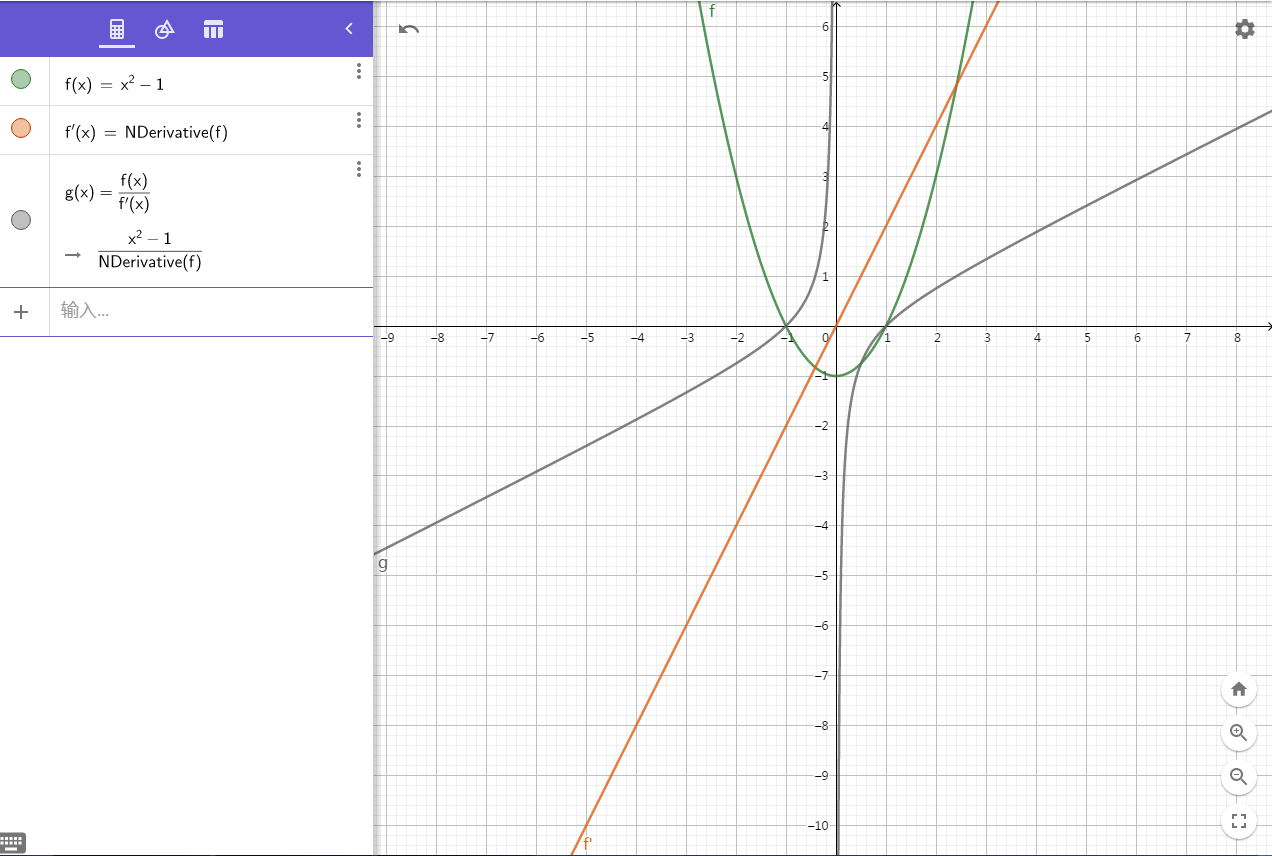 绘制一下函数图像：  体验一下？ $\text{Created\ with}$ [$\text{GeoGebra}$](https://www.geogebra.org/graphing/bezdqery) ~~显然~~，$x_n$ 点的**切线方程**为：$f(x_n)+f'(x_n)(x-x_n)$。 要求 $x_{n+1}$，即相当于求 $f(x_n)+f'(x_n)(x-x_n)=0$ 的根。 ？？？ 一个方程 $\implies$ 两个方程？？ 不不不。 $$f(x_n)+f'(x_n)(x_{n+1}-x_n)=0\implies x_{n+1}=x_{n}-{\frac {f(x_{n})}{f'(x_{n})}}$$ 我们发现了**递推公式**！ $$\large\color{red}x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}$$ ### 太神奇了！ ## 几何意义 设 $r$ 是 $f(x)$ 的根。 我们先选取 $x_0$ 作为 $r$ 的初始近似值，过点 $(x_0,f(x_0))$ 做切线，则与 $x$ 轴交点的横坐标 $x_1$，过点 $(x_1,f(x_1))$ 做切线，并求该切线与 $x$ 轴交点的横坐标 $x_2$…… 体验一下应该会理解的更加透彻。 $\text{Created\ with}$ [$\text{GeoGebra}$](https://www.geogebra.org/graphing/s7ddnkmg) 再送上维基百科动图： ## 另一个方向 回想一下泰勒展开： $$f(x)=\lim_{n\to \infty}\sum_{i=0}^{n}\frac{f^{(n)}(x_0)}{i!}(x-x_0)^i+R_n(x)$$ 我们取 $f(x)$ 的一阶泰勒展开（线性近似） $\phi(x)=f(x_0)+f'(x_0)(x-x_0)$。 我们用 $\phi(x)$ 替代 $f(x)$，那么问题转化为解 $\phi(x)=0$，即 $$f(x_0)+f'(x_0)(x-x_0)=0$$ 可化为 $$x=x_0-\frac{f(x_0)}{f'(x_0)}$$ 推广一下 $$x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}$$ ## 模板 ```cpp inline double Newton_find_root(function f/*原函数*/) { const unsigned n(20);//迭代次数 double x0(x); for (register unsigned i(1);i<=n;++i) x0-=f(x0)/f_derivative(x0); return x0; } inline double Newton_find_root2(function f/*原函数*/) { double x0; while (abs(f(x0))>eps) x0-=f(x0)/f_derivative(x0); return x0; } ``` 因为牛顿迭代法是平方收敛的，最坏情况 $\Theta(\log_2 n)$。 ## 适用性和弊端 它可以用来求方程的**一个根**，只要是可导函数都可以。 但是如果有多个根，就可能解出不符合题意的根，对初始值的依赖性强。 有很多坑（后面会讲）。 不过它也可以用来求极值，但是要保证有二阶导数（后面会也讲）。 # $\text{Part\ 2}$ 牛迭实战 ## 1.开平方 ### 给你一个正数$x$，让你用牛顿迭代法求 $\sqrt{x}$。 $$$$ $$$$ ### 解答 ```cpp inline double sqrt(double x) { double x0(x*0.5); while (abs(x0*x0-x)>1e-7) x0-=(x0*x0-x)/(2*x0); return x0; } ``` ### 很简单吧，下面有点难了 ## 2.$\exp

给你一个数 x，让你用牛顿迭代法求 \text e^{x}。

解答

inline double exp(double x)
{
    double x0(e*x);
    while (abs(log(x0)-x)>1e-7) x0-=(log(x0)-x)*x0;
    return x0;
}

\text{Part\ 3} 牛迭思考

1.精确估值

牛顿迭代法的初始估值越精确，速度越快。显然
那么精确估值显得十分重要了
那么 \text{How\ to} 精确估值?
这是一个值得思考的问题。

显然函数不同，估值也不同。
来个最简单的，f(x)=x^n-a,f'(x)=nx^{n-1}。
经过我的发现，x_0=\frac{a}{n}是最接近根点的。
至于其他的，读者自己思考。明明就是你懒得想

2.求值

在\text{Part\ 2}中，我们知道了牛顿迭代法可以用来求值，那请问 f(a)=???
经过我的观察发现，要求 f(a)，其实就可以通过寻找 g(x)=f^{-1}(x)-a 的根，就是 f(a)。
显然，g'(x)=(f^{-1}(x))'。
设 y=f^{-1}(x),f(y)=x，
则 f'(y)=x'=1，所以 \frac{df(y)}{dy}\cdot\frac{dy}{dx}=1，所以 (f^{-1}(x))'=(f'(y))^{-1}

3.bug???

3.1.驻点???

起始点不幸选择了驻点，从几何上看切线 \parallel x 轴，根本没有根。 从代数上看，x_{n+1}=x_{n}-{\frac {f(x_{n})}{f'(x_{n})}} 没有意义（f'(x_{n})=0）。

3.2.不收敛???

下面是 f(x)=\sqrt[3]{x}：

我们发现不论怎么选择起始点，越迭代就越远离根点。

从代数上看

x_{n+1}=x_n-\frac {f(x_n)}{f'(x_n)}=x_n-\frac{\sqrt[3]{x_n}}{\frac{1}{3}x^{-\frac{2}{3}}}=-2x_n

就是说下一个点比上一个点更远离根点。
此处根显然是0，但是f'(0)=0，无法迭代。
天理不容啊！！！

3.3.循环震荡???

还有一种更酸爽的不收敛，就是不断的循环震荡。 比如下面是 f(x)=\sqrt{|x|} 的曲线：

从代数上看

x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}=x_n-2x_n=-x_n

由于选择的起始点不对，造成这种循环的情况其实还挺多，在很多曲线的某些点都会出现这种情况。

3.4.\text{无法迭代???}

有一天，%%%LCX 大佬突发奇想，想用牛顿迭代法求平方，他的思路是这样的：

a^2\implies\text{解}\ \sqrt{x}-a=0 \text{设}\ f(x)=\sqrt{x}-a,f'(x)=\frac{1}{2\sqrt{x}} x_{n+1}=x_n-\frac{\sqrt{x_n}-a}{\frac{1}{2\sqrt{x_n}}}=x_n-2\sqrt{x_n}(\sqrt{x_n}-a)=x_n-2x_n+2a\sqrt{x_n}=2a\sqrt{x_n}-x_n

他兴高采烈地打出了程序，然而……

\Large\color{red}\text{炸了！！！}

他叫我过去帮他检查一下，发现出现了负数开平方或0的情况……

\text{Why???}

下面是f(x)=\sqrt{x}-2的曲线：
一般情况是这样的 (0<x_0<16)：

二般情况是这样的（负数开平方）(x_0>16)：

三般情况是这样的(0 发生了循环 ,x_0=16)：

感受一下？

由于选择的起始点不对，造成这种情况其实还挺多…… ~~不过求算数平方根可没这么坑。~~ ~~ZXJ：“LCX 叫你作死，叫你作死，傻了吧哈哈哈哈哈哈哈……”~~ # $\text{Part\ 4}$ 应用于最优化问题 牛顿法也被用于求函数的极值。 因为导数的物理定义是物体的瞬时速度，所以函数极值点处的导数值为零。 因此导函数的零点就是原函数的极值点。 因此我们要求原函数的极值点，我们可以使用牛顿迭代法找到导函数的零点。 递推式如下： $$\large\color{red}x_{n+1}=x_n-\frac{f'(x_n)}{f''(x_n)}$$ # $\text{Part\ 5}$ 推广 刚才我们学习了牛顿迭代法，不过这只是一元函数，对于多元函数$f(x)$，我们只需要将一元函数牛顿迭代法中的 $f'(x)$ 改为 $\nabla f=\{\frac{\partial f}{\partial x_1},\frac{\partial f}{\partial x_2},\cdots,\frac{\partial f}{\partial x_n}\}$，就是梯度，是一个向量，所以结果也是向量。 在高维下，$\phi(x)=f(x_0)+\nabla f(x_0)^T(x-x_0)$。 解 $\phi(x)=0$。 递推公式为： $$x_{n+1}=x_n-f(x_n)\nabla f(x_n)^T$$ 不过这计算很慢，优化的方法有 DFP，BFGS，Broyden 等。 # $\text{Part\ 6}$ 小结 既然你看到了这里，一般来说牛顿迭代法你已经 get 到了。 其实核心就是一个式子： $$\Large\color{red}x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}$$ 非常简洁。 ~~如果你累了，可以退出。~~ 还有其实牛顿迭代法在 $\text{OI}$ 中的主要应用还是解方程，求解多项式问题，极值问题等。 $$\Large\color{purple}\text{牛顿迭代法完结撒花！！！}$$ $$$$ $$$$ $$$$ $$$$ $$$$ # 新的思考？ 有一些~~变态的~~函数，$f(x)$ 十分简单，但是 $f'(x)$，不易算出，或是过于复杂。~~不符合毒瘤出题人的审美~~ 比如：……~~（作者找不到栗子……）~~ 为了避免计算麻烦的 $f'(x)$，自然有大佬改变方法…… # 割线法！！！ **割线法的基本思想是用*弦的斜率*近似代替*切线斜率*，并用割线与横轴交点的横坐标作为方程式的根的近似。** ## 具体步骤 $f(x)$ 上~~随便~~找两点 $(x_n,f(x_n))$ 和 $(x_{n-1},f(x_{n-1}))$，两点所在的**直线**就是割线，~~显然~~直线方程为： $$y-f(x_n)=\frac{f(x_n)-f(x_{n-1})}{x_n-x_{n-1}}(x-x_n)$$ ？？？ 一个方程 $\implies$ 两个方程？？ 不不不。 $$y-f(x_n)=\frac{f(x_n)-f(x_{n-1})}{x_n-x_{n-1}}(x-x_n)\implies x=x_n+\frac{(y-f(x_n))(x_n-x_{n-1})}{f(x_n)-f(x_{n-1})}$$ 我们要求割线与横轴交点的横坐标，设为 $x_{n+1}$。 ~~显然~~ $x_{n+1}\approx x,y=0$。 $$\therefore \color{red}x_{n+1}=x_n-\frac{f(x_n)(x_n-x_{n-1})}{f(x_n)-f(x_{n-1})}$$ 据说它收敛更快？？？平方收敛？？？ $$\Large\color{purple}\text{割线法完结撒花！！！}$$ $$$$ $$$$ $$$$ $$$$ $$$$ # 题外话 —— 平方根倒数速算法（卡马克开方法） 这有悠久的历史…… 平方根倒数速算法是适用于快速计算平方根的倒数（符合 IEEE 754 标准格式的 32 位浮点数）的一种算法，于 1999 年在《雷神之锤 III 竞技场》的源代码中应用。 此算法首先接收一个**32 位带符浮点数**，然后将之作为一个**32 位整数**看待，以将其向右进行一次逻辑移位的方式将之**取半**，并用 `0x5f3759df` 减之，如此即可得首次近似值，以牛顿法反复迭代，以求出更精确的近似值。在计算浮点数的平方根倒数的同一精度的近似值时，此算法比直接使用浮点数除法要**快四倍**。 上源码： ```cpp float Q_rsqrt( float number ) { long i; float x2, y; const float threehalfs = 1.5F; x2 = number * 0.5F; y = number; i = * ( long * ) &y; // evil floating point bit level hacking i = 0x5f3759df - ( i >> 1 ); // what the fuck? y = * ( float * ) &i; y = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration // y = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration, this can be removed return y; } ``` 后来，$\text{Chris\ Lomont}$ 大佬站了出来，他找到了一个更加精确的数字`0x5f375a86`。 （相关资料[戳我](https://diducoder.com/sotry-about-sqrt.html)） 后来，又有大佬站了出来，他找到了 **64 位**的 IEEE754 浮点数（即**双精度类型**）所对应的魔术数字是 `0x5fe6eb50c7aa19f9`。 ## 原理??? ~~我也不知道……会用就行。~~ 可以参考这篇文章 —— [揭秘·变态的平方根倒数算法](https://segmentfault.com/a/1190000006170378) $$$$ $$$$ $$$$ $$$$ $$$$ $$\Huge\color{purple}\text{完结撒花！！！}$$ $$$$ $$$$ $$$$ $$$$ $$$$ # 参考资料 - [牛顿法_百度百科](https://baike.baidu.com/item/牛顿法/1384129?fr=aladdin) - [如何通俗易懂地讲解牛顿迭代法？——马同学高等数学](https://www.matongxue.com/madocs/205/) - [割线法_百度百科](https://baike.baidu.com/item/割线法/5806354?fr=aladdin) - [平方根倒数速算法_百度百科](https://baike.baidu.com/item/平方根倒数速算法/4075273?fr=aladdin) - [揭秘·变态的平方根倒数算法](https://segmentfault.com/a/1190000006170378) - [一个 sqrt 函数引发的血案](https://diducoder.com/sotry-about-sqrt.html) # 后记 感觉自己好菜啊…… 希望这篇文章对你有用。 在这之后，我还会写一下其他常用的最优化算法。 等着吧…… 还有，牛顿迭代法不是线性近似（一阶泰勒展开）吗？那我用二阶泰勒展开岂不是更好？