\text{stO lxl Orz}
您将在此看到 OIer 分块的最低水平。
0. 分块概论
在数据结构问题中,我们需要维护一些离散的信息单位,单位的数目会影响处理的复杂度。
如果信息支持不受限制的合并与批量处理,那么就可以使用线段树等区间数据结构。
当然,有时并不存在高效的信息合并化简方式,而需要在“批量”和“零散”之间找到平衡点,这就是分块的核心思想。
这一类问题的性质更弱,所以问题形式变化多端,“整散”关系多种多样,具有传统数据结构难以比拟的灵活性。
1. 基础数列分块
在这一节中,我们将认识一些经典的数列分块问题,初步熟悉分块的形式和思想。
下面统一约定数列长度为 n ,块大小为 B。
如图,在分块中有如下概念 :
-
末尾小块 : 因为整个数列划分不整而得到的一个较小的块,可能带来多余的细节。有时可以人为地增长数列将小块变成正常大小的块。
-
整块 : 被操作区间完整覆盖的块。总块数是 O(n/B) 的。
-
散块 : 被操作区间覆盖了一部分的块。散块包含的元素数目是 O(B) 的。
找出所有的 整块 和 散块内元素 是容易的。
在这个问题中,信息能够高效合并,这使得分块没有太大的优势。
但是,从这一类简单问题入门分块比较易于初学者理解。
-
区间查询 (一般先分析查询,搞清楚需要维护什么,再考虑如何维护)
注意到,每个元素对答案的贡献是独立的。我们可以对每个 块 / 散块 分别计算贡献。
(大多数分块都会满足这个性质,因为块间贡献一般很难考虑)
对每个整块记下总和,这样容易 O(1) 计算贡献。对于散块,暴力求和。
-
区间修改
对于散块,暴力加。
对于整块,记录加法标记。
这样,总和 = 块内元素总和 + 标记 \times 块大小。
当取单个元素时,要加上对应块的加法标记。
两者的复杂度均为 O(n/B+B) ,令 B=\sqrt{n} 得到最优复杂度 O(q\sqrt{n})。
思考我们这样做的本质,不难发现,其实是将线段树这一 “二叉树” 改成了 “\sqrt{n} 叉树” 。
上面的做法对应标记永久化,其实也可以将标记下推,即每次暴力清空两个散块的标记,复杂度不变。
评测记录 | 代码Link
-
**题意** : 区间加,查询区间大于等于 $k$ 的数的个数。
-
区间查询
这里贡献仍然独立。
考虑在每个块内维护有序序列,这样只需要一次二分即可计算块内贡献。
对于散块,暴力遍历即可。
若块大小为 B ,则复杂度为 O((n/B)\log B+B)。
-
区间加
对于整块,块内的相对顺序不变,只需记录加法标记。注意考虑加法标记对二分比较的影响。
对于散块,需要重构有序序列,若加完后暴力排序,复杂度是 O(B\log B)。
在旧的有序序列中提取加和未被加的两部分,各是有序序列,归并即可做到 O(B)。
复杂度 O((n/B)+B)。
令 B=\sqrt{n\log n} 得到最优复杂度 O(q\sqrt{n\log n})。
复杂度分析技巧 : 分块的主要思想是平衡,若复杂度由两部分组成,直接令两者相等,即可解得最优块大小。
(本题数据非常弱,错误做法可能可以通过)
类似上一题,对每个块维护有序序列,查询时整块二分,散块暴力。
复杂度 O(q\sqrt{n\log n})。
评测记录
对每个块维护有序序列,查询时二分转化成 P2801。复杂度为 O(q\sqrt{n\log n}\log w) ,无法通过。
仔细分析查询时的操作 : 整块二分,散块暴力。
根据信息论,整块二分难以优化。但对散块进行 O(\log w) 次暴力有些浪费。
可以事先将散块归并,这样对散块的查询无需暴力遍历,而可以一次二分搞定。
这样,单次询问的复杂度改进为 O\big((n/B)\log B\log w+B \big)。
若将 \log w 视为与 \log n 同阶,则 令 B=\sqrt{n}\log n 可得复杂度为 O(q\sqrt{n}\log n),卡常后可以通过。
注意,散块部分的常数较大,应适当调小块大小。
评测记录
附 : 觉得不过瘾可以做 P3380 【模板】二逼平衡树(树套树)
-
**题意** : 维护一个 $n$ 个点的有向图,每个点都有且仅有一条出边,且指向比自己编号大的点。
支持修改某个点的出边,查询从某个点出发几步会到达 $n$ 号点。
“行动步数”问题和经典的求算贡献问题有很大不同。
不难发现,若没有修改,容易 O(n) 求出各个点的答案。
对于一个块,预处理其每个元素走出该块所需步数,以及到达的点。
这样,可以 O(1) 跳过一个块。查询复杂度改进为 O(n/B+B)。
在修改时,也只需 O(B) 重构一个块。
令 B=\sqrt{n} 可得复杂度为 O(q\sqrt{n})。
评测记录
-
**题意** : 给定两个长度为 $n$ 的数列 $A,B$ ,支持下列操作:
- 将数列 $A$ 中区间 $[l,r]$ 内所有数加上 $w$ ;
- 交换 $B_x$ 和 $B_y$ ;
- 求 $\max\limits_{i\in[l,r]}\{A_i\times B_i\}$ .
操作二可以直接把涉及到的两个块重构。
区间加时,散块可以暴力重构,但是整块只能打标记。
每个位置的贡献可以看做关于标记的一次函数,于是维护凸壳即可。
散块重构时利用归并可以 O(B) 建立凸壳。
查询时,由于标记只会递增,线性扫即可。
令 B=\sqrt{n} 可得复杂度为 O(q\sqrt{n})。
-
**题意** : 查询区间内出现偶数次的数(称为好数)的个数,强制在线。值域在 $O(n)$ 级别。
此时贡献是不独立的,对每个块分别考虑并不方便。
利用桶记录每个数的出现次数(奇偶性),即可增量维护好数的个数。
记 s[i,j] 为块 [i...j] 中好数个数,可以 O(n/B) 次从各个块开始增量维护得到,复杂度为 O(n^2/B)。
记 o[i][x] 表示前 i 个块中 x 的出现次数(奇偶性),通过差分,可以得到任意块区间中某个数的出现次数。
查询时,若 [l,r] 包含的整块区间为 [L,R] ,则先取出 s[L,R]。
然后考虑散块的影响,仍然用增量法计算即可。
总复杂度为 O(nB+n^2/B) ,令 B\sqrt{n} 可得复杂度为 O\big((n+q)\sqrt{n}\big)。
若要节省空间,可以用 bitset 记录 o ,则空间可以做到 O(n\sqrt{n}/w)。
可以发现,本题思想类似于回滚莫队。实际上,静态分块的功能是莫队的子集,所以强制在线时分块才有优越性。
基本操作和上一题非常类似。
贡献不独立。
用桶记录每个数的出现次数(奇偶性),即可增量维护众数。
记 s[i,j] 为块 [i...j] 中的众数,利用增量求解。
记 o[i][x] 表示前 i 个块中 x 的出现次数。
查询时,若 [l,r] 包含的整块区间为 [L,R] ,则先取出 s[L,R]。
然后考虑散块的影响,仍然用增量法计算即可。(注意散块对出现次数也有贡献)
时空复杂度均为 O(n\sqrt{n})。
-
**题意** : 区间众数,强制在线。要求空间 $O(n)$。
在上一题中,空间的瓶颈是 o 数组。观察其用途 : 判定散块中某个数在询问区间中的出现次数是否 >k。
我们可以用 vector 记录下同类数的所有出现位置。
当判定散块中数 u 出现次数是否 >k 时,假设 u 是询问区间内同类数的最靠左出现(左侧散块,右侧散块类似),则检查 u 后面的第 k 个同类数是否在询问区间外即可。
空间复杂度改进为 O(n) ,时间常数也减小了。
在逆序对问题中,每一对数都有贡献,贡献模式是二维的。
询问时,答案的贡献成分如下图 :
绿色是整块内部的贡献,橙色是散块内部的贡献,红色是整块和散块之间的贡献,蓝色是散块之间的贡献。
考虑对每个块内前后缀都预处理内部逆序对数,容易使用树状数组做到 O(n\log n),这样就解决了橙色部分。
考虑归并排序的过程,不难两个区间之间的逆序对可以将这两个区间归并计算。
于是,预处理块内有序序列,蓝色部分就可以(先取出有序散块)归并计算。
然后预处理 s[i,j] 表示块 i...j 内部的逆序对数。
考虑差分,有 s[i,j]=s[i+1,j]+s[i,j-1]-s[i+1,j-1]+(\text{块}i,j\text{之间的贡献})
两块间贡献仍然可以 O(\sqrt{n}) 归并计算,则预处理复杂度为 O(n\sqrt{n})。绿色部分完成。
接下来预处理 o[i][x] 表示前 i 个块中 \leq x 的数的个数,然后可以计算红色部分(对每个散块元素分别统计贡献)。
复杂度为 O(n\sqrt{n})。此做法常数较大。
还有另一个常数较小的做法,预处理 f[i][j] 表示 [1...i] 中的数与第 j 个块之间的贡献,利用桶(值域前缀和)不难做到 O(n\sqrt{n})。
这样,计算两块之间的贡献时,直接差分即可(不需要常数巨大的归并)。
计算红色部分时,可以转而枚举整块,然后差分。
蓝色部分依然需要归并计算。
2. 经典分块技巧
一些 基于分块的技巧 和 分块需要的技巧。
某些分块可以视作三层的 \sqrt{n} 叉树,如图。
块状数组查询和修改的复杂度一优一劣,用于查询和修改数目不同的问题,以平衡复杂度。
-
维护块和,修改时只需修改对应元素以及块和,查询时和数列分快相同。
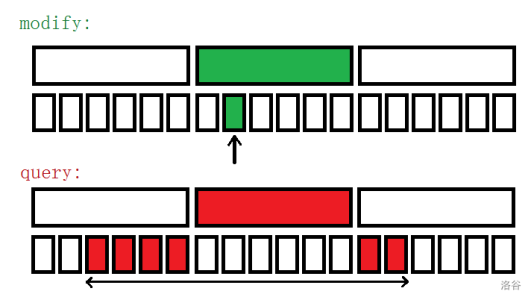
-
维护块内前缀和,块和的前缀和。查询时整块正缀和加上块内前缀和。
修改时暴力 $O(\sqrt{n})$ 分别重新计算块内前缀和和块和的前缀和。
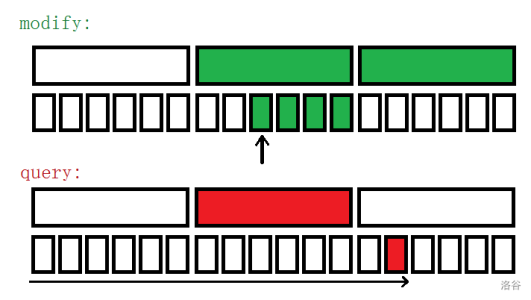
当值域大小为 O(n) 时,可以用类似权值线段树的形式维护 “权值 \sqrt{n} 叉树”。这个技巧被称为值域分块。
将区间分块。维护 c[k][i] 表示在第 k 块中第 i 个位置被覆盖了多少次。
这样,在单点修改之后,能 O(\sqrt{n}) 地计算出各个块的和的变化。
查询时,对于散块暴力 O(\sqrt{n}) 次区间求和,使用 O(\sqrt{n}) 修改 O(1) 求和的分块即可。
将上述三层 \sqrt{n} 叉树可持久化即可。可以搞出“块状主席树”之类的东西。
例题 : P5574 [CmdOI2019]任务分配问题 ( O(n\sqrt{n}+nk\log n) )
解决一系列带插入的序列问题。(在带插入的序列上维护分块)
将某个元素插入某个块时,将该块重构。若某个块的大小超过 2B (或其他自定常数)则分裂为两个大小为 B 的块。
这样,分裂次数是 O(n/B) 的,且能保证各个块的大小在 [B,2B] 之间。
代码实现细节较多,具体见例题。
在远古时期这题的时限是 \texttt{1s} ,故几乎只有实现较好的分块能通过。
先考虑带单点修改区间K小值,若沿袭 P5356 的做法,复杂度为 O(q\sqrt{n}\log n) ,无法接受。
注意到本题的特殊性 : 值域较小(认为与 n 同阶)。这启发我们使用值域分块。
维护序列块的前缀权值块状数组,差分能得到任意一端块的权值块状数组。再将散块 O(B) 建立一个权值块状数组。
在线性组合后的权值块状数组上,模仿主席树二分来爬,复杂度是 O(\sqrt{n}) 的。
在单点修改时,只会有 O(n/B) 次 O(1) 的权值块状数组更新。
取 B=\sqrt{n} 即可做到 O(n\sqrt{n})。
接下来考虑插入,只需多考虑分裂操作。
评测记录 | 代码Link
题意 : 维护一个序列,支持(在指定元素后面)插入元素,询问两个元素的先后顺序。
显然可以使用平衡树维护,回答询问时,求出两者的排名并比较。这样能做到 O(\log n) 修改 O(\log n) 查询。
考虑给每个元素一个标号,是的先后顺序和标号的大小顺序相对应。
给根一个值域区间,如 [0,1] 或 [0,2^{60}-1],将点 u 的权值设为自己区间的中点 mid=(u.l+u.r)/2,并令左右儿子的值域区间分别为 [u.l,mid],[mid,u.r]。
显然,这样得到的权值也满足左小右大的性质。若平衡树的最大高度为 h ,则权值精度要求是 O(2^h) 的。
使用重量平衡树(如替罪羊树)来维护这个序列,这样能够保证我们每次操作更新(并重新标记权值)的子树大小是 O(\log n) 级别的。
而且,替罪羊树的树高严格 \leq \log_{1/\alpha} n (一般不超过 3\log n),故对精度的要求也较低(低于 O(n^3)),使用 double 或 long long 即可满足。
比较先后顺序时,只需比较标号即可,这样即可做到(均摊) O(\log n) 修改 O(1) 查询。
将序列分成块状链表的形式,每一块的大小在 [\log n,2\log n] 之间,适时分裂。
块外用替罪羊树维护。共产生 O(n/\log n) 次分裂,故复杂度为 O(n)。
比较时,先比较所在块的先后顺序,再比较块内的先后顺序。
块内使用链表维护,插入的元素的权值设置为前驱和后继权值的平均数,这样所需的值域也并不大。
-
严格 O(1) : 先咕咕。
-
**题意** : 静态序列,查询区间 $\min$。
该问题的一个经典做法是 \rm ST 表,但需要 O(n\log n) 的预处理时间。
考虑将原序列分为 O(\log n) 一块,每一块预处理前/后缀 \min ,整块的 \min 上建立 \rm ST 表。
这样,若查询的区间端点异块,则使用散块前/后缀 \min 拼上一段整块的 \min 就能做到 O(1) 查询。
上面的复杂度是 O(n)-O(1) 的。
若区间端点同块,只能暴力,但是题目中一般不会出现这种情况。这样,我们就得到了一个简易的 O(n)-O(1)\ \rm rmq 替代品。
递归套用本算法可以得到 O(n\alpha (n))-O(\alpha (n)) 的做法,但不实用。
3. 根号分治 & 自然根号
有时,根号复杂度会产生于一些非常自然的问题中。
例 : 有若干数和为 n ,则最多有 n/a 个数字大于 a。
若对于某个数可以 O(x) 处理,那我们就以 O(xa) 的复杂度保证了其余数都 \leq a。
点度数总和是 O(m) 的,对度数进行根号分治。
对于度数 \geq \sqrt{m} 的点,称为大点,反之称为小点。
在查询小点时暴力。修改时主动给周围的大点贡献,由于大点数目是 O(\sqrt{m}) 的,一次修改也不会超过 O(\sqrt{m})。
总复杂度 O(q\sqrt{m})。
考虑 x\geq \sqrt{n} 的询问,显然可以 O(\sqrt{n}) 计算。
对于剩下每个询问 (x,y) ,都维护其答案。在单点修改时,对于每个 x 都有一个 y 的答案改变,复杂度也是 O(\sqrt{n})。
-
练习题
-
[DS记录]P5309 [Ynoi2011]初始化
-
[DS记录]P5528 [Ynoi2012]WC,THUWC,CTSC与APIO2017
-
[DS记录]P5397 [Ynoi2018]天降之物
-
[??记录]CF1039D You Are Given a Tree
-
题解 CF1039E 【Summer Oenothera Exhibition】
-
有若干数和为 $n$ ,则最多有 $O(\sqrt{n})$ 个不同的数。
显然,最差情况是 n=1+2+3+...+m ,和是 O(m^2) 级别的,故 m=O(\sqrt{n})。
-
有 $m$ 个集合,大小分别为 $S_1,S_2...S_m$。设 $n=\sum_{i=1}^mS_i$。
有 $q$ 次对子询问,处理询问 $(x,y)$ 的复杂度为 $O\big(\min(S_x,S_y)\big)$。
若将询问记忆化,则总复杂度为 $O(n\sqrt{q})$。
证明 : 我们选出复杂度最大的 q 个不同的询问进行求和。
记 S 从大到小排序后的结果为 S' ,复杂度最大的 q 个不同的询问的复杂度和为 O\Big(\sum_{i=1}^{\sqrt{q}}S_i\times i\Big)。
最差情况是 S 为 O(\sqrt{q}) 个 O(n/\sqrt{q}) ,此时复杂度为 O(n\sqrt{q})。
例题 : P5576 [CmdOI2019]口头禅
-
对于(多串建立的)广义 SAM ,定义节点 $u$ 的 $siz_u$ 为 $parent$ 树子树内串的种类数。
(即将输入中第 $i$ 个串的所有终止节点加上标记 $i$ ,问子树内不同标记个数)
设 $n=\sum_i|S_i|$ ,则 $\sum_u siz_u$ 是 $O(n\sqrt{n})$ 级别的。
证明 : 对于某个 S_i ,其贡献的复杂度显然为 O\big(\min(|S_i|^2,n)\big)。
当 |S_i|>\sqrt{n} 时,这样的串只有 O(\sqrt{n}) 个,就算跑满 O(n) 的复杂度,也仅为 O(n\sqrt{n})。
当 |S_i|\leq \sqrt{n} 时,复杂度不超过 O(\sum |S_i|^2)\leq O(n*\max|S_i|)=O(n\sqrt{n})。
也存在达到此上界的构造,可见 Itst : 广义 SAM 上每个模板串包含的节点数量和的上界以及构造
例题 : [Str记录]CF204E Little Elephant and Strings
-
将 $\rm SAM$ 上每个节点的 $\rm endpos$ 集合划分为若干等差序列。等差序列的总个数为 $O(n\sqrt{n})$。
证明 :
-
-
由此,只有 $>len/2$ 的空位才能隔断某个等差数列,故每个点的等差数列个数至多是 $O(n/len)\leq O(\sqrt{n})$ 的。
也存在达到此上界的构造,限于篇幅故不展示。
找出这些等差序列的方法暂不介绍,有题目之后再说。
-
一个串的 $\rm Border$ 可以被划分为若干等差序列,其中公差 $>B$ 的等差序列总大小 $\leq O(n/B)$。
$\rm Border$ 长度按照 $[2^0,2^1),[2^1,2^2),...[2^k,2^{k+1})...$ 分段后,可以证明每一段内至多只有一个等差序列。
故公差 $>B$ 的等差序列总大小是 $O(\sum_{k}(n/2^k)/B)=O(n/B)$。
例题 : [[Str记录]Loj#6681. yww 与树上的回文串](https://www.luogu.com.cn/blog/command-block/str-ji-lu-loj6681-yww-yu-shu-shang-di-hui-wen-chuan)
## 4. Ynoi 分块选做
题解都较为繁琐,故不在同一篇文章中展示。
- [[DS记录]P5063 [Ynoi2014] 置身天上之森](https://www.luogu.com.cn/blog/command-block/ds-ji-lu-p5063-ynoi2014-zhi-shen-tian-shang-zhi-sen)
- [[DS记录]P5611 [Ynoi2013]D2T2](https://www.luogu.com.cn/blog/command-block/ds-ji-lu-p5611-ynoi2013d2t2-post)
- [[DS记录]P5073 [Ynoi2015] 世上最幸福的女孩](https://www.luogu.com.cn/blog/command-block/ds-ji-lu-p5073-ynoi2015-shi-shang-zui-xing-fu-di-ru-hai)
- **最初分块** : [[DS记录]P4119 [Ynoi2018]未来日记](https://www.luogu.com.cn/blog/command-block/ds-ji-lu-p4119-ynoi2018-wei-lai-ri-ji)
- **第二分块** : [[DS记录]P4117 [Ynoi2018]五彩斑斓的世界](https://www.luogu.com.cn/blog/command-block/ds-ji-lu-p4117-ynoi2018-wu-cai-ban-lan-di-shi-jie) (大分块入门推荐)
- **第四分块** : [[DS记录]P5397 [Ynoi2018]天降之物](https://www.luogu.com.cn/problem/P5397)
- **第四分块·改** : [[DS记录]P5692 [MtOI2019]手牵手走向明天](https://www.luogu.com.cn/problem/P5692)
- **第六分块** : [[DS记录]P4118 [Ynoi2018] 末日时在做什么?有没有空?可以来拯救吗?](https://www.luogu.com.cn/problem/P4118)
- **第十分块** : [[DS记录]P6578 [Ynoi2019]魔法少女网站](https://www.luogu.com.cn/blog/command-block/ds-ji-lu-p6578-ynoi2019-mo-fa-shao-ru-wang-zhan)