浅谈数论分块

问题引入

求 \sum_{i=1}^n \lfloor\frac{n}{i}\rfloor，其中 n 为常数。

为了方便我们的研究，我使用绘图软件画出了 f(x) =\frac{7}{x}(1\leq x\leq 7) 的图像，也就是一种反比例函数的图像。

因为求的值是向下取整的，显然函数 f(x) 在 [1,7] 区间内是单调递减的，我们不妨把 \lfloor \frac n i\rfloor 取值相同的段取出来

图像被分割为了 7 个大块，但取值范围包含整数的只有 4 个，那么如果我们可以把这些包含整数的块取出来，一次性得出一个块的答案，把整块对答案的贡献加上即可。

实现：

如果要实现整块一起统计，我们需要求出每一块的块头 l 和块尾 r，则：

\sum_{i=1}^n \lfloor \frac n i \rfloor = \sum _{(l,r)} (r-l+1) \lfloor \frac n l \rfloor

给出一个结论： 对于整数 i，其所在块的右端点为 \lfloor\frac{n}{\lfloor \frac n i \rfloor}\rfloor，在此给出两种证明方式：

1. 代数法

首先我们要证明 \lfloor\frac{n}{\lfloor \frac n i \rfloor}\rfloor 与 i 在同一块，也就是：

\lfloor\frac{n}{\lfloor\frac{n}{\lfloor \frac n i \rfloor}\rfloor}\rfloor= \lfloor\frac{n}{i}\rfloor

易证：

\lfloor x\rfloor \leq x x \le y\to \lfloor x\rfloor \le \lfloor y\rfloor x \ge y\to \lfloor x\rfloor \ge \lfloor y\rfloor

则：

\lfloor\frac{n}{\lfloor\frac{n}{\lfloor \frac n i \rfloor}\rfloor}\rfloor \ge \lfloor\frac{n}{\frac{n}{\lfloor \frac n i \rfloor}}\rfloor=\lfloor\frac{n}{i}\rfloor \lfloor\frac{n}{\lfloor\frac{n}{\lfloor \frac n i \rfloor}\rfloor}\rfloor \le \lfloor\frac{n}{\lfloor\frac{n}{ \frac n i }\rfloor}\rfloor=\lfloor\frac{n}{i}\rfloor

所以：

\lfloor\frac{n}{\lfloor\frac{n}{\lfloor \frac n i \rfloor}\rfloor}\rfloor= \lfloor\frac{n}{i}\rfloor

我们还要证明：

i \le \lfloor\frac{n}{\lfloor \frac n i \rfloor}\rfloor

也就是 \lfloor\frac{n}{\lfloor \frac n i \rfloor}\rfloor 是这个块内最大的，即为块的右端点，这个很好证明：

\lfloor\frac{n}{\lfloor \frac n i \rfloor}\rfloor\ge \lfloor\frac{n}{ \frac n i }\rfloor=i

这样我们就以代数方式证明了结论，如果看不懂还有几何的。

2. 几何法

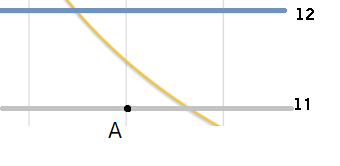[](https://imgtu.com/i/oi5Jne) $l_1$ 为直线 $y = \lfloor \frac n i \rfloor $，$l_2$ 为直线 $y=\lfloor \frac n i \rfloor +1$，我们不妨设 $l1$ 与直线 $y=\frac n x$ 的交点为 $P$，$l_2$ 与直线 $y=\frac n x$ 的交点为 $Q$，则： $$\forall x_{Q} < x \le x_{p}, \lfloor\frac n x\rfloor = \lfloor\frac n i\rfloor$$ 那么 $x_{P}$ 也就是 $\frac{n}{\lfloor \frac n i \rfloor}$ 左侧的第一个整点 $\lfloor \frac{n}{\lfloor \frac n i \rfloor}\rfloor$ 即为这些点里的最大整数点。 证毕。 **复杂度证明：** 当 $x \in [1, \lfloor\sqrt n\rfloor]$ 这个区间，最多有 $\lfloor\sqrt n\rfloor$ 种取值。 当 $x \in (\lfloor\sqrt n\rfloor,n]$ 这个区间，$\lfloor\frac n x\rfloor$ 显然只能取到 $[1, \lfloor\sqrt n\rfloor)$这个区间，最多有 $\lfloor\sqrt n\rfloor$ 种取值。 则至多有 $2\lfloor\sqrt n\rfloor$ 种取值，复杂度为 $O(\sqrt n)$。 **代码：** 给出整数 $n$，求 $\sum_{i=1}^n \lfloor\frac{n}{i}\rfloor$。 我们枚举每一段区间，那么当前区间右节点 $+1$ 就是下个区间的左节点： ```cpp for(int l = 1, r; l <= n; l = r + 1) { r = n / (n / l); ans += (r - l + 1) * (n / l) } ``` **练习题：** [P3935 Calculating](https://www.luogu.com.cn/problem/P3935) 一道比较模板的题，显然题目中的 $f(x)$ 就是 $x$ 的约数个数，设 $g(x)=\sum_{i = 1} ^x f(i)$， 那么有一个常见套路： $$\sum_{i=l}^r f(i)=g(r) - g(l-1)$$ 那么我们推一下 $g(x)$： $$g(x)=\sum_{i = 1} ^x f(i)=\sum_{i = 1} ^x \sum_{k = 1} ^x [i\mid k]=\sum_{i=1}^x\lfloor\frac x i\rfloor$$ 大致的意思就是枚举一下 $i\in[1,x]$，看 $i$ 在 $[1,x]$ 中是多少个数的约数，然后加起来就好了，这里有个结论： $$\sum_{i=1}^n[x \mid i] =\lfloor\frac n x\rfloor $$ 然后这个 $g(l - 1)$ 和 $g(r)$ 分别整除分块推一下就好，复杂度 $O(\sqrt n)

代码：

#include <stdio.h>
#define ll long long
#define mod 998244353

ll get(ll x) {
    ll ans = 0;

    for(ll l = 1, r; l <= x; l = r + 1) {
        r = x / (x / l);
        ans = (ans + (r - l + 1) * (x / l)) % mod;
    }

    return ans;
}

int main() {
    ll l, r; scanf("%lld%lld", &l, &r);
    return printf("%lld", (get(r) - get(l - 1) + mod) % mod), 0;
}

P2261 [CQOI2007]余数求和

简单推下式子：

\begin{aligned} G(n,k)&=\sum_{i=1}^n k\bmod i \\ &=\sum_{i=1}^n ( k- i\lfloor\frac k i\rfloor) \\ &=nk - \sum_{i=1}^{n} i\lfloor\frac k i\rfloor \\ &=nk-\sum_{(l,r)} (\sum_{i=l}^r i)\lfloor\frac k l\rfloor \\ &=nk-\sum_{(l,r)} \frac {(r - l + 1)(l + r)} 2 \lfloor\frac k l\rfloor \end{aligned}

这里代码中有个细节，就是 l>k 时 \lfloor\frac k l\rfloor=0，那么 \lfloor \frac k{\lfloor\frac k l\rfloor}\rfloor = \inf 会爆炸，特判一下即可。

代码：

#include <stdio.h>
#define ll long long

ll min(ll a, ll b) { return a < b ? a : b; }

int main() {
    ll n, k, res = 0; scanf("%lld%lld", &n, &k);
    for(ll l = 1, r; l <= n; l = r + 1) {
        r = k / l ? min(n, k / (k / l)) : n;  
        res += (k / l) * (r - l + 1) * (l + r) / 2; 
    }
    return printf("%lld", n * k - res), 0;
} 

AT2300 [ARC068C] Snuke Line

这道题不是那么板了，当 d 取 x 时，[l,r] 能取到的必要条件是：

l\leq xp\leq r

其中 p 是任意正整数，推一下得到：

\lfloor\frac l x\rfloor \leq p\leq\lfloor\frac r x\rfloor \lfloor\frac {l-1} x\rfloor < p\leq\lfloor\frac r x\rfloor

若存在 p，则一定满足：

\lfloor\frac {l-1} x\rfloor < \lfloor\frac r x\rfloor

那么我们只需要求 l,r 能满足的 d 即可。

如果暴力枚举一个 d 显然会超时，我们考虑二维数论分块，即使每一个块内的数除两个数结果都是一定的。

怎么实现的呢？如果我们求出来对于第一个数 x 的右端点是 r_1，对于第二个数 y 的右端点是 r_2，那么我们 r 取 \min(r_1,r_2) 即可使块内除两个数结果都使一定的。

如果当前块 a 满足我们求出来的条件（\lfloor\frac {l-1} x\rfloor < p\leq\lfloor\frac r x\rfloor），那么这一段对 d \in [l_a,r_a] 都有贡献，我们差分一下即可。

在此处还需加上一个剪枝，当 l < l_a\leq r 时， \lfloor\frac l {l_a}\rfloor = 0< \lfloor\frac r {l_a}\rfloor，这一段一定都满足。

代码：

#include <stdio.h>
#define Maxm 1000005

int min(int a, int b) { return a < b ? a : b; }
int d[Maxm];

int main() {
    int n, m, x, y; scanf("%d%d", &n, &m);

    for(int i = 1; i <= n; ++ i) {
        scanf("%d%d", &x, &y); x --;

        for(int l = 1, r; l <= x; l = r + 1) {
            r = min(x / (x / l), y / (y / l));
            if(((x - 1) / l) < (y / l)) d[l] ++, d[r + 1] --; 
        }

        d[x + 1] ++, d[y + 1] --;
    }

    for(int i = 1, p = 0, ans = 0; i <= m; ++ i) {
        ans += d[i];
        printf("%d\n", ans);    
    }

}