题外话：

更好的阅读体验请点这里

如果本文图片炸了，请到上面链接去看。。。。

本文为博主原创文章，转载请附上博文链接！https://www.cnblogs.com/yexinqwq/p/10086668.html

其实回文自动机跟其他自动机差不太多吧，（特别是模板代码短qwq）

如果有任何错误或着有更好的理解，请联系我！

前置知识：

1、马拉车算法（大概吧，其实个人认为不学也没关系qwq）

2、Trie

关于回文自动机：

回文自动机其实就是回文树，是由俄罗斯人MikhailRubinchik于2014年夏发明的，然而关于回文自动机，其实它并不是严谨的树形结构，因为它有两棵子树，其中一颗节点编号为0，它的子树是长度为偶数的回文串，并且这个节点长度设为0，而另一棵子树编号为1，它的子树是长度为奇数的回文串，特别的是：它的长度设置为-1！！！（至于为什么，因为它可以方便代码书写，以后会提到）

变量声明：

1、ch[n][c]：普通的字典树

2、fail[n]：fail指针，指向当前回文串的最长回文后缀，后面会详细介绍

3、len[n]：存放当前节点回文串的长度

4、last：最新添加的回文节点

5、cnt：总的节点个数

声明：

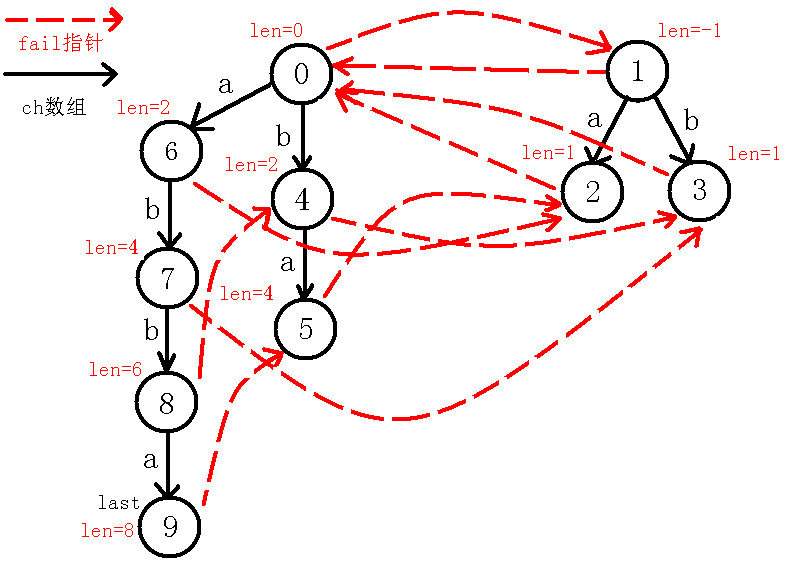
对于一个节点，我不称它为当前节点的编号！而是把每个节点当做一个回文串！例如abbaabba这个例子，完整的回文自动机如下（省略fail指针）：

在上图中，我们对5号节点不叫它5号节点，而叫它abba，（请记住，因为后文这样便于理解），这样叫的原因是0节点经过了b的转移到了4号节点，而就相当于在原来的基础上前后各增加了一个b，即4号节点叫做bb，同样，4号节点经过a的转移到了5号节点，就在前后各加一个a，即abba。但是需要注意的是，因为1号节点len为-1，而每次长度添加都添加2个，所以这样就可以保证1的子树中的长度都为奇数，这就是1号节点len为-1的好处，（如果是现在不懂没有关系，请跟着下面的图解一步一步思考！！！）

大概流程：

在图解之前，还是要让你们朦胧中有一丝印象，知道每步在干吗！（所以这里没看懂的话没关系，到了图解那里一起来理解！），建立回文自动机的过程如下：

初始化：

$fail[0]=1$，$cnt=1

1、找到最新建立的节点last，找到以last结尾的最长回文串的开头-1的位置，如果和当前位置字符相同的话（假设当前字符为x），说明在last这个回文串的基础上两边都有字符x，也就是说会有一个本质不同的回文串产生，否则跳fail指针，找到以last点结尾的最长回文后缀（不包括自身），最终找到last如果last节点没有x的转移，那么我们就让cnt自增1，即新建了一个节点，len[cnt]=len[last]+2因为我们找到last两边都是x字符，所以新的回文节点长度为原来的+2

2、如果last节点没有x的转移，那么我们就让cnt自增1，即新建了一个节点，len[cnt]=len[last]+2因为我们找到last两边都是x字符，所以新的回文节点长度为原来的+2，同时定义j为fail[last]，找到以当前节点的最长回文后缀，使fail[cnt]指向它。

3、更新last节点，继续插入下一个字符。

先贴代码，方便以后查看：

scanf("%d",&n);
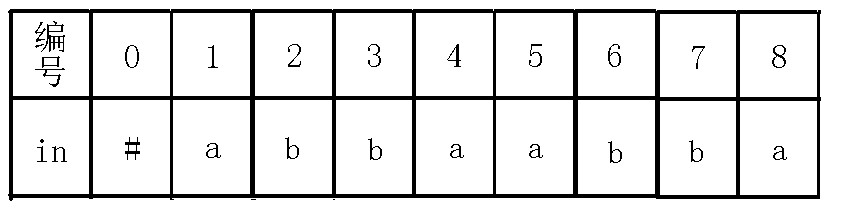
　　scanf("%s",in+1);
　　in[0]='#';
    fail[0]=1;len[1]=-1;//初始化
    for(int i=1;i<=n;i++)
    {
        int j;
        while(in[i-len[last]-1]!=in[i])
            last=fail[last];//匹配（后面会详细解说）
        if(!ch[last][in[i]-'a'])//新建节点
        {
            len[++cnt]=len[last]+2;//长度比原来多2
            j=fail[last];
            while(in[i-len[j]-1]!=in[i])
                j=fail[j];
            fail[cnt]=ch[j][in[i]-'a'];
            ch[last][in[i]-'a']=cnt;
        }
        last=ch[last][in[i]-'a'];
    }
    printf("%d",ans);

如何构建fail指针以及为什么要这样构建：

回文自动机其实是找回文串的，那么怎么样才能找回文串呢？我们假设现在已插入的字符串为babba，而我们现在要插入字符b，我们用肉眼可以发现babbab会是一个新的回文串，那么它是怎么构成的呢，我们可以发现它其实是原来的字符串babba的最长回文后缀abba两端各加上b构成的，而为什么要找最长回文后缀呢?

1. 为什么要最长:
   那么我们思考，假如上面的babba的最长回文后缀我们不当做是abba，而是a，那么它的两端都会是b，也会构成一个回文串bab，但是！如果最长回文后缀是abba的话，两端匹配后，会出现babbab这个回文串，并且！它的最长回文后缀就是bab，也就是说最长会保证每个回文串都在失配的情况被遍历，如果失配了，就继续找当前串的最长回文后缀（不包括自身）
2. 为什么要回文：
   其实这个问题很简单，如果中间不回文的话，就算两边字符相同，构成的新串也不会是回文的
3. 为什么要后缀：
   因为新的字符必须得跟以前插入的回文串相联系，如果是babbac，而你要插入b，如果你找的是abba最长的回文但不是后缀，那么其实是匹配不到的，因为它们没有联系。

   强势图解开始！！！

首先我们初始化s[0]='#'，fail[0]=1，cnt=1，也就是下图：

1、插入字符a

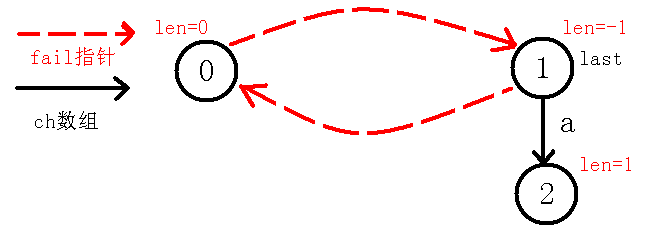
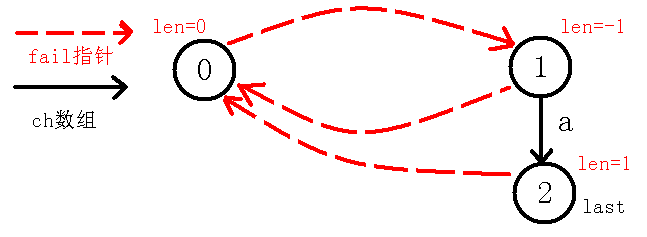
  现在我们考虑求出$cnt$节点（$2$节点）的$fail$指针，我们要知道$fail$指针指向当前节点的最长回文后缀（不包括自己），我们可以看到当前节点就是$a$，没有不包括自己的回文后缀，所以$fail$指针指向$0$，可以看着代码模拟一下，最后会是$0$节点，那么我们再更新$last$到当前节点，最后如下图：   2、插入$b$字符 $last$节点为$2$号节点，那么$in[i-len[last]-1]!=in[i]$，即$in[0]!=in[2]$，这个时候我们判断的其实是在$a$的两边是不是都是$b$，如果是的话那么肯定是回文串，可是这里并不匹配，所以$last$跳$fail$指针到$0$节点，但是我们发现$in[i-len[last]-1]!=in[i]$，即$in[1]!=in[2]$，这个时候我们判断的实质是，我们把回文串的范围由刚才的$3$个变为了$2$个，现在考虑是不是有两个$a$在一起构成回文串，可是还是失配了，所以我们再跳$fail$指针到$1$节点，而这时其实就是自己匹配自己了，也就是$in[2]=in[2]$，所以$len[3]=len[1]+2$，也就是1，因为这个回文串就$b$自身，长度自然为$1$，我们像上面一样连边：   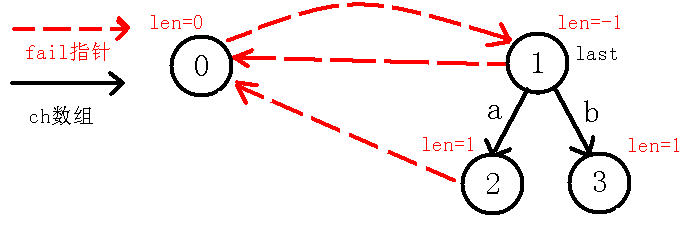我们像上面一样求$b$点的$fail$指针，因为我们需要找到$b$的最长回文后缀，但是我们可以直接看出，除了自身之外就没有回文后缀了，所以它的$fail$指针指向$0$节点，并且下移$last$节点到$3$，自己模拟代码也可以知道，如下图：   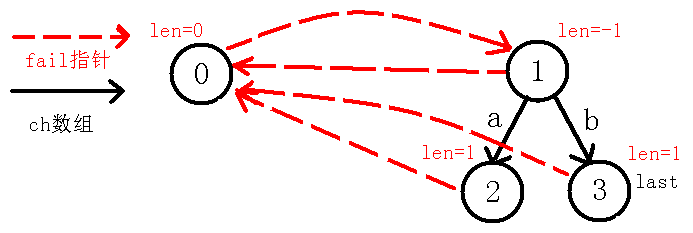3、插入字符$b$： 我们看到$last$节点，而此时我们发现$in[i-len[last]-1]!=in[i]$，即$in[1]!=in[3]$，也就是在考虑在$3$节点（也就是回文串$b$）的左右是不是都是字符$b$，如果是的话，那么就找到了更长的回文串，但是现在失配了，所以我们$last$跳$fail$指针到$0$节点，此时$in[i-len[last]-1]=in[i]$了，也就是$in[2]=in[3]$，也就是说我们找到了一个长度为$2$的回文串$bb$，而$0$节点没有向$b$的转移，于是我们就连一条$b$的转移到新的节点，此节点表示回文串$bb$，如下图：   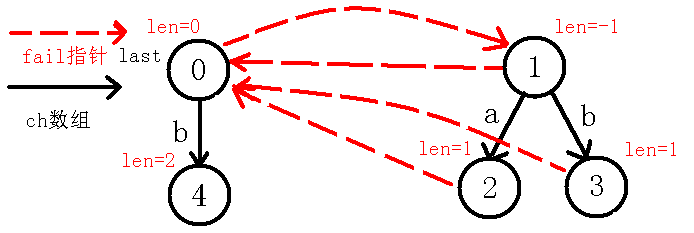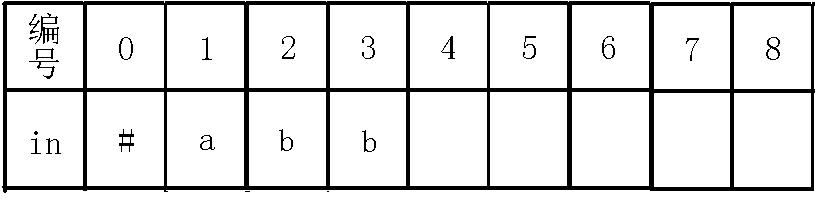那么我们考虑求出$4$号节点的$fail$指针，我们可以看出除了自身回文串($bb$)之外，是它的回文后缀的就是它的最后一个字母$b$，那么我们就应该指向已有的代表$b$这个回文串的节点，即$3$号节点，至于怎么找的后文的例子可以更形象的说明！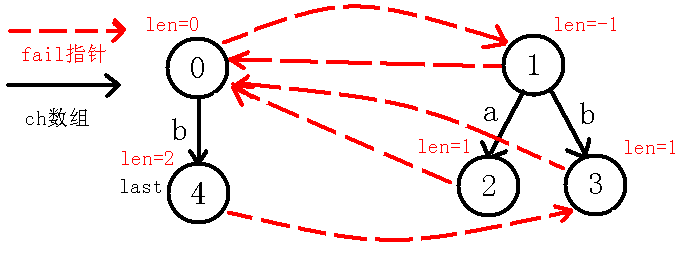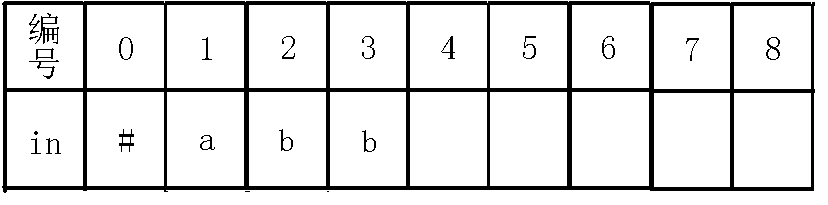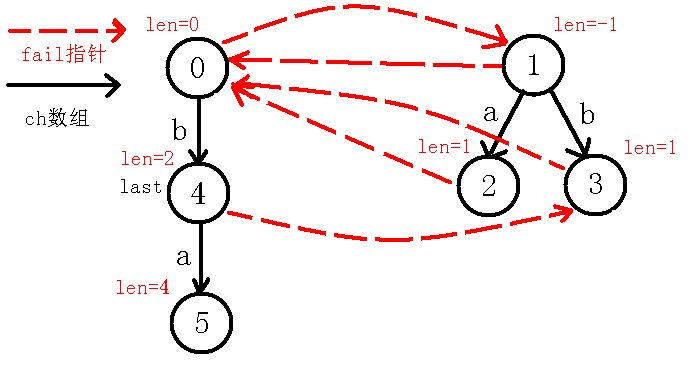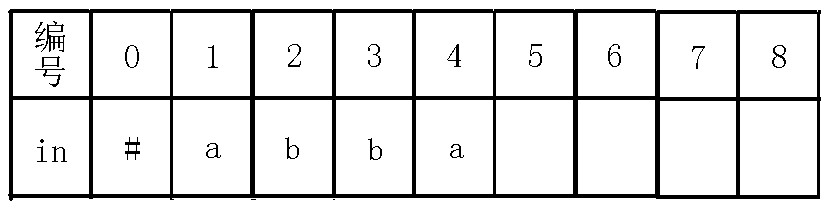所以这里不再赘述，最后更新$last$，操作完后如下：   4、插入$a$字符： 我们看着现在的$last$节点，可以看出$in[i-len[last]-1]=in[i]$，即$in[1]=in[4]$，也就是说，我们在$last$节点的基础上，即回文串$bb$的两边都找到了字符$a$，可以构成一个新的长度为$4$的回文串，而$last$节点没有$a$的转移，于是就新建节点，并连边，如下图：   **【重点】**： 那么，我们现在考虑求出$5$号节点的$fail$指针，$fail$指针是要求出当前回文串的不包括自己的最长回文后缀，因为现在$last$节点在$4$号节点，我们定义一个新的变量$j$来跳$fail$指针，跳到$3$号节点，不让$last$改变，（可能会有人问为什么先跳$fail$再判断呢，为什么不先判断$4$号节点即$in[1]=in[4]$，而要先跳到$3$节点去判断呢？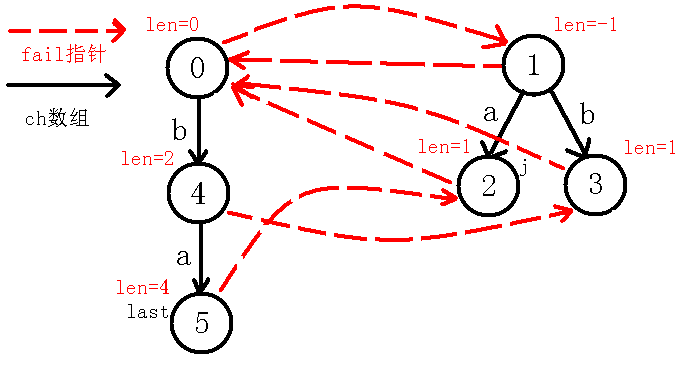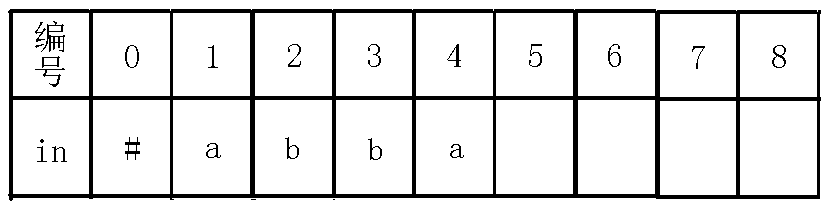那是因为判断$4$号节点其实就是本身这个回文串，即$abba$，而我们说$fail$指针指向的是不包括自己的最长回文后缀），那么我们$j$跳到$3$节点之后发现$in[i-len[j]-1]!=in[i]$即$in[2]!=in[4]$，也就是串$bba$不是回文串,我们再跳$fail$指针到$0$节点，此时$in[i-len[j]-1]!=in[i]$也就是$in[3]!=in[4]$，因为$ba$不是回文串，继续跳$fail$指针，我们到了$1$节点，判断此时的$in[i-len[j]-1]=in[i]$（一定会等于的，因为现在是自己匹配自己，即$in[4]=in[4]$），说明$5$号节点的最长回文后缀为$a$，所以指向代表回文串$a$的节点，即$2$号节点，并且更新$last$节点，如下图：   5、插入$a$字符： 我们继续像上面一样模拟，看到$last$节点，我们发现$in[i-len[last]-1]!=in[i]$，也就是$in[0]!=in[5]$，我们这个操作实际上是找$abba$ 两端是否相同，如果相同则说明能够成新的回文串，然而失配了。。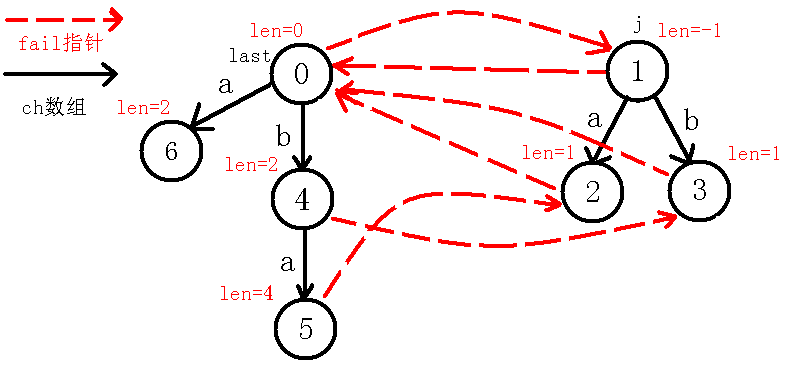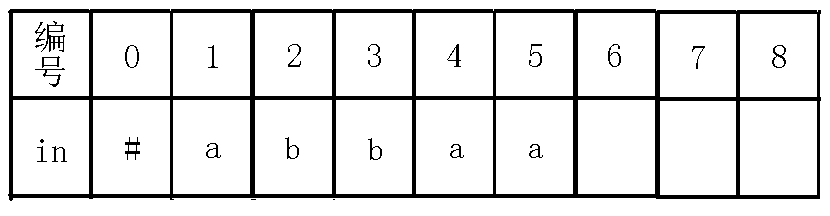于是我们继续跳$fail$指针，到了$2$号节点，我们发现$in[i-len[last]-1]!=in[i]$，即$in[3]!=in[5]$，也就是$a$的两端相不相等，我们又发现不相等，于是又跳$fail$指针，到了$0$节点，我们发现此时$in[i-len[last]-1]=in[i]$，也就是$in[4]=in[5]$，说明我们找到了新的回文串$aa$，而$last$节点并没有$a$的转移（也就是以前没找到回文串$aa$ ），我们新加一条边到新的节点，如下图：   我们继续向上面一样求$fail$指针，$j$跳$fail$指针到$2$号节点，而此时$in[i-len[j]-1]=in[1]$也就是$in[5]=in[5]$，即自己匹配了自己，所以回文串$aa$的除自身外最长回文后缀就是$a$，所以$fail[5]$为表示回文串$a$的节点，即$2$号节点，同时下移$last$，操作完后如下图：   （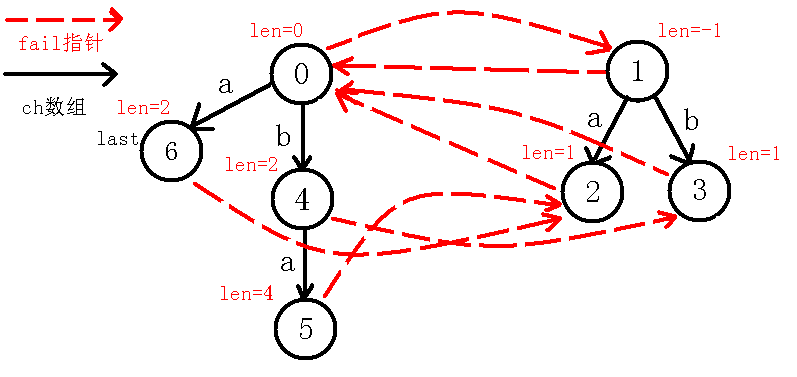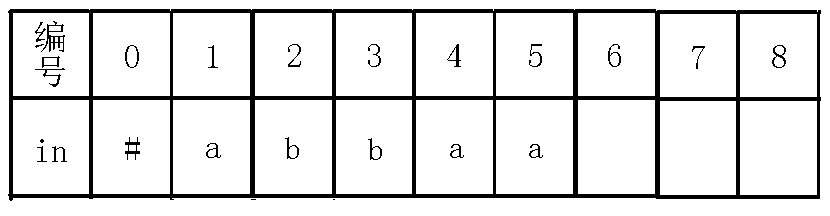后文的插入就留给你们自己动手模拟了，本人就贴个图了，我觉得应该要给你们自己动手实战一下，其实是本人太懒$qwq$） 6、插入$b$字符   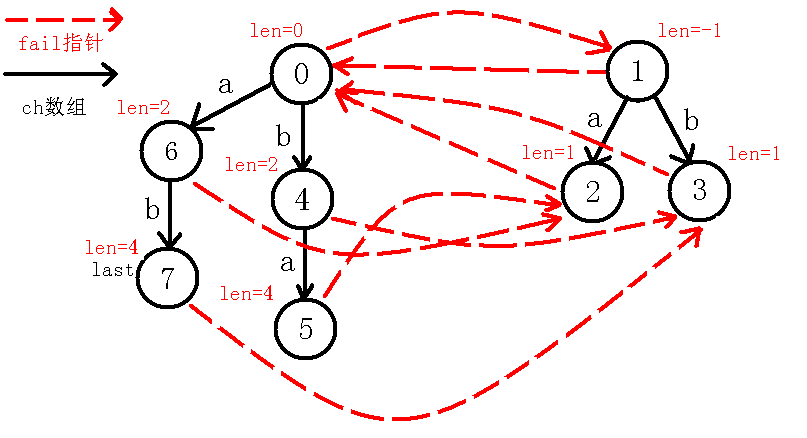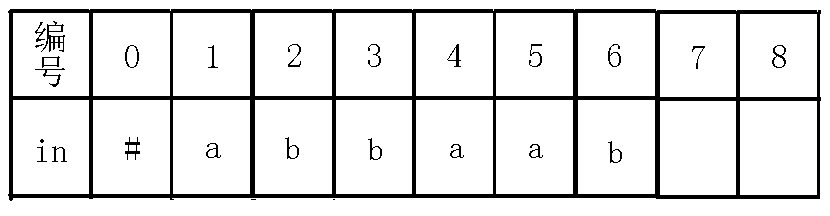7、插入$b$字符   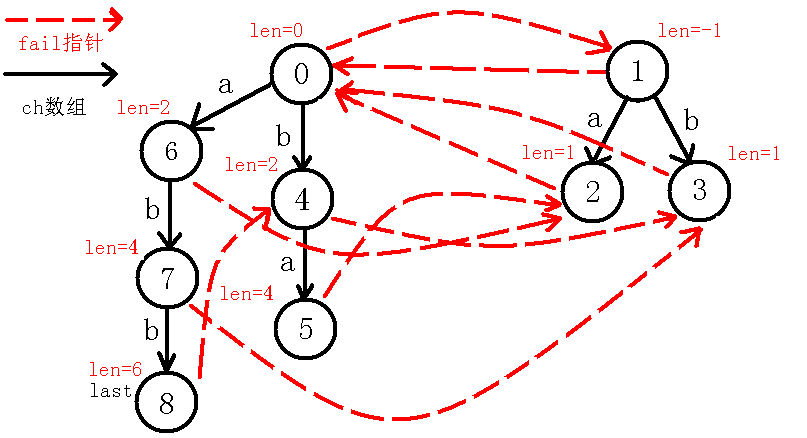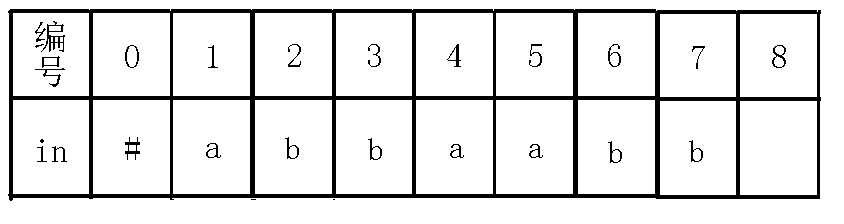8、插入$a$字符：   **** # 尾声： 本篇文章到此结束，如果觉得有帮助的话，希望能够点个赞$qwq