矩阵树定理学习笔记
2021CHD
2024-07-31 22:09:36
浅浅学习了一下矩阵树定理(Matrix-Tree 定理),记录一下学习笔记。
# 前置知识
[图论基础](https://oi.wiki/graph/concept/)
[树](https://oi.wiki/graph/tree-basic/)
[矩阵](https://oi.wiki/math/linear-algebra/matrix/)
[行列式](https://oi.wiki/math/linear-algebra/determinant/)
# 矩阵树定理内容
这里的有向图和无向图的边都**有边权**,并且都**没有自环**,但是**可以有重边**。
## 记号
本文的矩阵**不使用**将元素用方括号包含的形式表示,如 $[3]$ 不能表示唯一一个元素为 $3$ 的 $1$ 阶方阵。
本文中对于集合 $S$,$|S|$ 表示集合 $S$ 所含的元素个数。
$V$ 表示顶点集,$V=\{v_1,v_2,v_3,\dots,v_{|V|}\}$。
$E$ 表示边集,$E=\{e_1,e_2,e_3,\dots,e_{|E|}\}$。
对于一个顶点集为 $V$,边集为 $E$ 的图 $G$,我们记 $G=(V,E)$。
对于无向图 $G=(V,E)$,边 $e_i=(x_i,y_i,w_i)$,表示连接 $v_{x_i}$ 和 $v_{y_i}$,并有 $w_i$ 的边权。
对于有向图 $G=(V,E)$,边 $e_i=(x_i,y_i,w_i)$,表示连接 $v_{x_i}$ 和 $v_{y_i}$,方向从 $v_{x_i}$ 和 $v_{y_i}$,并有 $w_i$ 的边权。
定义有向图 $G=(V,E)$ 中 $v_i$ 可以到达 $v_j$ 当且仅当 $i=j$ 或存在一条边 $e_k\in E$ 满足 $x_k=i$ 并且 $y_k=j$ 或在有向图 $G$ 中存在 $v_k$,使得 $v_i$ 可以到达 $v_k$ 并且 $v_k$ 可以到达 $v_j$。
$\wedge$ 表示合取运算(逻辑与运算),而 $\vee$ 表示析取运算(逻辑或运算),其中 $\wedge$ 的优先级高于 $\vee$。
定义 $[P]=\left\{\begin{matrix}1&P=\text{true}\\0&P=\text{false}\end{matrix}\right.$,其中 $P$ 是逻辑表达式。
定义矩阵 $A$ 的余子式 $M(A)_{i,j}$ 为将 $A$ 中 $A_{i,j}$ 所在的行和列删去后剩下的子矩阵。
记号讲解完毕,先上定理内容。
## 矩阵树定理一
对于一个点集为 $V$,边集为 $E$ 的**无向图** $G$,我们记 $G=(V,E)$。
定义无向图 $G=(V,E)$ 的邻接矩阵 $A$ 为:
$$
A_{i,j}=\sum_{k=1}^{|E|}w_i[x_k=i\wedge y_k=j\vee x_k=i\wedge y_k=j]
$$
定义无向图 $G=(V,E)$ 的度数矩阵 $D$ 为:
$$
D_{i,j}=\left\{\begin{matrix}0&i\ne j\\\displaystyle\sum_{k=1}^{|E|}w_k[x_k=i\vee y_k=i]&i=j\end{matrix}\right.
$$
其中矩阵 $A$ 和矩阵 $D$ 都是 $|V|$ 阶方阵。
定义无向图 $G=(V,E)$ 的 Laplace 矩阵 $L=D-A$。
定义无向图 $G=(V,E)$ 的一颗生成树为 $T_{G}=(V,E')$,其中 $E'\subseteq E$,并且图 $T_{G}$ 是一颗树。
定义树 $T=(V,E)$ 的权值 $\displaystyle\text{weight}(T)=\prod_{i=1}^{|E|}w_i$。
那么有以下结论:
$$
\sum_{T_G}\text{weight}(T_G)=\det(M(L)_{i,i})
$$
其中 $i$ 是不超过 $|V|$ 的任意正整数。
## 矩阵树定理二
对于一个点集为 $V$,边集为 $E$ 的**有向图** $G$,我们记 $G=(V,E)$。
定义有向图 $G=(V,E)$ 的邻接矩阵 $A$ 为:
$$
A_{i,j}=\sum_{k=1}^{|E|}w_i[x_k=i\wedge y_k=j]
$$
定义有向图 $G=(V,E)$ 的出度矩阵 $D^{\text{out}}$ 为:
$$
(D^{\text{out}})_{i,j}=\left\{\begin{matrix}0&i\ne j\\\displaystyle\sum_{k=1}^{|E|}w_k[x_k=i]&i=j\end{matrix}\right.
$$
定义有向图 $G=(V,E)$ 的入度矩阵 $D^{\text{in}}$ 为:
$$
(D^{\text{in}})_{i,j}=\left\{\begin{matrix}0&i\ne j\\\displaystyle\sum_{k=1}^{|E|}w_k[y_k=i]&i=j\end{matrix}\right.
$$
其中矩阵 $A$,矩阵 $D^{\text{out}}$ 和矩阵 $D^{\text{in}}$ 都是 $|V|$ 阶方阵。
定义有向图 $G=(V,E)$ 的出度 Laplace 矩阵 $L^{\text{out}}=D^{\text{out}}-A$。
定义有向图 $G=(V,E)$ 的入度 Laplace 矩阵 $L^{\text{in}}=D^{\text{in}}-A$。
定义有向图 $G=(V,E)$ 的以 $v_i$ 为根的一颗**内向生成树**为 $T'_{G}(v_i)=(V,E')$,其中 $E'\subseteq E$,$|E'|=|V|-1$,并且在有向图 $T'_{G}(v_i)$ 中,$v_i$ 可以被任何顶点到达。
定义有向图 $G=(V,E)$ 的以 $v_i$ 为根的一颗**外向生成树**为 $T^{*}_{G}(v_i)=(V,E')$,其中 $E'\subseteq E$,$|E'|=|V|-1$,并且在有向图 $T^{*}_{G}(v_i)$ 中,$v_i$ 可以到达任何顶点。
定义有向图 $G=(V,E)$ 的权值 $\displaystyle\text{weight}(G)=\prod_{i=1}^{|E|}w_i$。
那么有以下结论:
$$
\sum_{T'_{G}(v_i)}\text{weight}(T'_{G}(v_i))=\det(M(L^{\text{out}})_{i,i})
$$
$$
\sum_{T^{*}_{G}(v_i)}\text{weight}(T^{*}_{G}(v_i))=\det(M(L^{\text{in}})_{i,i})
$$
其中 $i$ 是不超过 $|V|$ 的任意正整数。
# 证明矩阵树定理
为了证明矩阵树定理,我们要先了解并证明 LGV 引理和柯西-比内公式。
## LGV 引理
LGV 引理(Lindström–Gessel–Viennot lemma)的适用范围是**有向无环图**,边有边权。
### 记号
本文中 $[l,r]$ 代表从 $l$ 到 $r$ 的闭区间,而非 $l$ 和 $r$ 的最小公倍数。
记序列 $S$ 的长度为 $|S|$。
在有向无环图 $G=(V,E)$ 中定义路径 $P=(e_{t_1},e_{t_2},\dots,e_{t_{|P|}})$ 为边的序列,且满足对于任意正整数 $i\in[1,|P|-1]$,$y_{t_i}=x_{t_{i+1}}$。
在有向无环图 $G=(V,E)$ 中定义路径 $P=(e_{t_1},e_{t_2},\dots,e_{t_{|P|}})$ 的起始为 $x_{t_1}$,记作 $\text{start}(P)=x_{t_1}$,终止为 $y_{t_{|P|}}$,记作 $\text{end}(P)=y_{t_{|P|}}$。
有向无环图 $G=(V,E)$ 中的路径 $P$ 可以记作 $P:\text{start}(P)\to \text{end}(P)$。
对于有向无环图 $G=(V,E)$ 中的路径 $P=(e_{t_1},e_{t_2},\dots,e_{t_{|P|}})$,定义顶点 $v_i\in P$ 当且仅当存在不超过 $|P|$ 的正整数 $j$,满足 $x_{t_j}=i$ 或 $y_{t_j}=i$。
对于有向无环图 $G=(V,E)$ 中的顶点集 $V'\subseteq V$ 和路径 $P$,定义路径 $P$ 经过了 $V'$ 当且仅当存在顶点 $v_i\in V'$ 满足 $v_i\in P$。
对于有向无环图 $G=(V,E)$ 中的路径 $P$,若顶点 $v_i\in V$ 满足 $v_i\in P$,则定义 $v_i$ 在 $P$ 中的位置 $\text{pos}(P,v_i)=\left\{\begin{matrix}|P|+1&i=\text{end}(P)\\j&i=x_{t_j}\end{matrix}\right.$。
定义集合 $S$ 的一个置换 $\sigma(S)=(\sigma_1,\sigma_2,\dots,\sigma_{|S|})$ 为一个序列,满足对于所有 $s\in S$,$s\in\sigma(S)$。
特别地,置换 $\sigma(\{1,2,\dots,n\})$ 可以简记为 $\sigma(n)$ 或 $\sigma$,称 $\sigma$ 为从 $1$ 到 $n$ 的排列。
对于从 $1$ 到 $n$ 的排列 $\sigma$,定义逆序对数 $\displaystyle\text{t}(\sigma)=\sum_{i=1}^{n-1}\sum_{j=i+1}^n[\sigma_i>\sigma_j]$。
### 内容
对于有向无环图 $G=(V,E)$ 中的路径 $P$,定义权值 $\displaystyle\text{weight}(P)=\prod_{i=1}^{|P|}w_{t_i}$。
在有向无环图 $G=(V,E)$ 中,取 $V$ 的子集 $A=\{v_{a_1},v_{a_2},\dots,v_{a_{|A|}}\}$ 和 $B=\{v_{b_1},v_{b_2},\dots,v_{b_{|B|}}\}$,使得 $A\cap B=\varnothing$ 并且 $|A|=|B|>0$,定义 $A$ 到 $B$ 的一组路径组 $S=\{P_1,P_2,\dots,P_{|A|}\}$ 为路径的集合,满足其中 $\text{start}(P_i)=a_i$,$\text{end}(P_i)=b_{\sigma_i}$,$\sigma$ 是从 $1$ 到 $|A|$ 的排列,记作 $S:A\to B$ 或 $S(\sigma):A\to B$。
进一步地,若有向无环图 $G=(V,E)$ 中路径组 $S(\sigma):A\to B=\{P_1,P_2,\dots,P_{|A|}\}$ 满足 $\displaystyle\sum_{i=1}^{|V|}\sum_{j=1}^{|A|-1}\sum_{k=j+1}^{|A|}[v_i\in P_j\wedge v_i\in P_k]=0$,则称路径组 $S:A\to B$ 为不相交路径组,记作 $S^{+}:A\to B$ 或 $S(\sigma)^{+}:A\to B$,反之,则称路径组 $S:A\to B$ 为相交路径组,记作 $S^{-}:A\to B$ 或 $S(\sigma)^{-}:A\to B$。
记有向无环图 $G=(V,E)$ 中所有相交路径组 $S^{-}:A\to B$ 构成的集合为 $\mathbb{S}_{A,B}$。
定义有向无环图 $G=(V,E)$ 中路径组 $S:A\to B=\{P_1,P_2,\dots,P_{|A|}\}$ 的权值 $\displaystyle\text{weight}(S)=\prod_{i=1}^{|A|}\text{weight}(P_i)$。
对于有向无环图 $G=(V,E)$ 中任意两顶点 $v_i\in V$ 与 $v_j\in V$ 满足 $i\ne j$,定义 $v_i$ 到 $v_j$ 的路径权值和 $\displaystyle\text{w}(i,j)=\sum_{P:i\to j}\text{weight}(P)$。
在有向无环图 $G=(V,E)$ 中,取 $V$ 的子集 $A=\{v_{a_1},v_{a_2},\dots,v_{a_{|A|}}\}$ 和 $B=\{v_{b_1},v_{b_2},\dots,v_{b_{|B|}}\}$,使得 $A\cap B=\varnothing$ 并且 $|A|=|B|>0$,构造矩阵 $M$ 的方式如下:
$$
M_{i,j}=\text{w}(a_i,b_j)
$$
其中矩阵 $M$ 是 $|A|$ 阶方阵。
有以下结论:
$$
\det(M)=\sum_{S(\sigma)^{+}:A\to B}(-1)^{\text{t}(\sigma)}\text{weight}(S)
$$
### 证明
根据行列式的定义,有:
$$
\begin{aligned}\det(M)&=\sum_{\sigma(|A|)}(-1)^{\text{t}(\sigma)}\prod_{i=1}^{|A|}\text{w}(a_i,b_{\sigma_i})\\&=\sum_{\sigma(|A|)}(-1)^{\text{t}(\sigma)}\prod_{i=1}^{|A|}\sum_{P:a_i\to b_{\sigma_i}}\text{weight}(P)\\&=\sum_{\sigma(|A|)}(-1)^{\text{t}(\sigma)}\sum_{S(\sigma):A\to B}\prod_{i=1}^{|A|}\text{weight}(P_i)\\&=\sum_{\sigma(|A|)}(-1)^{\text{t}(\sigma)}\sum_{S(\sigma):A\to B}\text{weight}(S)\\&=\sum_{\sigma(|A|)}\sum_{S(\sigma):A\to B}(-1)^{\text{t}(\sigma)}\text{weight}(S)\\&=\sum_{S(\sigma):A\to B}(-1)^{\text{t}(\sigma)}\text{weight}(S)\\&=\left(\sum_{S(\sigma)^{+}:A\to B}(-1)^{\text{t}(\sigma)}\text{weight}(S)\right)+\left(\sum_{S(\sigma)^{-}:A\to B}(-1)^{\text{t}(\sigma)}\text{weight}(S)\right)\end{aligned}
$$
接下来只需要证明 $\displaystyle\sum_{S(\sigma)^{-}:A\to B}(-1)^{\text{t}(\sigma)}\text{weight}(S)=0$。
在有向无环图 $G=(V,E)$ 中,考虑对于相交路径组 $S^{-}:A\to B=\{P_1,P_2,\dots,P_{|A|}\}$,选取最小的 $i$ 使得存在 $j\ne i$ 和 $k$,使得 $v_k\in P_i$ 且 $v_k\in P_j$,再选取 $v_k\in P_i$ 且 $v_k$ 在 $P_i$ 中的位置 $\text{pos}(P_i,v_k)$ 最小的 $k$ 使得存在 $j\ne i$,使得 $v_k\in P_j$,最后选取最小的 $j\ne i$,使得 $v_k\in P_j$。
选定 $i$,$k$ 和 $j$ 后,如下图,交换路径 $P_i$ 和 $P_j$ 在顶点 $v_k$ 之后的部分,得到新的 $S':A\to B$,记作 $\text{rev}(S)$,称 $S'$ 是 $S$ 的变换。
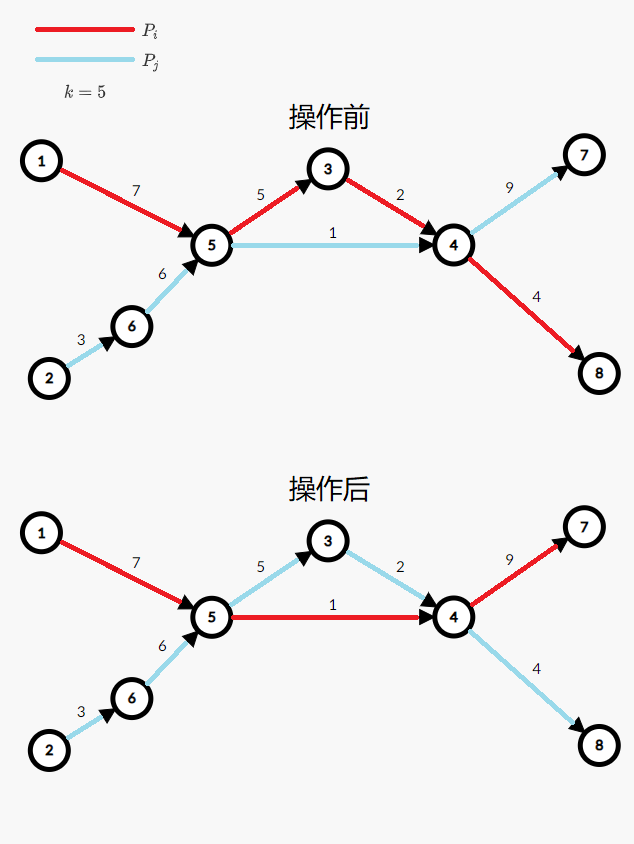
**注意:以下对于图 $G=(V,E)$ 相交路径组 $S^{-}:A\to B$ 的变换 $\text{rev}(S)$ 的形式化定义建议不看。**
> 对于有向无环图 $G=(V,E)$ 中的路径 $P$ 定义子路径 $P[l\sim r]=(e_{t_l},e_{t_l+1},\dots,e_{t_r})$,其中 $1\le l\le r\le |P|$。
>
> 对于有向无环图 $G=(V,E)$ 中的路径 $P=(e_{t_1},e_{t_2},\dots,e_{t_{|P|}})$ 和 $Q=(e_{t'_1},e_{t'_2},\dots,e_{t'_{|P|}})$,若 $\text{end}(P)=\text{start}(Q)$,定义和路径 $P+Q=(e_{t_1},e_{t_2},\dots,e_{t_{|P|}},e_{t'_1},e_{t'_2},\dots,e_{t'_{|P|}})$。
>
> 形式化地,在有向无环图 $G=(V,E)$ 中,对于相交路径组 $S^{-}:A\to B=\{P_1,P_2,\dots,P_{|A|}\}$,计算 $\displaystyle i=\min_{\exists j'(j'\ne i'\wedge\exists k'(v_{k'}\in P_{i'}\wedge v_{k'}\in P_{j'}))}i'$,而后计算 $\displaystyle k=\sum_{k'=1}^{|V|}k'[v_{k'}\in P_i\wedge\exists j'(j'\ne i\wedge v_{k'}\in P_{j'})\wedge\forall k^{*}(v_{k^{*}}\in P_i\wedge\exists j'(j'\ne i\wedge v_{k^{*}}\in P_{j'})\wedge\text{pos}(P_i,v_{k^{*}})\ge\text{pos}(P_i,v_{k'}))]$,最后计算 $\displaystyle j=\min_{j'\ne i\wedge v_k\in P_{j'}}j'$。
>
> 在计算 $i$,$k$ 和 $j$ 后,若 $\text{pos}(P_i,v_k)=|P_i|+1$,则容易得到 $1<\text{pos}(P_j,v_k)<|P_j|+1$,令 $P_i'=P_i+P_j[\text{pos}(P_j,v_k)\sim|P_j|]$,$P_j'=P_j[1\sim\text{pos}(P_j,v_k)-1]$,否则,若 $\text{pos}(P_i,v_k)=1$,则容易得到 $1<\text{pos}(P_j,v_k)<|P_j|+1$,令 $P_i'=P_j[\text{pos}(P_j,v_k)\sim|P_j|]$,$P_j'=P_j[1\sim\text{pos}(P_j,v_k)-1]+P_i$,否则 $1<\text{pos}(P_i,v_k)<|P_i|+1$,若 $\text{pos}(P_j,v_k)=|P_j|+1$,令 $P_i'=P_i[1\sim\text{pos}(P_i,v_k)-1]$,$P_j'=P_j+P_i[\text{pos}(P_i,v_k)\sim|P_i|]$,否则,若 $\text{pos}(P_j,v_k)=1$,令 $P_i'=P_i[1\sim\text{pos}(P_i,v_k)-1]+P_j$,$P_j'=P_i[\text{pos}(P_i,v_k)\sim|P_i|]$,否则 $1<\text{pos}(P_j,v_k)<|P_j|+1$,令 $P_i'=P_i[1\sim\text{pos}(P_i,v_k)-1]+P_j[\text{pos}(P_j,v_k)\sim|P_j|]$,$P_j'=P_j[1\sim\text{pos}(P_j,v_k)-1]+P_i[\text{pos}(P_i,v_k)\sim|P_i|]$。
>
> 则相交路径组 $S$ 的变换 $\text{rev}(S)=(P_1,P_2,\dots,P_{i-1},P_i',P_{i+1},\dots,P_{j-1},P_j',P_{j+1},\dots,P_{|A|})$。(不难证明 $i<j$)
>
> 不难发现,由此定义的 $\text{rev}(S)$ 一定也是 $A$ 到 $B$ 的一组路径组。
不难发现,在有向无环图 $G=(V,E)$ 中,对于任何相交路径组 $S^{-}:A\to B$,其变换 $\text{rev}(S):A\to B$ 一定也是相交路径组,并且一定有 $\text{rev}(S)\ne S$,$\text{rev}(\text{rev}(S))=S$。
则在有向无环图 $G=(V,E)$ 中,作用于相交路径组 $S^{-}:A\to B$ 的函数 $\text{rev}:\mathbb{S}_{A,B}\to \mathbb{S}_{A,B}$ 是双射,其反函数为 $\text{rev}$ 本身。
不难证明,在有向无环图 $G=(V,E)$ 中,对于任何相交路径组 $S^{-}:A\to B$ 和 $M^{-}:A\to B$,若 $S\ne M$,则 $\text{rev}(S)\ne \text{rev}(M)$。
不难证明,在有向无环图 $G=(V,E)$ 中,对于任何相交路径组 $S(\sigma)^{-}:A\to B$ 和其变换 $R(\sigma')^{-}:A\to B$,有 $\text{weight}(S)=\text{weight}(R)$ 且 $(-1)^{\text{t}(\sigma)}+(-1)^{\text{t}(\sigma')}=0$。
根据上述结论,有:
$$
\begin{aligned}&\sum_{S(\sigma)^{-}:A\to B}(-1)^{\text{t}(\sigma)}\text{weight}(S)\\=&\frac{1}{2}\sum_{S(\sigma)^{-}:A\to B}(-1)^{\text{t}(\sigma)}\text{weight}(S)+\frac{1}{2}\sum_{S(\sigma)^{-}:A\to B}(-1)^{\text{t}(\sigma)}\text{weight}(S)\\=&\frac{1}{2}\sum_{S(\sigma)^{-}:A\to B}(-1)^{\text{t}(\sigma)}\text{weight}(S)-\frac{1}{2}\sum_{S(\sigma)^{-}:A\to B}(-1)^{\text{t}(\sigma)}\text{weight}(\text{rev}(S))\\=&\frac{1}{2}\sum_{S(\sigma)^{-}:A\to B}(-1)^{\text{t}(\sigma)}\text{weight}(S)-(-1)^{\text{t}(\sigma)}\text{weight}(\text{rev}(S))\\=&\frac{1}{2}\sum_{S(\sigma)^{-}:A\to B}(-1)^{\text{t}(\sigma)}(\text{weight}(S)-\text{weight}(\text{rev}(S)))\\=&0\end{aligned}
$$
则有:
$$
\begin{aligned}\det(M)&=\left(\sum_{S(\sigma)^{+}:A\to B}(-1)^{\text{t}(\sigma)}\text{weight}(S)\right)+\left(\sum_{S(\sigma)^{-}:A\to B}(-1)^{\text{t}(\sigma)}\text{weight}(S)\right)\\&=\left(\sum_{S(\sigma)^{+}:A\to B}(-1)^{\text{t}(\sigma)}\text{weight}(S)\right)+0\\&=\sum_{S(\sigma)^{+}:A\to B}(-1)^{\text{t}(\sigma)}\text{weight}(S)\end{aligned}
$$
至此,LGV 引理得证。
## 柯西-比内公式
### 记号
若 $n$ 为正整数,记集合 $\{1,2,\dots,n\}$ 为 $[n]$,特别地,$[0]$ 表示空集 $\varnothing$。
定义从 $1$ 到 $n$ 的排列 $\sigma$ 和 $\sigma'$ 的乘积 $\sigma\circ\sigma'=(\sigma_{\sigma'_1},\sigma_{\sigma'_2},\dots,\sigma_{\sigma'_n})$ 为一个从 $1$ 到 $n$ 的排列,运算 $\circ$ 称为置换的乘法,容易得到置换的乘法满足交换律和结合律。
对于 $n\times m$ 矩阵 $A$,对于集合 $S_1\subseteq[n]$ 和集合 $S_2\subseteq[m]$,若 $S_1\ne\varnothing$ 且 $S_2\ne\varnothing$,记矩阵 $A$ 选取元素 $A_{i,j}$ 其中 $i\in S_1$,$j\in S_2$ 组成的子矩阵记为 $A_{S_1,S_2}$。
设 $A$ 为 $n\times m$ 矩阵而 $B$ 为 $m\times n$ 矩阵。
### 内容
柯西-比内公式(Cauchy–Binet formula)的内容如下:
$$
\det(AB)=\sum_{|S|=n\wedge S\subseteq[m]}\det(A_{[n],S})\det(B_{S,[n]})
$$
其中 $S=\{s_1,s_2,\dots,s_n\}$ 为集合。
### 证明
要证明柯西-比内公式,需要构造**有向无环图** $G=(V,E)$,其中 $V=\{v_{1,1},v_{1,2},\dots,v_{1,n},v_{2,1},v_{2,2},\dots,v_{2,m},v_{3,1},v_{3,2},\dots,v_{3,n}\}$,$E=\{e_{1,1,1},e_{1,1,2},\dots,e_{1,1,m},e_{1,2,1},\dots,e_{1,n,m},e_{2,1,1},e_{2,1,2},\dots,e_{2,1,n},e_{2,2,1},\dots,e_{2,m,n}\}$。
其中有向边 $e_{1,i,j}(1\le i\le n,1\le j\le m)$ 连接 $v_{1,i}$ 和 $v_{2,j}$,方向从 $v_{1,i}$ 到 $v_{2,j}$,边权为 $A_{i,j}$。
其中有向边 $e_{2,i,j}(1\le i\le m,1\le j\le n)$ 连接 $v_{2,i}$ 和 $v_{3,j}$,方向从 $v_{2,i}$ 到 $v_{3,j}$,边权为 $B_{i,j}$。
在有向无环图 $G$ 中记顶点集 $V_1=\{v_{1,1},v_{1,2},\dots,v_{1,n}\}$,$V_2=\{v_{2,1},v_{2,2},\dots,v_{2,m}\}$,$V_3=\{v_{3,1},v_{3,2},\dots,v_{3,n}\}$,$V_S=\{v_{2,i}|i\in S\}$。
记 $M=AB$,不难发现 $M$ 为 $n$ 阶方阵且 $M_{i,j}$ 等于 $v_{1,i}$ 到 $v_{3,j}$ 的路径权值和。
则根据 LGV 引理,有:
$$
\det(M)=\det(AB)=\sum_{S(\sigma)^{+}:V_1\to V_3}(-1)^{\text{t}(\sigma)}\text{weight}(S)
$$
对于 $A_{[n],S}$ 和 $B_{S,[n]}$,同样有 $(A_{[n],S})_{i,j}$ 等于 $v_{1,i}$ 到 $v_{2,s_i}$ 的路径权值和,$(B_{S,[n]})_{i,j}$ 等于 $v_{2,s_i}$ 到 $v_{3,i}$ 的路径权值和。
根据 LGV 引理,同样有:
$$
\det(A_{[n],S})=\sum_{R(\sigma)^{+}:V_1\to V_S}(-1)^{\text{t}(\sigma)}\text{weight}(R)
$$
$$
\det(B_{S,[n]})=\sum_{R(\sigma)^{+}:V_S\to V_3}(-1)^{\text{t}(\sigma)}\text{weight}(R)
$$
由于 $V_1$ 中的顶点到 $V_3$ 中的顶点的路径必然会经过 $V_2$,有:
$$
\begin{aligned}&\sum_{|S|=n\wedge S\subseteq[m]}\det(A_{[n],S})\det(B_{S,[n]})\\=&\sum_{|S|=n\wedge S\subseteq[m]}\left(\sum_{R(\sigma)^{+}:V_1\to V_S}(-1)^{\text{t}(\sigma)}\text{weight}(R)\right)\left(\sum_{R(\sigma)^{+}:V_S\to V_3}(-1)^{\text{t}(\sigma)}\text{weight}(R)\right)\\=&\sum_{|S|=n\wedge S\subseteq[m]}\sum_{R(\sigma)^{+}:V_1\to V_S}(-1)^{\text{t}(\sigma)}\text{weight}(R)\sum_{R'(\sigma')^{+}:V_S\to V_3}(-1)^{\text{t}(\sigma')}\text{weight}(R')\\=&\sum_{|S|=n\wedge S\subseteq[m]}\sum_{R(\sigma)^{+}:V_1\to V_S}\sum_{R'(\sigma')^{+}:V_S\to V_3}(-1)^{\text{t}(\sigma)+\text{t}(\sigma')}\text{weight}(R)\text{weight}(R')\\=&\sum_{\sigma(n)}\sum_{\sigma'(n)}\sum_{|S|=n\wedge S\subseteq[m]}\sum_{R(\sigma)^{+}:V_1\to V_S}\sum_{R'(\sigma')^{+}:V_S\to V_3}(-1)^{\text{t}(\sigma)+\text{t}(\sigma')}\text{weight}(R)\text{weight}(R')\\=&\sum_{\sigma(n)}\sum_{\sigma'(n)}\sum_{R(\sigma\circ\sigma')^{+}:V_1\to V_3}(-1)^{\text{t}(\sigma)+\text{t}(\sigma')}\text{weight}(R)\end{aligned}
$$
所以接下来只需证明 $(-1)^{\text{t}(\sigma(n))+\text{t}(\sigma'(n))}=(-1)^{\text{t}(\sigma\circ\sigma')}$ 即可。
**关于这一点的证明,由于涉及[群论](https://oi.wiki/math/group-theory/)相关内容,请选择性阅读。**
> 记所有从 $1$ 到 $n$ 的排列 $\sigma$ 组成的集合为 $U_n$。
>
> 有 $n$ 元对称群 $S_n=(U_n,\circ)$,$S_n$ 是阿贝尔群。
>
> 所有 $\text{t}(\sigma)$ 是偶数的置换 $\sigma$ 称为偶置换,记作 $\sigma^{+}$,$\text{t}(\sigma)$ 是奇数的置换称为奇置换,记作 $$\sigma^{-}$$。
>
> 记所有有 $n$ 个元素的偶置换 $\sigma^{+}$ 组成的集合为 $W_n$。
>
> $n$ 元交错群 $A_n=(W_n,\circ)$ 是 $n$ 元对称群的子群。
>
> 有二阶群 $Q=(\{1,-1\},\times)$,单位元为 $1$。
>
> 存在从 $S_n$ 到 $Q$ 的群同态 $\text{sgn}:S_n\to Q$,满足 $A_n$ 为该群同态的核,也就是说 $\text{sgn}(\sigma(n))=\left\{\begin{matrix}1&\sigma\in W_n\\-1&\sigma\notin W_n\end{matrix}\right.$ 满足 $\text{sgn}(\sigma(n)\circ\sigma'(n))=\text{sgn}(\sigma(n))\times\text{sgn}(\sigma'(n))$。
>
> 容易看出 $\text{sgn}(\sigma(n))=(-1)^{\text{t}(\sigma)}$,则得到 $(-1)^{\text{t}(\sigma(n))}\times(-1)^{\text{t}(\sigma'(n))}=(-1)^{\text{t}(\sigma\circ\sigma')}$,即$(-1)^{\text{t}(\sigma(n))+\text{t}(\sigma'(n))}=(-1)^{\text{t}(\sigma\circ\sigma')}$。
证明上述结论后,则有:
$$
\begin{aligned}&\sum_{\sigma(n)}\sum_{\sigma'(n)}\sum_{R(\sigma\circ\sigma')^{+}:V_1\to V_3}(-1)^{\text{t}(\sigma)+\text{t}(\sigma')}\text{weight}(R)\\=&\sum_{\sigma(n)}\sum_{\sigma'(n)}\sum_{R(\sigma\circ\sigma')^{+}:V_1\to V_3}(-1)^{\text{t}(\sigma\circ\sigma')}\text{weight}(R)\\=&\sum_{S(\sigma)^{+}:V_1\to V_3}(-1)^{\text{t}(\sigma)}\text{weight}(R)\\=&\det(AB)\end{aligned}
$$
柯西-比内公式得证。
## 证明矩阵树定理一
对于无向图 $G=(V,E)$,其 Laplace 矩阵为矩阵 $L$。
构造 $|V|\times|E|$ 矩阵 $C$ 的方式如下:
$$
C_{i,j}=\left\{\begin{matrix}\sqrt{w_j}&i=x_j\\-\sqrt{w_j}&i=y_j\\0&i\ne x_j\wedge i\ne y_j\end{matrix}\right.
$$
设 $L'=CC^{T}$,其中 $C^{T}$ 表示矩阵 $C$ 的转置,根据矩阵乘法的定义有 $L'$ 为 $|V|$ 阶方阵,$\displaystyle L'_{i,j}=\sum_{k=1}^{|E|}C_{i,k}(C^{T})_{k,j}=\sum_{k=1}^{|E|}C_{i,k}C_{j,k}$。
当 $i=j$ 时,有:
$$
\begin{aligned}&L'_{i,j}\\=&L'_{i,i}\\=&\sum_{k=1}^{|E|}C_{i,k}C_{i,k}\\=&\sum_{k=1}^{|E|}(C_{i,k})^2\\=&\sum_{k=1}^{|E|}w_k[i=x_k\vee i=y_k]\\
=&L_{i,i}\end{aligned}
$$
当 $i\ne j$ 时,有:
$$
\begin{aligned}&L'_{i,j}\\=&\sum_{k=1}^{|E|}C_{i,k}C_{k,j}\\=&\sum_{k=1}^{|E|}-w_k[i=x_k\wedge i=y_k\vee i=y_k\wedge i=x_k]\\=&L_{i,j}\end{aligned}
$$
那么 $CC^{T}=L$。
若 $S_1$ 与 $S_2$ 均为集合,则 $S_1-S_2$ 表示集合的差(简称差集)。
设矩阵 $B_i=C_{[|V|]-\{i\},[|E|]}$。
不难证明 $B_i(B_i)^{T}=M(L)_{i,i}$。
那么根据柯西-比内公式,有:
$$
\begin{aligned}&\det(M(L)_{i,i})\\=&\det(B_i(B_i)^{T})\\=&\sum_{|S|=|V|-1\wedge S\subseteq[|E|]}\det((B_i)_{[|V|-1],S})\det(((B_i)^{T})_{S,[|V|-1]})\\=&\sum_{|S|=|V|-1\wedge S\subseteq[|E|]}\det((B_i)_{[|V|-1],S})\det((B_i)_{[|V|-1],S})\\=&\sum_{|S|=|V|-1\wedge S\subseteq[|E|]}\det((B_i)_{[|V|-1],S})^2\end{aligned}
$$
考虑当 $|S|=|V|-1$ 且 $S\subseteq[|E|]$ 时 $\det((B_i)_{[|V|-1],S})^2$ 的意义。
不难想到,集合 $S$ 的意义就是从 $|E|$ 条边中选出 $|V|-1$ 条边,记选出的边集为 $E'=\{e_j\in E|j\in S\}$。
若无向图 $G$ 的生成子图 $G'=(V,E')$ 不是图 $G$ 的生成树,则无向图 $G'$ 一定不是连通图。
那么,$G'$ 至少有一个连通块不包含顶点 $v_i$,若那个连通块包含的边至少有一条边权为 $0$,那么矩阵 $(B_i)_{[|V|-1],S}$ 中必然有一列元素全为 $0$,否则将那个连通块包含的所有边对应的列在矩阵 $(B_i)_{[|V|-1],S}$ 中乘以特定比例(不为 $0$)再累加,一定可以得到一列元素全部为 $0$,此时一定有 $\det((B_i)_{[|V|-1],S})=0$。
若无向图 $G$ 的生成子图 $G'=(V,E')$ 是图 $G$ 的生成树,那么将树 $G'$ 视为有根树,设顶点 $v_i$ 为根。
将顶点按树上的不带权深度从小到大排序排序,除去根外从前到后枚举。
设当前考虑的顶点为 $v_j$,容易看出该顶点向其父亲连的边所对应的列只有该顶点对应的行的元素可能不为 $0$。若为 $0$,则 $\text{weight}(G')=\det((B_i)_{[|V|-1],S})^2=0$,否则,将该列的若干倍向该顶点向其儿子连的边所对应的列相加,使该节点向其儿子连的边对应的列其中该节点对应的行的元素为 $0$。
最后得到每列均有恰好一个非零元素的矩阵,行列式不变。
那么有 $\displaystyle\det((B_i)_{[|V|-1],S})=\sqrt{\prod_{e_j\in E'}w_j}$ 或 $\displaystyle\det((B_i)_{[|V|-1],S})=-\sqrt{\prod_{e_j\in E'}w_j}$,则 $\displaystyle\det((B_i)_{[|V|-1],S})^2=\prod_{e_j\in E'}w_j=\text{weight}(G')$。
那么 $\det(M(L)_{i,i})$ 就等于 $G$ 所有生成树 $T_G$ 的权值和。
## 证明矩阵树定理二
对于有向图 $G=(V,E)$,其出度 Laplace 矩阵为矩阵 $L^{\text{out}}$,其入度 Laplace 矩阵为矩阵 $L^{\text{in}}$。
构造 $|V|\times|E|$ 矩阵 $C$ 的方式如下:
$$
C_{i,j}=\left\{\begin{matrix}\sqrt{w_j}&i=x_j\\-\sqrt{w_j}&i=y_j\\0&i\ne x_j\wedge i\ne y_j\end{matrix}\right.
$$
构造 $|V|\times|E|$ 矩阵 $C^{\text{out}}$ 的方式如下:
$$
(C^{\text{out}})_{i,j}=\left\{\begin{matrix}\sqrt{w_j}&i=x_j\\0&i\ne x_j\end{matrix}\right.
$$
构造 $|V|\times|E|$ 矩阵 $C^{\text{in}}$ 的方式如下:
$$
(C^{\text{in}})_{i,j}=\left\{\begin{matrix}-\sqrt{w_j}&i=y_j\\0&i\ne y_j\end{matrix}\right.
$$
设 $M^{\text{out}}=C^{\text{out}}C^{T}$,根据矩阵乘法的定义,有 $M^{\text{out}}$ 为 $|V|$ 阶方阵,$\displaystyle(M^{\text{out}})_{i,j}=\sum_{k=1}^{|E|}(C^{\text{out}})_{i,k}(C^{T})_{k,j}=\sum_{k=1}^{|E|}(C^{\text{out}})_{i,k}C_{j,k}$。
当 $i=j$ 时,有:
$$
\begin{aligned}&(M^{\text{out}})_{i,j}\\=&(M^{\text{out}})_{i,i}\\=&\sum_{k=1}^{|E|}(C^{\text{out}})_{i,k}C_{i,k}\\=&\sum_{k=1}^{|E|}w_{k}[i=x_k]\\=&(L^{\text{out}})_{i,i}\end{aligned}
$$
当 $i\ne j$ 时,有:
$$
\begin{aligned}&(M^{\text{out}})_{i,j}\\=&\sum_{k=1}^{|E|}(C^{\text{out}})_{i,k}C_{j,k}\\=&\sum_{k=1}^{|E|}-w_{k}[i=x_k\wedge j=y_k]\\=&(L^{\text{out}})_{i,j}\end{aligned}
$$
那么 $C^{\text{out}}C^{T}=L^{\text{out}}$。
设 $M^{\text{in}}=C(C^{\text{in}})^{T}$,根据矩阵乘法的定义,有 $M^{\text{in}}$ 为 $|V|$ 阶方阵,$\displaystyle(M^{\text{in}})_{i,j}=\sum_{k=1}^{|E|}C_{i,k}((C^{\text{in}})^{T})_{k,j}=\sum_{k=1}^{|E|}C_{i,k}(C^{\text{in}})_{j,k}$。
当 $i=j$ 时,有:
$$
\begin{aligned}&(M^{\text{in}})_{i,j}\\=&(M^{\text{in}})_{i,i}\\=&\sum_{k=1}^{|E|}C_{i,k}(C^{\text{in}})_{i,k}\\=&\sum_{k=1}^{|E|}w_{k}[i=y_k]\\=&(L^{\text{in}})_{i,i}\end{aligned}
$$
当 $i\ne j$ 时,有:
$$
\begin{aligned}&(M^{\text{in}})_{i,j}\\=&\sum_{k=1}^{|E|}C_{i,k}(C^{\text{in}})_{j,k}\\=&\sum_{k=1}^{|E|}-w_{k}[i=x_k\wedge j=y_k]\\=&(L^{\text{in}})_{i,j}\end{aligned}
$$
那么 $C(C^{\text{in}})^{T}=L^{\text{in}}$。
设矩阵 $B_i=C_{[|V|]-\{i\},[|E|]}$,$B^{\text{out}}_i=(C^{\text{out}})_{[|V|]-\{i\},[|E|]}$,$B^{\text{in}}_i=(C^{\text{in}})_{[|V|]-\{i\},[|E|]}$。
不难证明 $B^{\text{out}}_i(B_i)^{T}=M(L^{\text{out}})_{i,i}$,$B_i(B^{\text{in}}_i)^{T}=M(L^{\text{in}})_{i,i}$。
那么根据柯西-比内公式,有:
$$
\begin{aligned}&\det(M(L^{\text{out}})_{i,i})\\=&\det(B^{\text{out}}_i(B_i)^{T})\\=&\sum_{|S|=|V|-1\wedge S\subseteq[|E|]}\det((B^{\text{out}}_i)_{[|V|-1],S})\det(((B_i)^{T})_{S,[|V|-1]})\\=&\sum_{|S|=|V|-1\wedge S\subseteq[|E|]}\det((B^{\text{out}}_i)_{[|V|-1],S})\det((B_i)_{[|V|-1],S})\end{aligned}
$$
考虑当 $|S|=|V|-1$ 且 $S\subseteq[|E|]$ 时 $\det((B^{\text{out}}_i)_{[|V|-1],S})\det((B_i)_{[|V|-1],S})$ 的意义。
不难想到,集合 $S$ 的意义就是从 $|E|$ 条边中选出 $|V|-1$ 条边,记选出的边集为 $E'=\{e_j\in E|j\in S\}$。
不难证明,有向图 $G=(V,E)$ 的生成子图 $G'=(V,E')$ 是以 $i$ 为根的内向生成树当且仅当 $|E'|=|V|-1$,且对于所有不超过 $|V|$ 的正整数 $j\ne i$,有一条边 $e_k\in E'$ 使得 $x_k=j$,且 $G'$ 中没有环。
若图 $G'=(V,E')$ 不是以 $i$ 为根的内向生成树,那么:
1. 若存在一个不超过 $|V|$ 的正整数 $j\ne i$,使得没有边 $e_k\in E'$ 使得 $x_k=j$,那么在矩阵 $(B^{\text{out}}_i)_{[|V|-1],S}$ 中顶点 $v_j$ 对应的一行元素全为 $0$,则 $\det((B^{\text{out}}_i)_{[|V|-1],S})=0$。
2. 否则,图 $G'$ 中存在环,若环上有至少一条边的边权为 $0$,那么在矩阵 $(B_i)_{[|V|-1],S}$ 中必然有一列元素全为 $0$,否则将环上的边在 $(B_i)_{[|V|-1],S}$ 中对应的列全部乘以特定比例(不为 $0$)再累加,一定可以得到一列元素全为 $0$,此时一定有 $\det((B_i)_{[|V|-1],S})=0$。
接下来假设图 $G'=(V,E')$ 是以 $i$ 为根的内向生成树。
不难看出,矩阵 $(B^{\text{out}}_i)_{[|V|-1],S}$ 每行每列都至多只有一个非零元素。
将顶点按树上的不带权深度从小到大排序排序,除去根外从前到后枚举。
设当前考虑的顶点为 $v_j$,容易看出该顶点与其父亲间连的边在矩阵 $(B_i)_{[|V|-1],S}$ 所对应的列只有该顶点对应的行的元素可能不为 $0$。若为 $0$,则 $\text{weight}(G')=\det((B^{\text{out}}_i)_{[|V|-1],S})\det((B_i)_{[|V|-1],S})=0$,否则,将该列的若干倍向该顶点与其儿子间连的边所对应的列相加,使该节点与其儿子间连的边在矩阵 $(B_i)_{[|V|-1],S}$ 对应的列其中该节点对应的行的元素为 $0$。
最后在行列式不变的前提下一定可以将 $(B_i)_{[|V|-1],S}$ 转化为 $(B^{\text{out}}_i)_{[|V|-1],S}$。
显然有 $\displaystyle\det((B^{\text{out}}_i)_{[|V|-1],S})=\sqrt{\prod_{e_j\in E'}w_j}$ 或 $\displaystyle\det((B^{\text{out}}_i)_{[|V|-1],S})=-\sqrt{\prod_{e_j\in E'}w_j}$,那么 $\displaystyle\det((B^{\text{out}}_i)_{[|V|-1],S})\det((B_i)_{[|V|-1],S})=\det((B^{\text{out}}_i)_{[|V|-1],S})^2=\prod_{e_j\in E'}w_j=\text{weight}(G')$。
那么 $\det(M(L^{\text{out}})_{i,i})$ 就等于 $G$ 所有以 $v_i$ 为根的内向生成树 $T'_G(v_i)$ 的权值和。
根据柯西-比内公式,还有:
$$
\begin{aligned}&\det(M(L^{\text{in}})_{i,i})\\=&\det(B_i(B^{\text{in}}_i)^{T})\\=&\sum_{|S|=|V|-1\wedge S\subseteq[|E|]}\det((B_i)_{[|V|-1],S})\det(((B^{\text{in}}_i)^{T})_{S,[|V|-1]})\\=&\sum_{|S|=|V|-1\wedge S\subseteq[|E|]}\det((B_i)_{[|V|-1],S})\det((B^{\text{in}}_i)_{[|V|-1],S})\end{aligned}
$$
考虑当 $|S|=|V|-1$ 且 $S\subseteq[|E|]$ 时 $\det((B_i)_{[|V|-1],S})\det((B^{\text{in}}_i)_{[|V|-1],S})$ 的意义。
不难想到,集合 $S$ 的意义就是从 $|E|$ 条边中选出 $|V|-1$ 条边,记选出的边集为 $E'=\{e_j\in E|j\in S\}$。
不难证明,有向图 $G=(V,E)$ 的生成子图 $G'=(V,E')$ 是以 $i$ 为根的外向生成树当且仅当 $|E'|=|V|-1$,且对于所有不超过 $|V|$ 的正整数 $j\ne i$,有一条边 $e_k\in E'$ 使得 $y_k=j$,且 $G'$ 中没有环。
若图 $G'=(V,E')$ 不是以 $i$ 为根的外向生成树,那么:
1. 若存在一个不超过 $|V|$ 的正整数 $j\ne i$,使得没有边 $e_k\in E'$ 使得 $y_k=j$,那么在矩阵 $(B^{\text{in}}_i)_{[|V|-1],S}$ 中顶点 $v_j$ 对应的一行元素全为 $0$,则 $\det((B^{\text{in}}_i)_{[|V|-1],S})=0$。
2. 否则,图 $G'$ 中存在环,若环上有至少一条边的边权为 $0$,那么在矩阵 $(B_i)_{[|V|-1],S}$ 中必然有一列元素全为 $0$,否则将环上的边在 $(B_i)_{[|V|-1],S}$ 中对应的列全部乘以特定比例(不为 $0$)再累加,一定可以得到一列元素全为 $0$,此时一定有 $\det((B_i)_{[|V|-1],S})=0$。
接下来假设图 $G'=(V,E')$ 是以 $i$ 为根的外向生成树。
不难看出,矩阵 $(B^{\text{in}}_i)_{[|V|-1],S}$ 每行每列都至多只有一个非零元素。
将顶点按树上的不带权深度从小到大排序排序,除去根外从前到后枚举。
设当前考虑的顶点为 $v_j$,容易看出该顶点与其父亲间连的边在矩阵 $(B_i)_{[|V|-1],S}$ 所对应的列只有该顶点对应的行的元素可能不为 $0$。若为 $0$,则 $\text{weight}(G')=\det((B_i)_{[|V|-1],S})\det((B^{\text{in}}_i)_{[|V|-1],S})=0$,否则,将该列的若干倍向该顶点与其儿子间连的边所对应的列相加,使该节点与其儿子间连的边在矩阵 $(B_i)_{[|V|-1],S}$ 对应的列其中该节点对应的行的元素为 $0$。
最后在行列式不变的前提下一定可以将 $(B_i)_{[|V|-1],S}$ 转化为 $(B^{\text{in}}_i)_{[|V|-1],S}$。
显然有 $\displaystyle\det((B^{\text{in}}_i)_{[|V|-1],S})=\sqrt{\prod_{e_j\in E'}w_j}$ 或 $\displaystyle\det((B^{\text{in}}_i)_{[|V|-1],S})=-\sqrt{\prod_{e_j\in E'}w_j}$,那么 $\displaystyle\det((B_i)_{[|V|-1],S})\det((B^{\text{in}}_i)_{[|V|-1],S})=\det((B^{\text{in}}_i)_{[|V|-1],S})^2=\prod_{e_j\in E'}w_j=\text{weight}(G')$。
那么 $\det(M(L^{\text{in}})_{i,i})$ 就等于 $G$ 所有以 $v_i$ 为根的外向生成树 $T^{*}_G(v_i)$ 的权值和。
# 闲话
居然一不小心水了 $23000+$ 字符,之前开始写的时候根本没想到。
感觉有很多地方写得都不是很好,~~有些地方还自由发挥~~不过写完了也是感觉很开心。
既然都看到这里了,就做几道习题吧。(题目来源为洛谷与 AtCoder)
[【模板】Matrix-Tree 定理](https://www.luogu.com.cn/problem/P6178)(模板)
[[SDOI2014] 重建](https://www.luogu.com.cn/problem/P3317)(板题)
[[SHOI2016] 黑暗前的幻想乡](https://www.luogu.com.cn/problem/P4336)(与容斥结合)
[[省选联考 2020 A 卷] 作业题](https://www.luogu.com.cn/problem/P6624)(与[莫比乌斯反演](https://oi.wiki/math/number-theory/mobius/)结合)
[Inversion of Tree](https://atcoder.jp/contests/abc323/tasks/abc323_g)(矩阵树定理的特征值表述形式,具体可见 [OI Wiki](https://oi.wiki/graph/matrix-tree/#%E5%AE%9A%E7%90%86%E5%8F%99%E8%BF%B0))
[Spanning Trees of Interval Graph](https://atcoder.jp/contests/agc060/tasks/agc060_f)(与矩阵行列式引理(Matrix determinant lemma)结合,具体可百度)
[Select and Split](https://atcoder.jp/contests/arc173/tasks/arc173_f)(需要将问题转化)