\color{#3498db}\bf[upd2021.03.19]

Part -999 感谢列表

（排名不分先后）

• 计算几何「OI-Wiki」
• 数论小白都能看懂的平面凸包详解 「ShineEternal的博客」
• 几何画图「GeoGebra」 离线版
• 感谢@rui_er 指出了一个错误
• 感谢@MicroMaker hack，指出了错误

Part 1 前言

限于笔者能力有限，本学习笔记如有错误，并非有意，非常欢迎指出。

$\color{#3498db}\footnotesize\bf[upd2021.03.21]$ $\footnotesize\color{red}\textsf{\textbf{作者在 Firefox，Chrome，Edge 均已测试图片无任何问题。}}

Part 2 何为计算几何

学二维凸包，我们首先需要了解的就是计算几何。

计算几何，就是利用计算机建立数学模型解决几何问题。

要用电脑解几何题？数学好的同学们笑了。

我们并不是用计算机算数学卷子上的几何题去了，而是解决一些更加复杂的几何相关问题。

为了解决复杂且抽象的问题，我们一定要选择合适的研究方法。对于计算机来说，给它看几何图形……

Part 3 二维凸包

Part 3.1 凸多边形

凸多边形是指所有内角大小都在 [0, \pi] 范围内的 简单多边形 。

Part 3.2 凸包

「

在平面上能包含所有给定点的最小凸多边形叫做凸包。

其定义为：对于给定集合 X ，所有包含 X 的凸集的交集 S 被称为 X 的 凸包 。

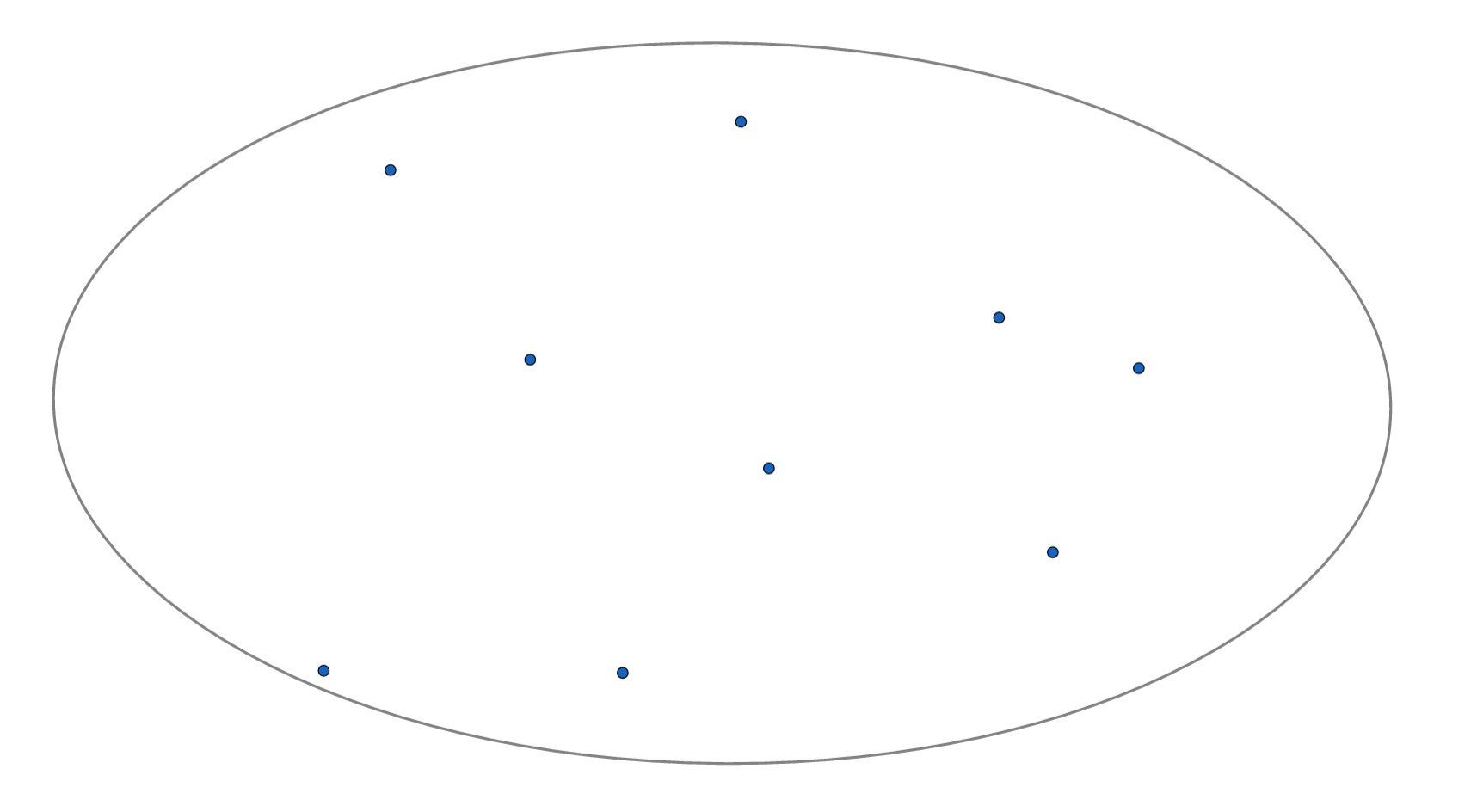
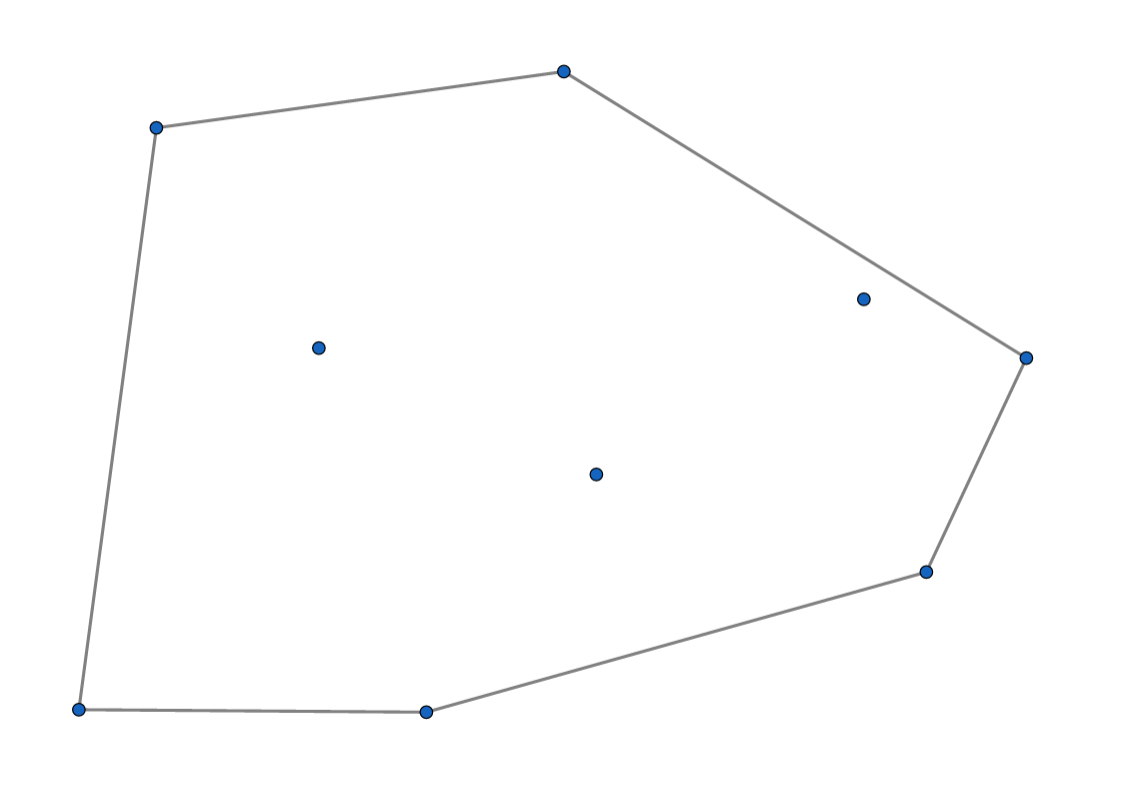
」 其实我们可以把凸包看成一个拿橡皮筋围成的一个图形。 假设有一个布满小凸起的板子：  我们要把这些凸起都围起来，怎么围呢？ 显然，最简单方便的方法是这样：  但是，我们知道，橡皮筋是有弹力的，所以橡皮筋会往里缩，直到这样：  最外圈的凸起撑起了橡皮筋。 此时橡皮筋围成的多边形的顶点就是最外圈凸起所在的位置。 由此，我们就定义橡皮筋围成的图形为一个平面凸包。 那么，换一种定义，就为： **平面凸包是指覆盖平面上 $n$ 个点的最小的凸多边形。** 当然，我们发现在程序中却无法模拟橡皮筋收缩的过程，于是有了下文的诞生。 ### Part 3.3 二维凸包的求法 在这里我们只讲两种主要的也是最常用的二维凸包的求法。 #### Part 3.3.1 Graham 算法 Graham 算法的本质： Graham 扫描算法维护一个凸壳，通过不断在凸壳中加入新的点和去除影响凸性的点，最后形成凸包。 凸壳：凸包的一部分。 此算法主要分为两部分： - 排序 - 扫描 ##### Part 3.3.1.1 排序 我们先选择一个 $y$ 最小的点（如 $y$ 相同选 $x$ 最小），记为 $p_1$。 剩下的点，按照极角的大小逆时针排序，记为 $p_2,p_3,\dots, p_m$。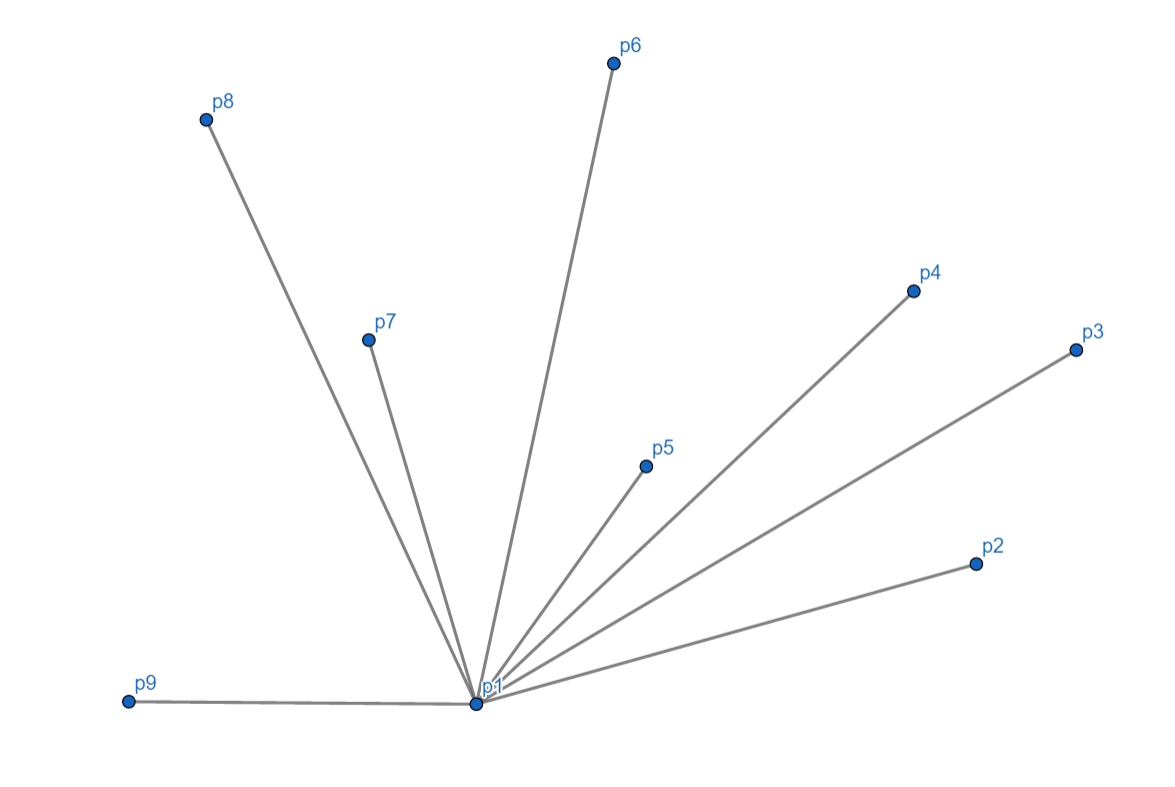  ##### Part 3.3.1.2 扫描 （下列所说的左右等是指以上一条连线为铅垂线，新的连线偏移的方向） 刚开始，我们的点集是这样的：  $p_1$ 为起始点。 随后，$p_2$ 准备入栈，由于栈元素很少，所以可以入栈。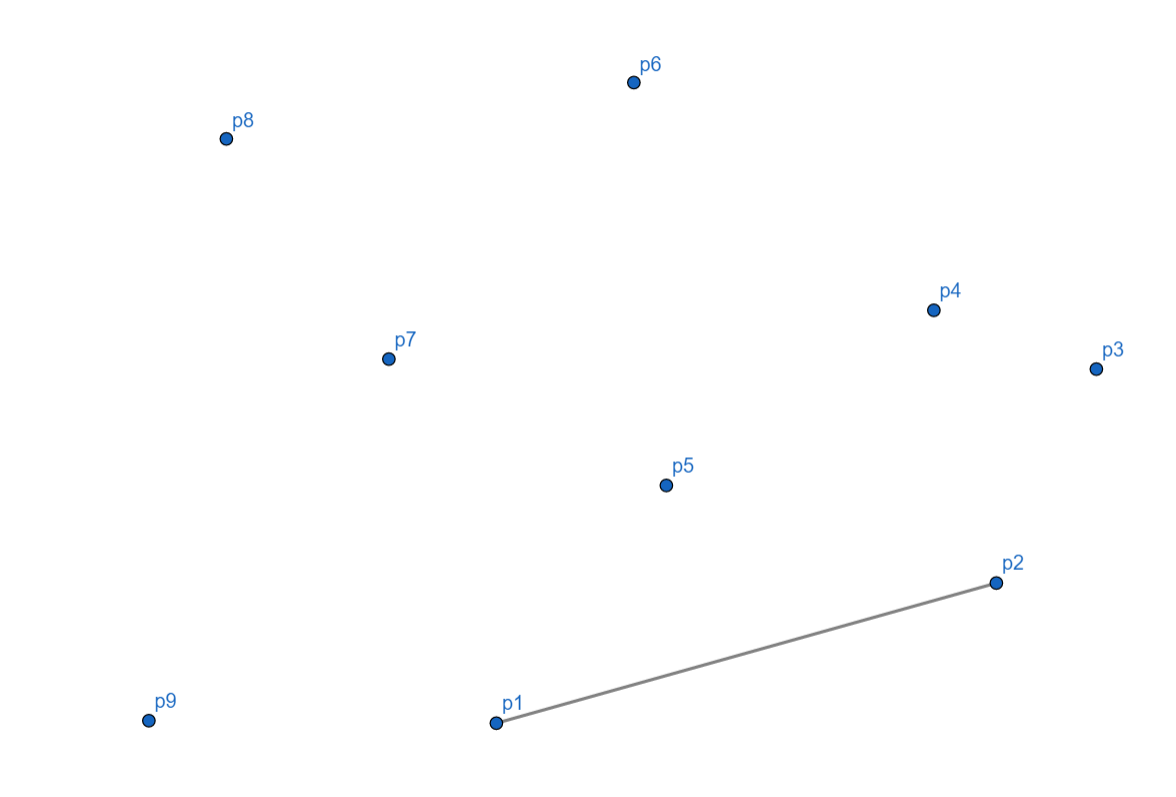  再看 $p_3$，因为 $p_3$ 向左，符合凸包条件，入栈。  随后 $p_4$ 也一切正常，依然向左，入栈。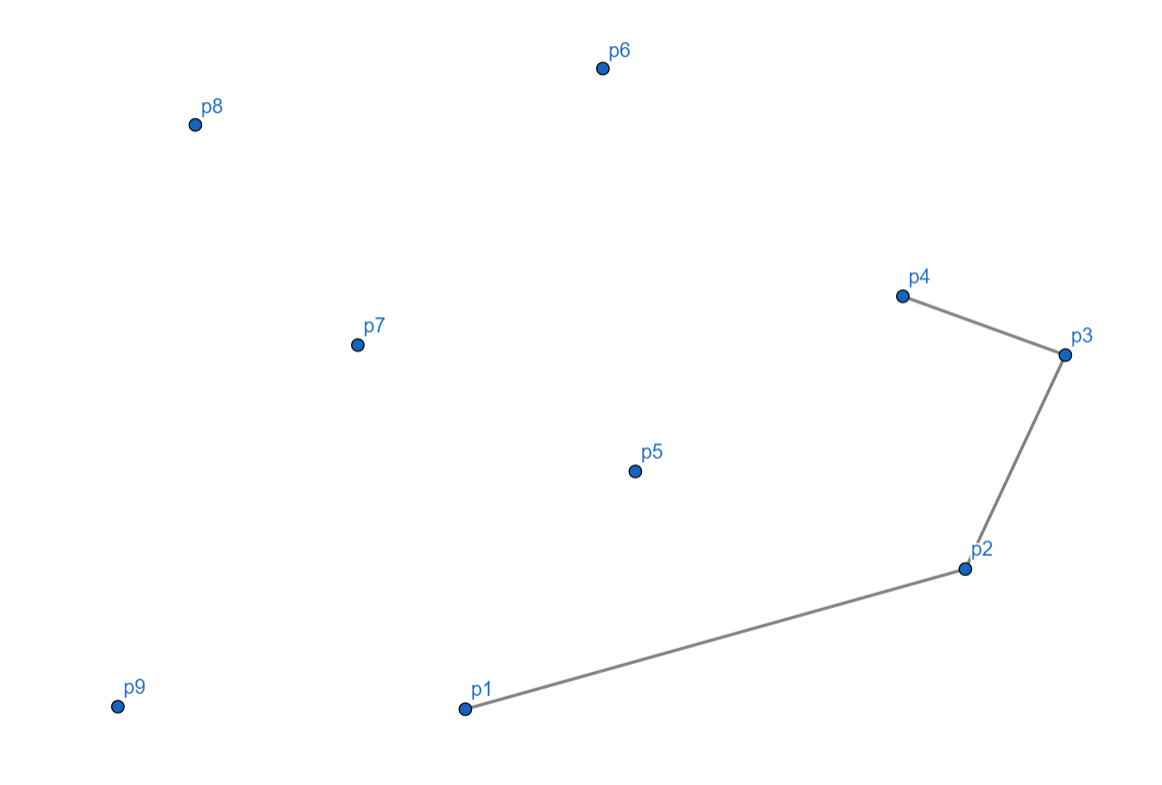  $p_5$ 依然向左，入栈。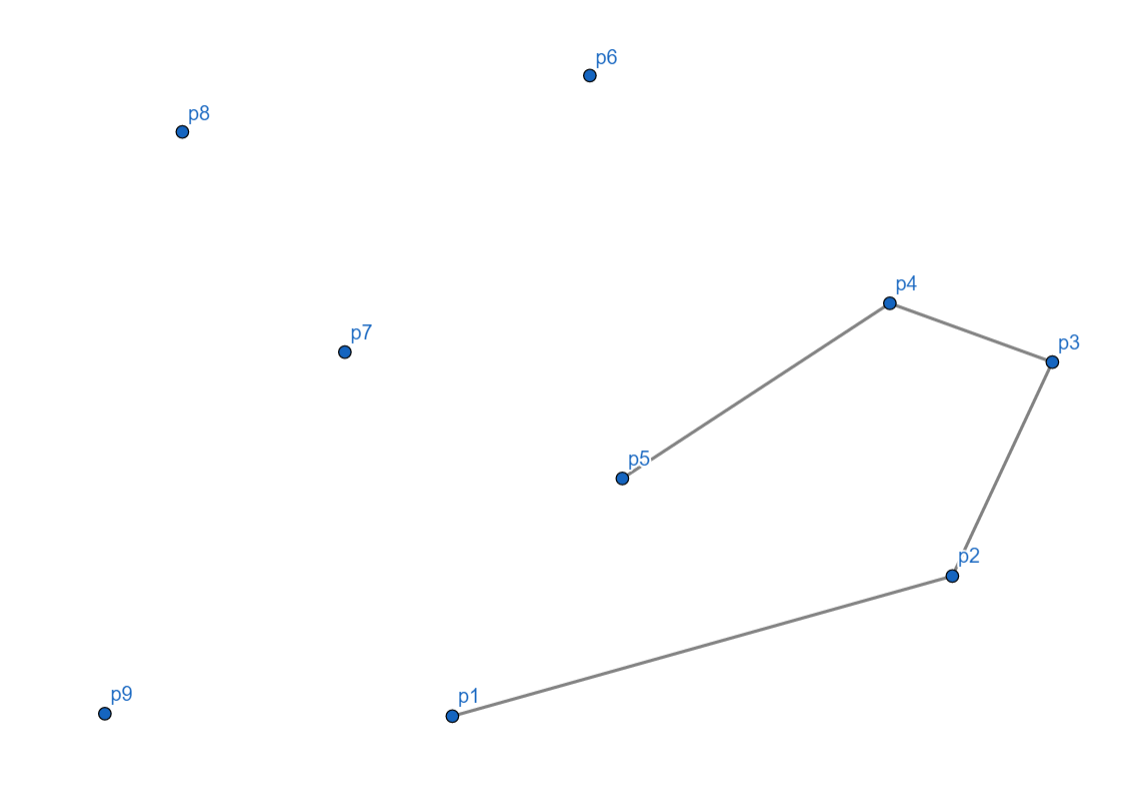  到 $p_6$ 时，我们发现了点问题，就是不再是向左了，而是向右了，所以我们此时要将 $p_5$ 出栈，$p_6$ 入栈。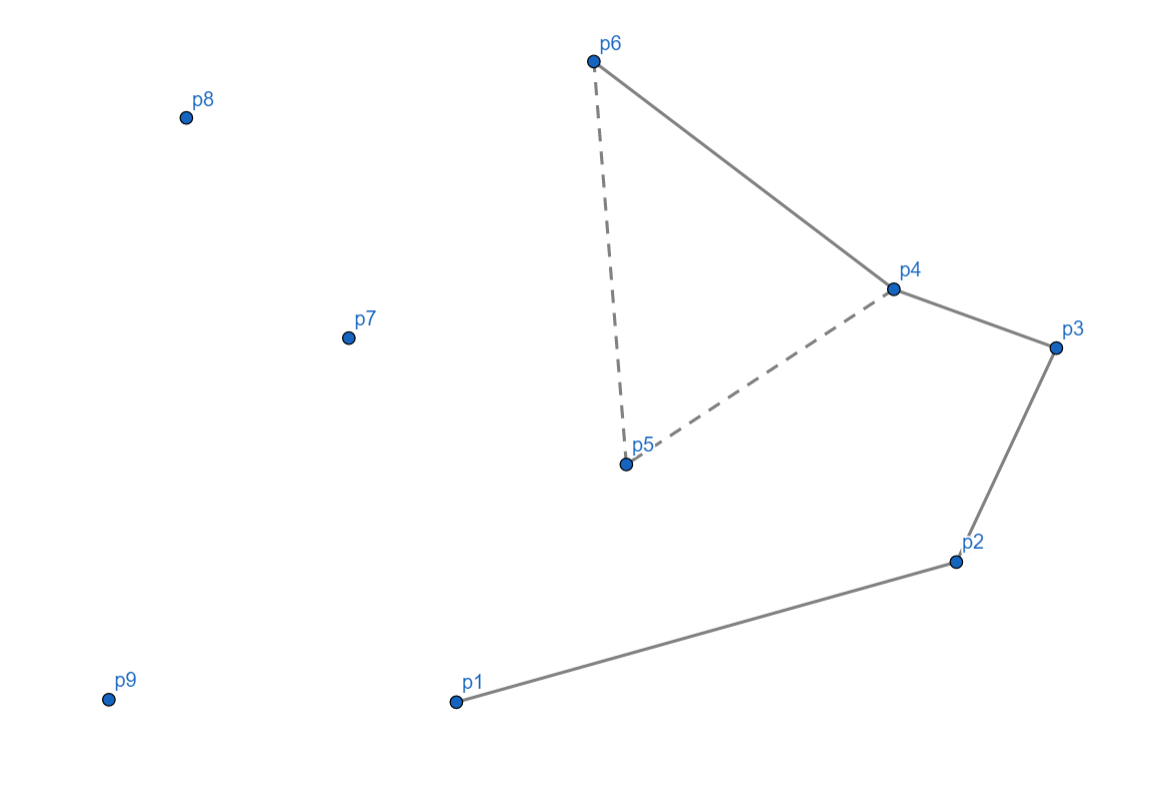  入栈后，我们发现，相对于 $p_4$，$p_6$ 依然是向右的，所以我们还要把 $p_4$ 出栈，$p_6$ 入栈。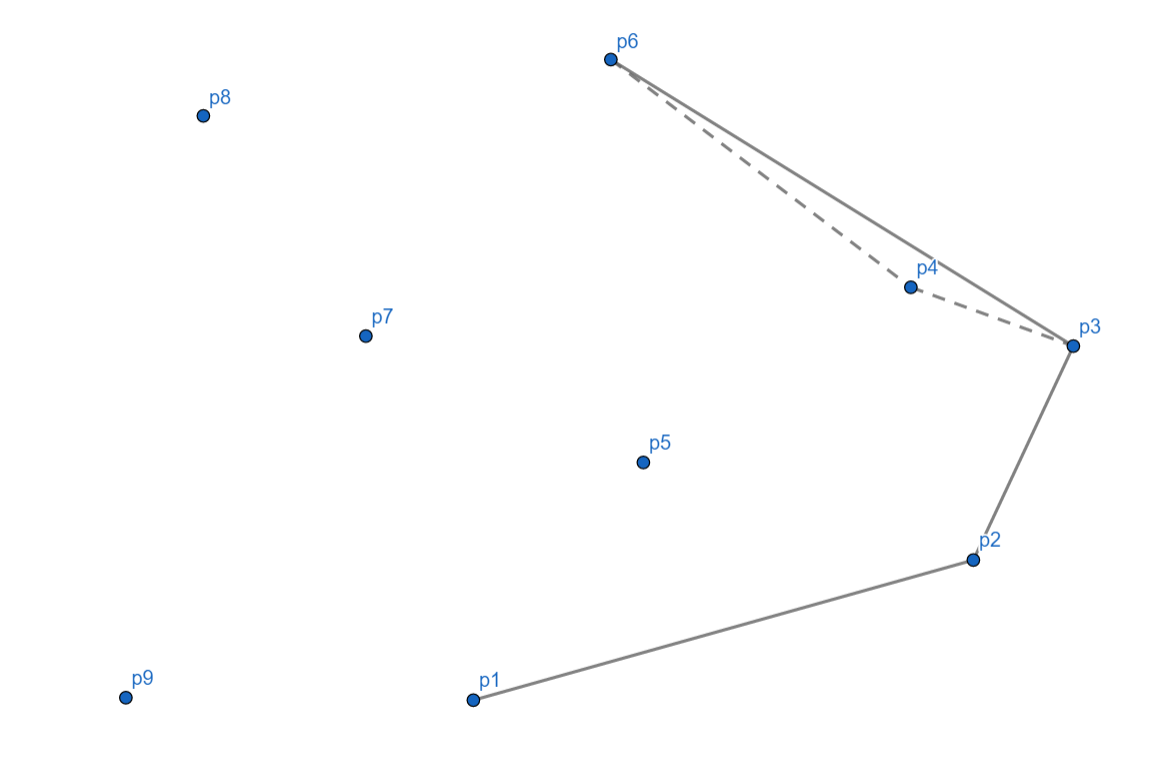  接下来 $p_7$ 没有问题。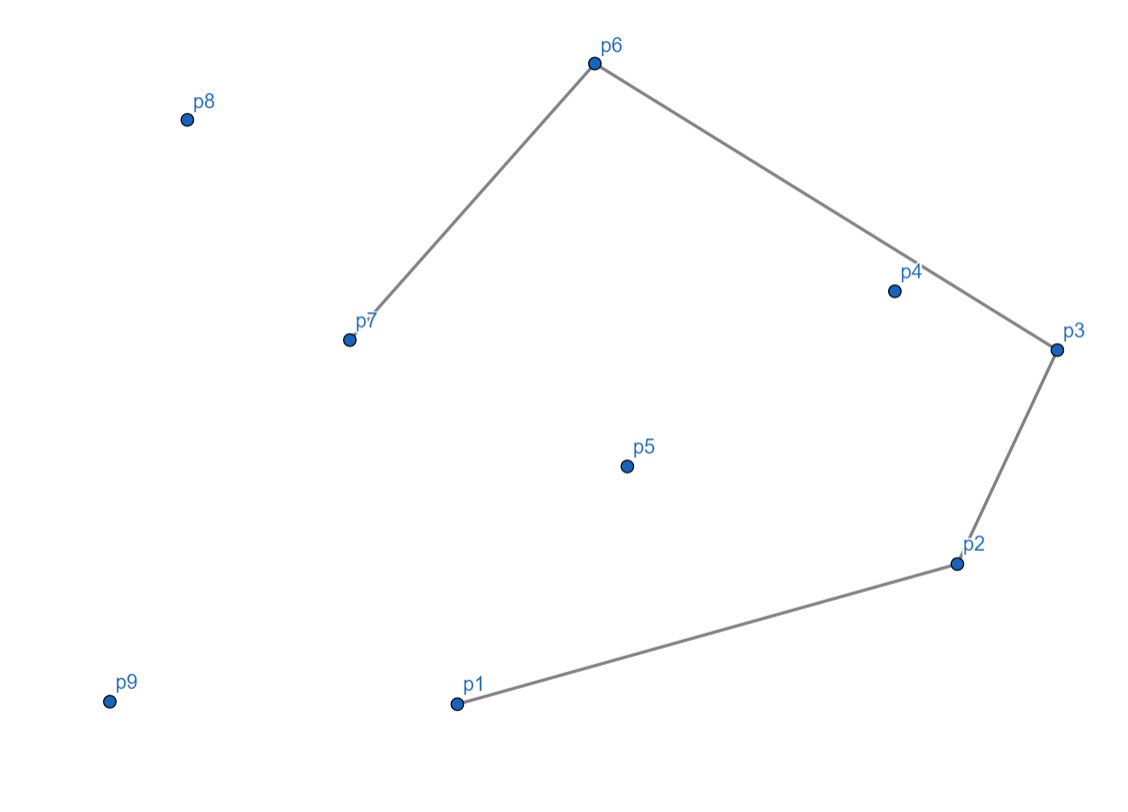  $p_8$ 时，我们发现，也是向右的，所以将 $p_7$ 出栈，$p_8$ 入栈。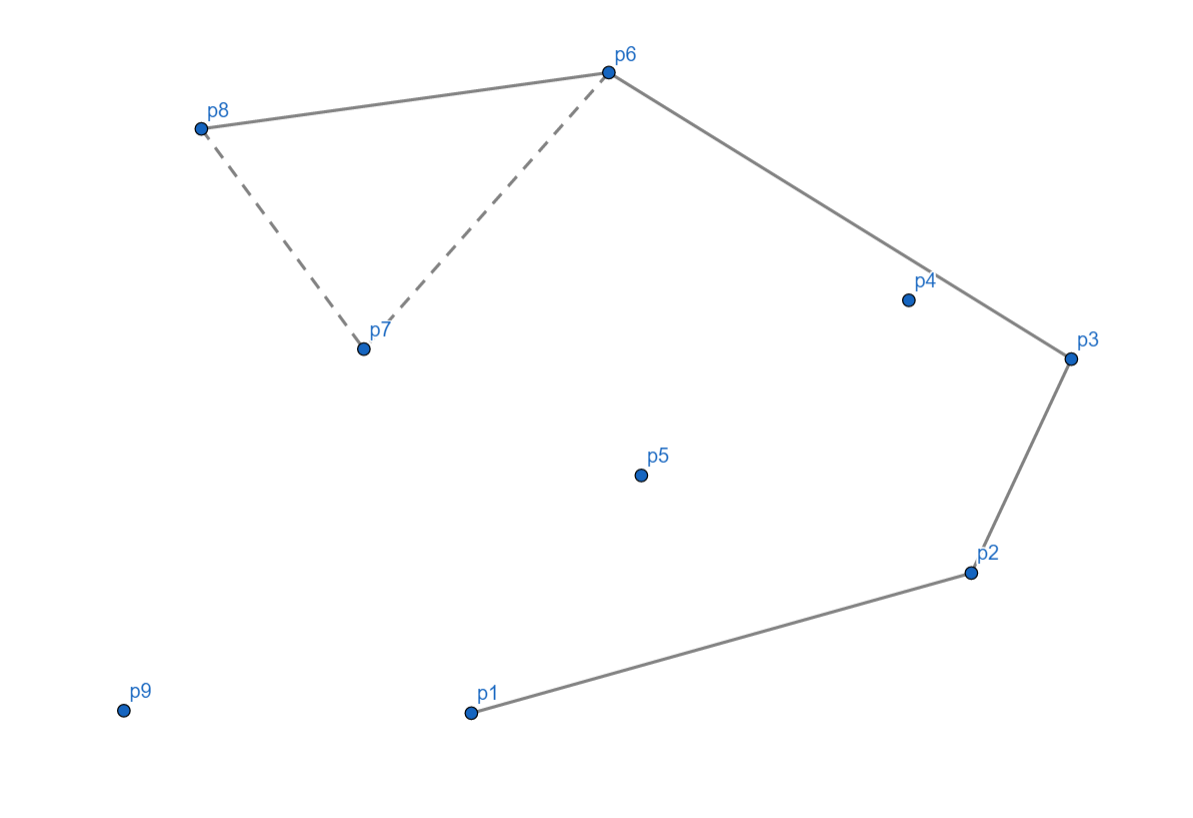  接下来 $p_9$ 正常，入栈。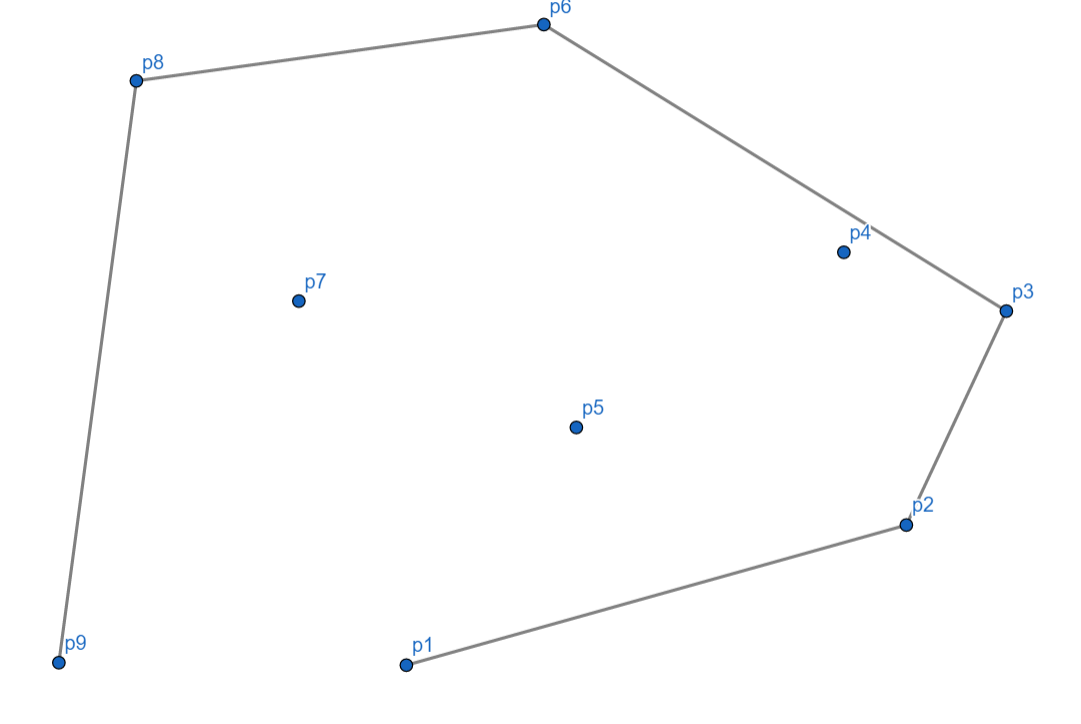  最后，我们再把最后一个点和第一个点连起来。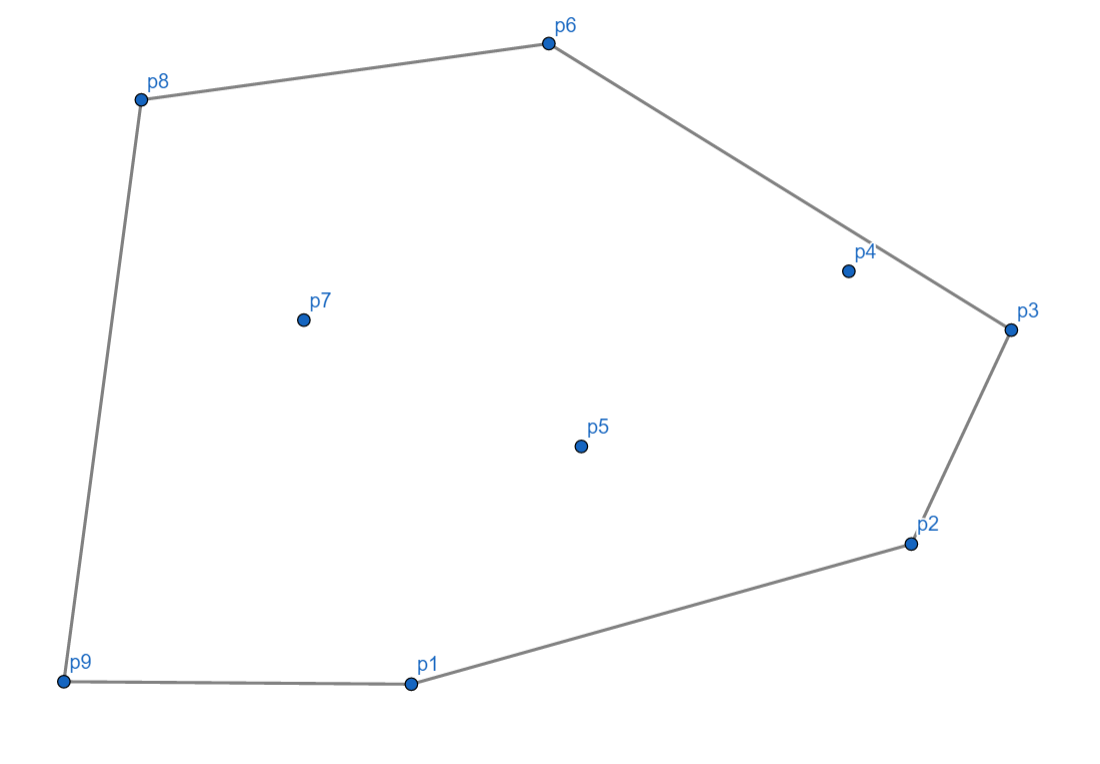  此时，我们的 Graham 算法的全过程就结束了。 时间复杂度为 $O(n \log n)$。 #### Part 3.3.2 Andrew 算法 Graham 算法的一种进阶。 假设我们有这些点：  首先把所有点以横坐标为第一关键字，纵坐标为第二关键字排序。  相对于 Graham 算法来说，Andrew 算法排序更简单，按 $x, y$ 坐标排序，时间复杂度也更低（一般的坐标系中排序方法）。 首先将 $p_1$ 入栈。 然后也将 $p_2$ 入栈，$p_2$ 可能在，也可能不在，等着之后判断。  随后，发现 $p_3$ 偏右，所以我们将 $p_2$ 出栈。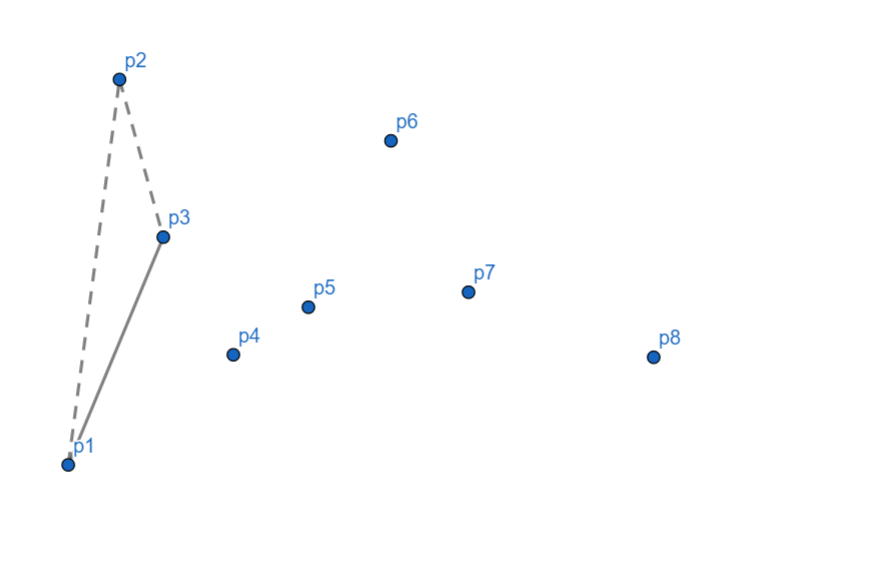  发现 $p_4$ 依然偏右，$p_3$ 出栈，$p_4$ 入栈。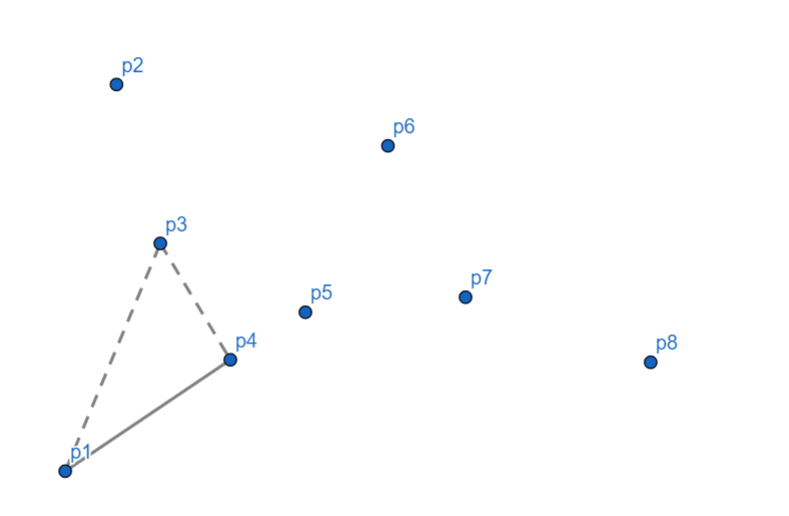  $p_5$ 向右，$p_4$ 出栈，$p_5$ 入栈。  $p_6$ 向左，入栈。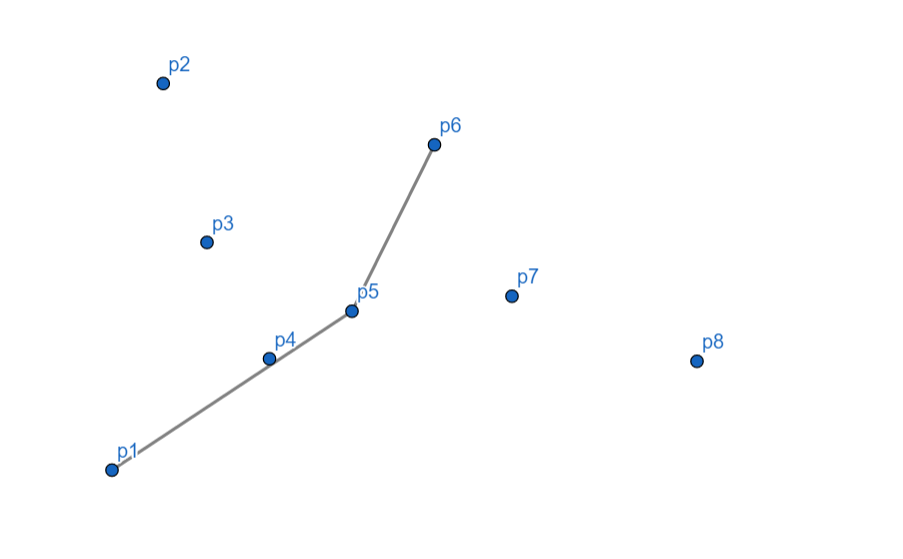  $p_7$ 向右，$p_6$ 出栈，$p_7$ 入栈。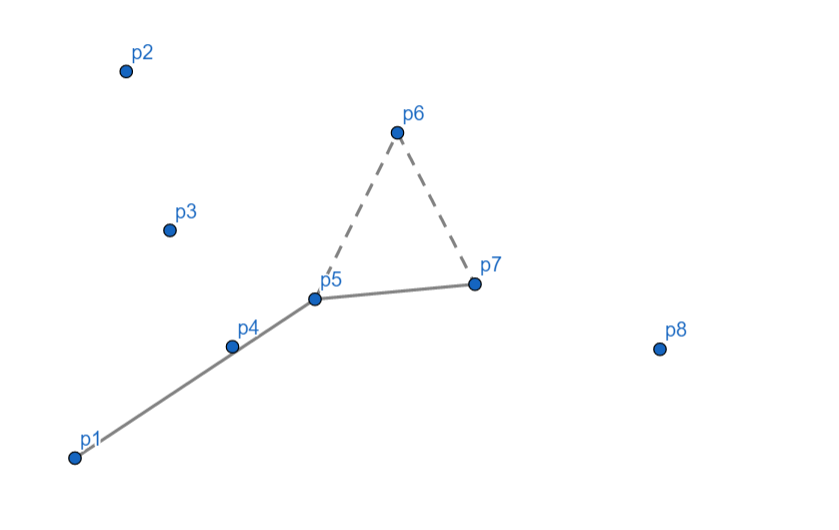  $p_8$ 向右，$p_7$ 出栈，继续检查发现相对于 $p_5$ $p_8$ 仍然向右，$p_5$ 出栈，$p_8$ 入栈。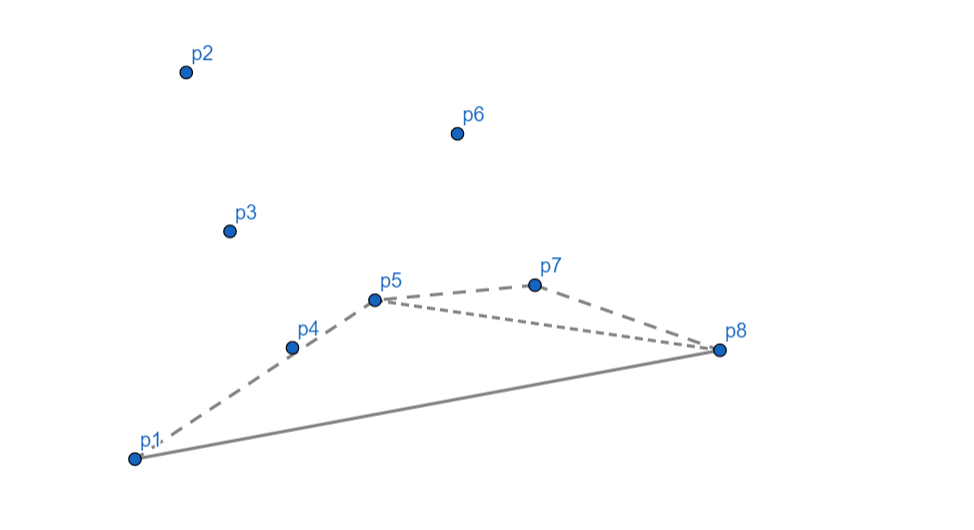  此时，我们发现，凸包空了一半。 所以我们需要再从排序末尾的点（也就是 $p_8$）出发，按照一模一样的方式再算一遍就行了。 当然如果我们走过的点就不许要再走了（除了 $p_1$）. 从 $p_8$ 到 $p_7$，向左，$p_7$ 入栈。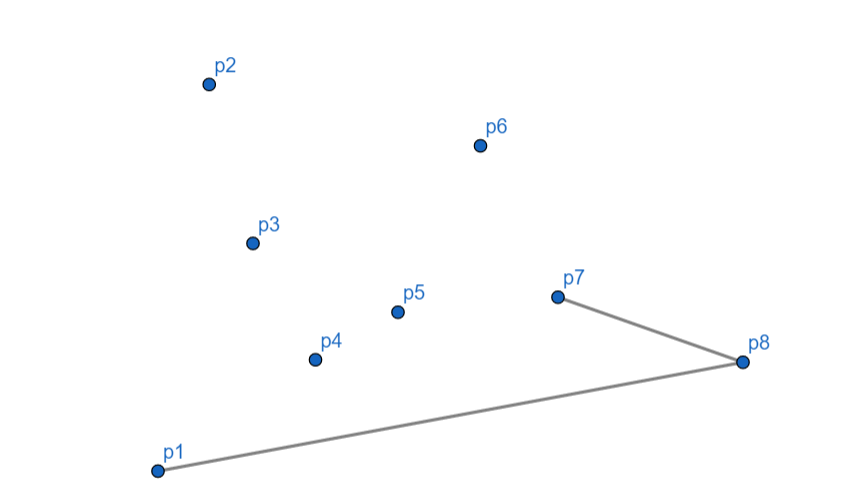  $p_6$ 向右，$p_7$ 出栈，$p_6$ 入栈。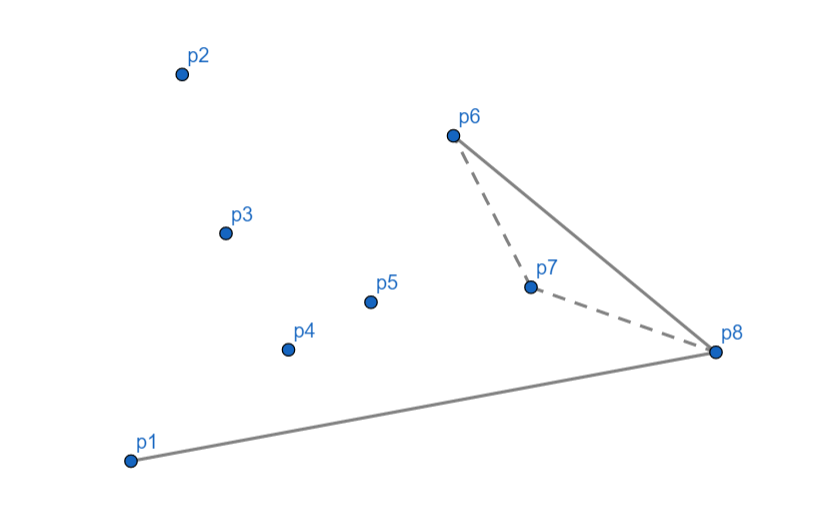  $p_5$ 向左，入栈。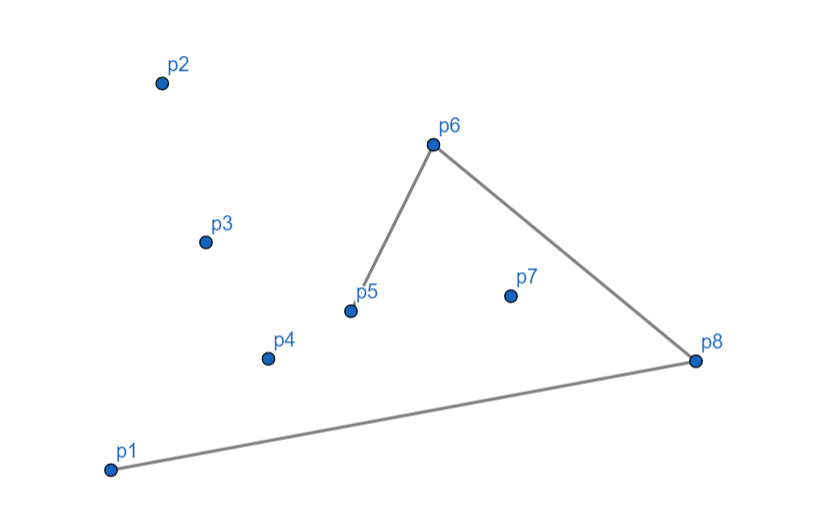  $p_4$ 向左，入栈。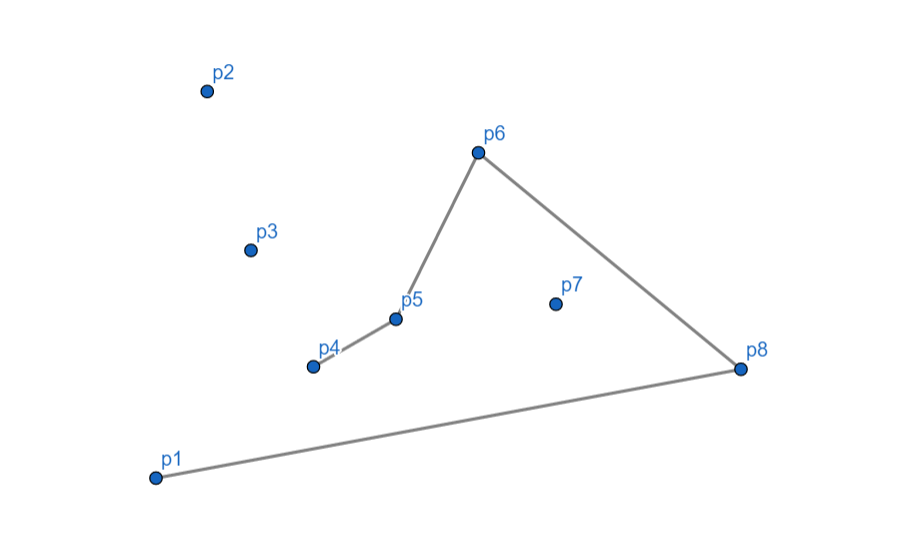  $p_3$ 向右，$p_4$ 出栈，对于 $p_5$ $p_3$ 依然向右，$p_5$ 出栈，$p_3$ 入栈。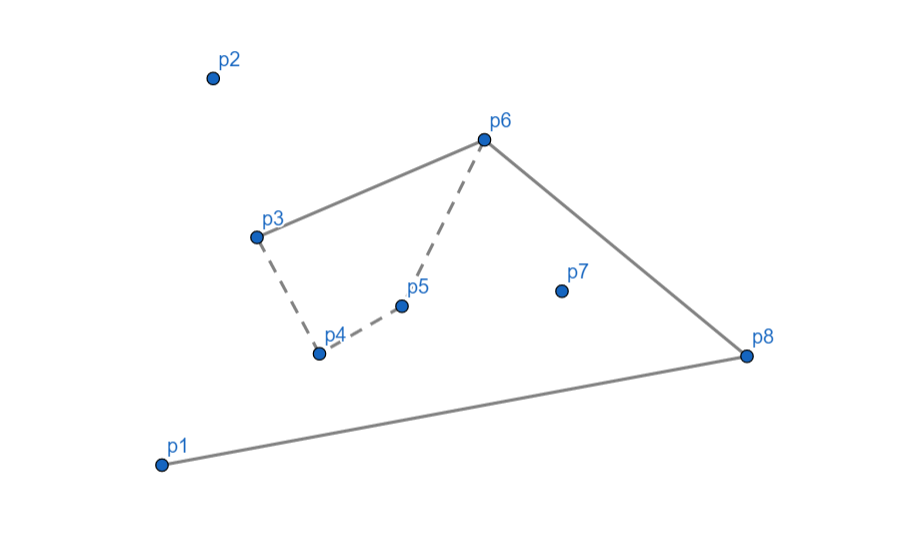  $p_2$ 向右，$p_3$ 出栈，$p_2$ 入栈。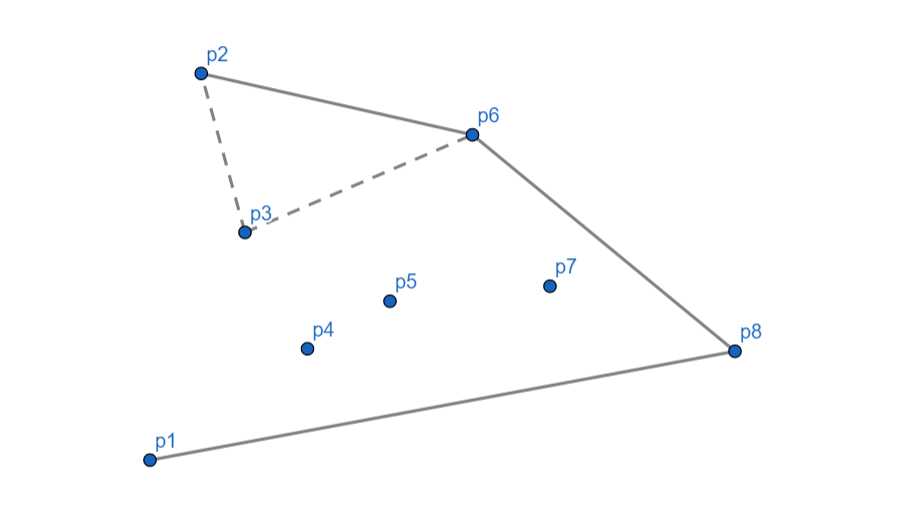  最后将 $p_2$ 和 $p_1$ 连起来。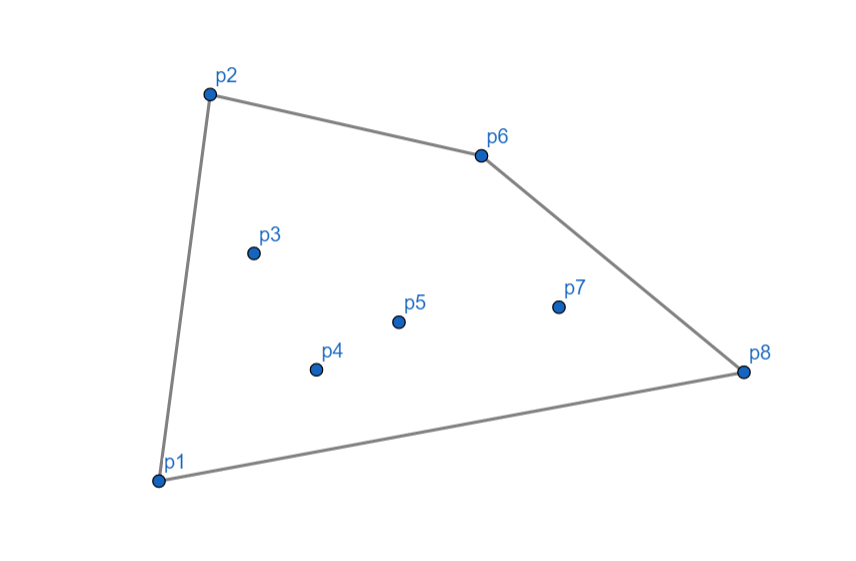  至此，我们的 Andrew 算法就完成了！ 时间复杂度：$O(n \log n)

Part 3.4 实战演练

Part 3.4.1 P2742 [USACO5.1]圈奶牛Fencing the Cows /【模板】二维凸包

先拿模板题练练手。

题目简述：求一个二维凸包的周长。

拿 Graham 算法做即可。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<string>
#define line cout << endl
using namespace std;
const int NR = 1e5 + 5;
int n;
double ans;
struct point {
    double x, y;
};
point p[NR], ps[NR];
double dis (point pa, point pb) { //求两点间距离
    return sqrt ((pb.x - pa.x) * (pb.x - pa.x) + (pb.y - pa.y) * (pb.y - pa.y));
}
double cp (point pa1, point pa2, point pb1, point pb2) { //求叉积
    return (pa2.x - pa1.x) * (pb2.y - pb1.y) - (pb2.x - pb1.x) * (pa2.y - pa1.y);
}
bool cmp (point px, point py) { //排序
    double num = cp (p[1], px, p[1], py);
    if (num > 0) return true;
    if (num == 0 && dis (p[0], px) < dis (p[0], py)) return true;
    return false;
}
int main () {
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> p[i].x >> p[i].y;
        if(i != 1 && p[i].y < p[1].y) { //去重
            swap (p[i].y, p[1].y);
            swap (p[i].x, p[1].x);
        }
    }
    sort (p + 2, p + n + 1, cmp);
    ps[1] = p[1]; //最低点是肯定在凸包里的
    int h = 1;
    for (int i = 2; i <= n; i++) {
        while (h > 1 && cp (ps[h - 1], ps[h], ps[h], p[i]) <= 0) { //判断是向左还是向右，如果向右就出栈
            h--;
        }
        h++;
        ps[h] = p[i];
    }
    ps[h + 1] = p[1]; //最后一个点跟第一个点相连
    for (int i = 1; i <= h; i++) {
        ans += dis (ps[i], ps[i + 1]); //累加
    }
    printf ("%.2lf\n", ans);
    return 0;
}

\color{#3498db}\footnotesize\bf[upd2021.03.19]

发现本代码被 hack 了？为什么？

我们分析，按照这种算法，那么在所有点都在一条线的时候就会出问题，无法回到起点，那么我们只需特判一下即可。

Part 3.4.2 UVA11626 Convex Hull

这题好像拿 Graham 会 TLE？拿 Andrew罢，也是道模板题。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<string>
#define line cout << endl
using namespace std;
const int NR = 1e5 + 5;
const double eps = 1e-7;
int n;
struct point {
    double x, y;
    point () {}
    point (double a, double b) : x (a), y (b) {}
    bool operator < (const point &b) const {
        if (x < b.x) return 1;
        if (x > b.x) return 0;
        return y < b.y;
    }
    point operator - (const point &b) {
        return point (x - b.x, y - b.y);
    }
};
point p[NR], sp[NR];
int cmp (double x) {
    if (fabs (x) < eps) return 0;
    return x > 0 ? 1 : -1;
}
double dis (point a, point b) {
    return sqrt ((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
}
double cp (point a, point b) {
    return a.x * b.y - a.y * b.x;
}
int Andrew () {
    sort (p + 1, p + 1 + n);
    int len = 0;
    for (int i = 1; i <= n; i++) {
        while (len > 1 && cmp (cp (sp[len] - sp[len - 1], p[i] - sp[len - 1])) < 0) 
            len--;
        sp[++len] = p[i];
    }
    int k = len;
    for (int i = n - 1; i >= 1; i--) {
        while (len > k && cmp (cp (sp[len] - sp[len - 1], p[i] - sp[len - 1])) < 0)
            len--;
        sp[++len] = p[i];
    }
    return len;
}
int main () {
    int t;
    cin >> t;
    while (t--) {
        cin >> n;
        char c;
        for (int i = 1; i <= n; i++)
            cin >> p[i].x >> p[i].y >> c;
        int t = Andrew();
        cout << t - 1 << endl;
        for (int i = 1; i < t; i++) 
            printf ("%.0lf %.0lf\n", sp[i].x, sp[i].y);
    }
    return 0;
}

The End...