[TOC]
ZROI
Day21: 状压 DP
状态压缩
状态是一个 k 进制数, 将每个元素的状态用每个 k 进制位的值表示.
轮廓线 DP
上一道题如果不是一行一起转移, 而是每个位置讨论放或者不放, 将讨论的状态变成这个位置及以上的一个轮廓线的状态, 这样可以优化时间复杂度, 从 O(2^nn) 状态, O(2^n) 转移优化到 O(2^nn^2) 状态, O(1) 转移.
SCOI2005
一个矩形, 分成 n * m 个格子, 有的格子能选, 有的不能选, 要求选择的格子两两不相邻, 求合法的选取方式数对 10^8 取模的余数.
设计状态 f_{i, j}, 表示从上到第 i 行, 第 i 行的状态是 j 的二进制表示的.
我们可以先预处理出合法的行状态, List_i 表示第 i 个没有两个格子相邻的行状态.
f_{i, j} = \sum_k^{k \in List, k \And j = k \And a_i = 0}(f_{i - 1, k})
注: a_i 是棋盘第 i 行状态.
但是因为一直以来想写 O(n^2(2^n)) 的做法, 所以趁机练习一下传说中的轮廓线 DP, 所以重新设计状态, 设 f_{i, j, k} 表示决策了 i - 1 行, 第 i 行决策到了第 j 列的合法方案数, 其中第 i 行的 [0, j] 列和第 i + 1 行的 [j + 1, m) 列拼起来的状态为 i.
状态数 O(n^2(2^n)) 转移可以做到 O(1), 复杂度 O, 本题 n = 12, 代入是 589824.
但是因为原来的做法复杂度和合法状态数 Cnt 有关, 所以原来 n(4^n) 的做法其实是 O(nCnt^2) 貌似也没有很劣, n = 12 时状态数是 377, 所以代入是 1705548, 因为原做法可以大量位运算优化, 并且没有那么多边界条件, 实际效率甚至比轮廓线优.
接下来放轮廓线代码:
const unsigned long long Mod(100000000);
unsigned long long f[15][15][4500], Ans;
unsigned a[15], m, n, n2, Cnt(0), A, B, C, D, t, Tmp(0);
int main() {
n = RD(), m = RD(), n2 = (1 << m);
for (register unsigned i(1); i <= n; ++i) {
for (register unsigned j(1); j <= m; ++j) {
a[i] <<= 1, a[i] += RD();
}
}
f[0][m - 1][0] = 1;
for (register unsigned i(1); i <= n; ++i) {
for (register unsigned k(0); k < n2; ++k) {
if(!(k & 1)) {f[i][0][k] = f[i - 1][m - 1][k ^ 1] + f[i - 1][m - 1][k]; if(f[i][0][k] >= Mod) f[i][0][k] -= Mod;}
if(a[i] & k & 1) f[i][0][k] = f[i - 1][m - 1][k ^ 1];
}
for (register unsigned j(1); j < m; ++j) {
for (register unsigned k(0); k < n2; ++k) {
if((k & (1 << j)) && (k & (1 << (j - 1)))) continue;
if(a[i] & k & (1 << j)) f[i][j][k] = f[i][j - 1][k ^ (1 << j)];
if(!(k & (1 << j))) {f[i][j][k] = f[i][j - 1][k ^ (1 << j)] + f[i][j - 1][k]; if(f[i][j][k] >= Mod) f[i][j][k] -= Mod;}
}
}
}
for (unsigned i(0); i < n2; ++i) Ans += f[n][m - 1][i];
printf("%llu\n", Ans % Mod);
return Wild_Donkey;
}
NOI2001
仍然先预处理出合法状态集合 List, 然后设计状态 f_{i, j, k} 表示算到第 i 行, 第 i 行状态为 j, 第 i - 1 行状态为 k 的情况.
f_{i, j, k} = \sum_{l}^{l \in List, l \And j = l \And k = l \And a_{i - 2} = 0} f_{i - 1, k, l}
早年诡异码风改了改, 细节不多不少, 枚举两排状态确实很神奇, 看起来非常慢, 实际上可行状态不多跑得飞快.
unsigned int a[105], f[105][65][65], List[65], m, n, N, Cnt(0), A, B, C, D, Ans(0);
bool b[10005];
char s;
inline unsigned int Gtnm(unsigned int x) {
unsigned int tmp(0);
while (x) {
if(x & 1) ++tmp;
x = x >> 1;
}
return tmp;
}
inline bool Judge (unsigned int x) {
unsigned int tmp(0x3f);
while (x) {
if(x & 1) {
if(tmp < 2) return 0;
tmp = 0;
}
else ++tmp;
x = x >> 1;
}
return 1;
}
int main() {
n = RD(), m = RD(), N = (1 << m) - 1;
for (register int i(0); i <= N; ++i) if (Judge(i)) List[++List[0]] = i;
for (register int i(1); i <= n; ++i) {
for (register int j(1); j <= m; ++j) {//init
while (s != 'H' && s != 'P') s = getchar();
a[i] = a[i] << 1;
if (s == 'H') ++a[i];
s = '0';
}
}
for (register unsigned int i(1); i <= List[0]; ++i) {//1st line
if (List[i] & a[1]) continue;//land
Cnt = Gtnm(List[i]);
f[1][i][1] = Cnt;
}
for (register unsigned int i(2); i <= n; ++i) {
for (register unsigned int j(1); j <= List[0]; ++j) {//this line
if (List[j] & a[i]) continue;//land
Cnt = Gtnm(List[j]);
for (register unsigned int k(1); k <= List[0]; ++k) {//last line
if(List[j] & List[k] || List[k] & a[i - 1]) continue;//Gun
for (register unsigned int l(1); l <= List[0]; ++l) {//last of last
if(List[j] & List[l] || List[k] & List[l] || List[l] & a[i - 2]) continue;
f[i][j][k] = max(f[i - 1][k][l] + Cnt, f[i][j][k]);
}
}
}
}
for (register unsigned int i(1); i <= List[0]; ++i)
for (register unsigned int j(1); j <= List[0]; ++j)
Ans = max(f[n][i][j], Ans);
printf("%u\n", Ans);
return Wild_Donkey;
}
SDOI2009
设计状态 f_{i, j, 0/1, k} 表示 i 前面都拿到饭, i 没拿到饭, j 集合的人已经拿到饭, 最后拿到饭的人是 i ± k 的最少时间.
f_{i, j, 0, k} = min(f_{i - k, (j << k) | (1 << (k - 1) - 1), 0, l} + (T_{i - k - l} \oplus T_{i - k}),\\
f_{i - k, (j << k) | (1 << (k - 1) - 1), 1, l} + (T_{i - k + l} \oplus T_{i - k}))\\
f_{i, j, 1, k} = min(f_{i, j - (1 << (k - 1)), 0, l} + (T_{i + k - l} \oplus T_{i + k}),\\
f_{i, j - (1 << (k - 1)), 1, l} + (T_{i + k + l} \oplus T_{i + k}))
注意这个题 i 拿的时候可能上一个拿的是 i - 8, 所以需要考虑 8 个位置.
unsigned m, n;
unsigned A, B, C, D, t;
unsigned Cnt(0), Ans(0), Tmp(0);
unsigned Like[1015], Anger[1015], f[1015][150][2][10];
unsigned Cant[10];
inline void Clr() {
memset(f, 0x3f, sizeof(f));
memset(Like, 0x3f, sizeof(Like));
n = RD(), Ans = 0x3f3f3f3f;
}
signed main() {
t = RD();
Anger[0] = 0x3f3f3f3f;
Cant[0] = -1;
for (unsigned i(1); i <= 8; ++i) Cant[i] = Cant[i - 1] << 1;
for (unsigned T(1); T <= t; ++T) {
Clr();
for (unsigned i(1); i <= n; ++i) Like[i] = RD(), Anger[i] = RD();
f[2][0][0][1] = 0, Anger[n + 1] = 0;
for (unsigned i(2), Now(0x3f3f3f3f); i <= 8; ++i) {
Now = min(Now, Anger[i - 1] + i - 1);
if (i > Now) break;
f[1][1 << (i - 2)][1][i - 1] = 0;
}
for (unsigned i(1); i <= n + 1; ++i) {
unsigned Mxj(1 << Anger[i]);
for (unsigned j(0); j < Mxj; ++j) {
unsigned Now(Cant[Anger[i]]);
for (unsigned No(1); No <= 8; ++No)
if (!((1 << (No - 1)) & j)) Now |= Cant[Anger[i + No]] << No;
if (j & Now) continue;
Now = i - 1;
for (unsigned k(0); k < 8; ++k) if (j & (1 << k)) Now = i + k + 1;
for (unsigned k(1); k <= 8; ++k) {
if (i < k) break;
if (Anger[i - k] < Now - i + k) continue;
unsigned Des(j << k);
Des |= (1 << (k - 1)) - 1;
for (unsigned l(1); l <= 8; ++l) {
if (i - k < l) break;
f[i][j][0][k] = min(f[i][j][0][k], f[i - k][Des][0][l] + (Like[i - k - l] ^ Like[i - k]));
}
for (unsigned l(1); l <= 8; ++l) {
// if(k == l) continue;
f[i][j][0][k] = min(f[i][j][0][k], f[i - k][Des][1][l] + (Like[i - k + l] ^ Like[i - k]));
}
}
for (unsigned k(1); k <= 8; ++k) {
if (!((1 << (k - 1)) & j)) continue;
if (Anger[i + k] < Now - i - k) continue;
unsigned Des(j ^ (1 << (k - 1)));
for (unsigned l(1); l <= 8; ++l) {
if (i < l) break;
f[i][j][1][k] = min(f[i][j][1][k], f[i][Des][0][l] + (Like[i - l] ^ Like[i + k]));
}
for (unsigned l(1); l <= 8; ++l) {
if (!((1 << (l - 1)) & Des)) continue;
f[i][j][1][k] = min(f[i][j][1][k], f[i][Des][1][l] + (Like[i + l] ^ Like[i + k]));
}
}
}
}
for (unsigned i(1); i <= 7; ++i) Ans = min(Ans, f[n + 1][0][0][i]);
printf("%u\n", Ans);
}
return Wild_Donkey;
}
AHOI2009
在棋盘上放置中国象棋中的炮, 使得没有炮能互相攻击, 求方案数.
问题转化为往棋盘上放点, 使得不存在三个点在一行或一列中.
状态 f_{i, j, k} 表示到第 i 行, 有 j 列有 1 个炮, k 列有 2 个炮.
\begin{aligned}
f_{i, j, k} = &f_{i - 1, j, k} +\\
&(n - k - j + 1)f_{i - 1, j - 1, k} +\\
&(j + 1)f_{i - 1, j + 1, k - 1} +\\
&\binom{n - k - j + 2}{2}f_{i - 1, j - 2, k} +\\
&\binom{j + 2}{2}f_{i - 1, j + 2, k - 2} +\\
&j(n - k - j + 1)f_{i - 1, j, k - 1}
\end{aligned}
代码使用滚动数组, 所以枚举顺序比较神奇, 轻松冲到最优解前几名.
const unsigned long long Mod(9999973);
unsigned long long Ans(0), f[105][105], C2[105];
unsigned m, n;
signed main() {
n = RD(), m = RD();
C2[0] = 0, f[0][0] = 1;
for (unsigned i(1); i <= n; ++i) C2[i] = (i * (i - 1)) >> 1;
for (unsigned i(1); i <= m; ++i) for (unsigned k(n); ~k; --k) for (unsigned j(n - k); ~j; --j) {
unsigned long long Tmp(0);
if(j) {
Tmp += f[j - 1][k] * (n - k - j + 1);
if(j > 1) Tmp += f[j - 2][k] * C2[n - k - j + 2];
}
if(k) {
Tmp += f[j][k - 1] * j * (n - k - j + 1) + f[j + 1][k - 1] * (j + 1);
if(k > 1) Tmp += f[j + 2][k - 2] * C2[j + 2];
}
f[j][k] = (f[j][k] + Tmp) % Mod;
}
for (unsigned i(0); i <= n; ++i) for (unsigned j(0); j + i <= n; ++j) Ans += f[i][j];
printf("%llu\n", Ans % Mod);
return Wild_Donkey;
}
P5005
在棋盘上放置中国象棋中的马, 使得没有马能互相攻击或单向攻击, 求方案数.
仍然状压两位, f_{i, j, k} 表示到第 i 行, 第 i 行状态为 k, 第 i - 1 行状态为 j 的状态.
f_{i, k, l} = \sum f_{i - 1, j, k}\\
!(((j << 2) \And (((1 << m) - 1) \oplus ((j \And k) << 1))) | ((j >> 2) \And (((1 << m) - 1) \oplus ((j \And k) >> 1))) \And k),\\
!(((j << 1) \And (((1 << m) - 1) \oplus (k \And (k << 1)))) | ((j >> 1) \And (((1 << m) - 1) \oplus (k \And (k >> 1)))) \And l),\\
!(((k << 2) \And (((1 << m) - 1) \oplus ((k \And l) << 1))) | ((k >> 2) \And (((1 << m) - 1) \oplus ((k \And l) >> 1))) \And l),\\
这个题太毒了, 必须滚数组, 因为它的内存只开了 1MB.
const unsigned long long Mod(1000000007);
unsigned long long Ans(0);
unsigned f[65][65], g[65][65];
unsigned m, n, M;
unsigned A, B, C, D, t;
unsigned Cnt(0), Tmp(0);
signed main() {
n = RD(), M = 1 << (m = RD());
g[0][0] = 1;
for (unsigned i(1); i <= n; ++i) {
for (unsigned j(0); j < M; ++j) {
for (unsigned k(0); k < M; ++k) {
unsigned Verjk(j & k);
if(!((((j << 2) & ((M - 1) ^ (Verjk << 1))) | ((j >> 2) & ((M - 1) ^ (Verjk >> 1)))) & k & (M - 1))) {
for (unsigned l(0); l < M; ++l) {
unsigned Ver(k & l), No(0), Hor(k & (k << 1));
No |= (((j >> 1) & ((M - 1) ^ (Hor >> 1))) | ((j << 1) & ((M - 1) ^ Hor)));
No |= (((k >> 2) & ((M - 1) ^ (Ver >> 1))) | ((k << 2) & ((M - 1) ^ (Ver << 1))));
if(!(No & l & (M - 1))) {
f[k][l] += g[j][k];
if(f[k][l] >= Mod) f[k][l] -= Mod;
}
}
}
}
}
memcpy(g, f, sizeof(f));
memset(f, 0, sizeof(f));
}
for (unsigned i(0); i < M; ++i) {
for (unsigned j(0); j < M; ++j) {
Ans += g[i][j];
}
}
printf("%llu\n", Ans % Mod);
return Wild_Donkey;
}
TJOI2015
每个点的范围是 3 * p, 仍然求放点使其不能攻击的方案数.
因为转移规则是一个矩阵, 所以不方便使用位运算判断, 用转移矩阵对状态进行转移.
预处理每个行状态能转移到下一行的哪个状态, 建一个 2^m * 2^m 的矩阵, 用矩阵快速幂加速转移, 复杂度 O(8^m \log n).
vector <char> To[65];
unsigned List[65], Do[65], f[65], g[65];
unsigned M, m, n, p, P, Q;
unsigned A, B, C, D, t;
unsigned Cnt(0), Ans(0), Tmp(0);
char Flg(0);
struct Matrix {
unsigned Val[65][65];
inline Matrix operator * (Matrix& x) {
Matrix TmpT;
for (unsigned i(1); i <= Cnt; ++i) {
memset(TmpT.Val[i], 0, (Cnt + 1) << 2);
for (unsigned j(1); j <= Cnt; ++j) {
for (unsigned k(1); k <= Cnt; ++k) {
TmpT.Val[i][j] += Val[i][k] * x.Val[k][j];
}
}
}
return TmpT;
}
}Mu, Eps;
signed main() {
n = RD(), M = 1 << (m = RD()), p = RD(), Q = p - (P = RD()) - 1;
for (unsigned j(0); j < p; ++j) B |= (RD() << j);
for (unsigned j(0); j < p; ++j) A |= (RD() << j);
for (unsigned j(p - 1); ~j; --j) C |= (RD() << j);
for (unsigned i(0); i < M; ++i, Flg = 0) {
for (unsigned j(0); (j < m) && (!Flg); ++j) if((1 << j) & i) {
i ^= (1 << j);
if(j < P) Flg = (i & (A >> (P - j))) ? 1 : 0;
else Flg = (i & (A << (j - P))) ? 1 : 0;
i ^= (1 << j);
}
if(!Flg) List[++Cnt] = i;
}
for (unsigned i(1); i <= Cnt; ++i) {
for (unsigned j(0); j < M; ++j) if((1 << j) & List[i]) {
if(j < P) Do[i] |= (B >> (P - j));
else Do[i] |= (B << (j - P));
if(j < Q) Do[i] |= (C >> (Q - j));
else Do[i] |= (C << (j - Q));
}
}
for (unsigned j(1); j <= Cnt; ++j) for (unsigned k(1); k <= Cnt; ++k)
Eps.Val[j][k] = !(Do[j] & List[k]);
for (unsigned i(1); i <= Cnt; ++i) Mu.Val[i][i] = 1;
while (n) {
if(n & 1) Mu = Mu * Eps;
n >>= 1, Eps = Eps * Eps;
}
for (unsigned i(1); i <= Cnt; ++i) Ans += Mu.Val[1][i];
printf("%u\n", Ans);
return Wild_Donkey;
}
NOIP2017
给一个无向图, 求一个生成树使得代价最小, 一个生成树的代价是边的代价之和, 每条边的代价是边的权值和边下端点深度的积. n \leq 12.
这个题 Prim 被 Hack 了, 详情见 RQY 的数据.
然后我当时感觉自己很牛逼, 发明的 O(2^nn^2) 做法.
设计状态 f_{i} 表示选择了 i 状态的点, O(2^n). 定义数组 g_{i, j} 表示状态 i 中, j 点的深度. 转移是枚举加入哪个点, 然后对于每个加入的点, 枚举它的父亲, 转移 O(n^2). 总复杂度 O(2^nn^2), 所以这个题 n 开到 15 也不是不能做.
emm, 这个做法必然是假了, 因为一个状态, 不一定是最优的, 什么意思, 就是说一个集合表示的状态, 它所记录的权值只是一个最优局部解, 有后效性, 所以是可以假的, 小的 Hack 数据不好构造, 所以就不构造了.
这个题真正的解法, 是一层一层地转移. 设计状态 f_{i, j} 表示已经构造了 i 层, 这 i 层包含了集合 j 的点. 转移时枚举 j 的子集 k, 从状态 f_{i - 1, k} 转移而来, 它关于 j 的补集中的点作为第 i 层, 因为不知道 k 中哪个点在第 i 层, 所以就默认都在第 i - 1 层, 这样的答案不会更大, 而这种方式会枚举所有的情况, 所以不会得到错误的答案.
f_{i, j} = \min_{k \subseteq i} (f_{k, j - 1} + i\sum_{a \in (k \oplus i)}\min_{b \in k}E_{a, b})
枚举所有集合的子集是 O(3^n), 每次枚举哪个点连哪个点是 O(n^2), 阶段是 O(n), 总复杂度 O(n^33^n).
可以预处理出每个点 j 到一个集合 i 的最短距离 Mn_{i, j}, 把转移优化到 O(n), 总复杂度 O(On^23^n)
f_{i, j} = \min_{k \subseteq i} (f_{k, j - 1} + i\sum_{a \in (k \oplus i)} Mn_{k, a}
#define Lbt(x) ((x)&((~(x))+1))
unsigned N, m, n, A, B, C, t, Ans(0);
unsigned f[5005][15], E[15][15], Min[5005][15], Log[5005];
int main() {
N = 1 << (n = RD()), m = RD();
memset(E, 0x3f, sizeof(E));
memset(f, 0x3f, sizeof(f));
memset(Min, 0x3f, sizeof(Min));
for (unsigned i(1); i <= m; ++i) {
A = RD() - 1, B = RD() - 1;
E[A][B] = E[B][A] = min(E[B][A], RD());
}
for (unsigned i(0); i < n; ++i) Log[1 << i] = i;
for (unsigned i(1); i <= N; ++i) Log[i] = max(Log[i - 1], Log[i]);
for (unsigned i(0); i < N; ++i) {
unsigned TL(i ^ (N - 1));
for (unsigned j(i); j; j -= Lbt(j)) {
unsigned Frm(Log[Lbt(j)]);
for (unsigned k(TL); k; k -= Lbt(k)) {
unsigned To(Log[Lbt(k)]);
Min[i][To] = min(Min[i][To], E[Frm][To]);
}
}
}
f[0][0] = 0;
for (unsigned i(0); i < n; ++i) f[1 << i][0] = 0;
for (unsigned i(1); i < n; ++i) {
for (unsigned j(0); j < N; ++j) {
for (unsigned k(j); ; k = (j & (k - 1))) {
unsigned TL(j ^ k), Sum(0);
for (unsigned l(TL); l; l -= Lbt(l)) {
unsigned To(Log[Lbt(l)]);
Sum += Min[k][To];
}
f[j][i] = min(f[j][i], f[k][i - 1] + i * Sum);
if (!k) break;
}
}
}
printf("%u\n", f[N - 1][n - 1]);
return Wild_Donkey;
}
P3943
一个长为 n 的 0/1 串, 有 k 个 0, 每次允许取反特定长度的区间, m 种区间长度. 求最少取反几次得到 n 个 1.
对于区间取反问题, 首先想到的就是差分, 把原数组做异或差分得到新数组. 数据保证有解则差分数组 1 的总数一定是偶数, 每次考虑消除一对 1.
因为区间长度有限, 所以不能预处理每个长度的取反最少步数, 考虑其它方式.
我们用类似最短路的思想, 如果每个可行操作长度记为 a_i, 那么这个问题就相当于给 n + 1 个点跑单源最短路, 坐标相差为 a_i 的点之间都有长度为 1 的边.
因为有 k 个 0, 所以差分数组中的 1 一定不超过 2k 个, 我们把这 2k 个 1 的存在性作为状态, f_i 表示还剩 i 集合中的 1, 最少要操作多少次, 有方程:
f_i = \min_{j \in i, k \in i, j \neq k} f_{i \oplus \{j, k\}} + Dist_{j, k}
因为单源最短路的起点最多 2k 个, 所以一共跑 2k 次 O(mn\log (mn)) 的最短路就可以处理 Dist 数组了.
所以总复杂度 O(2^{2k} + nm \log (nm)).
#define INFi 0x3f3f3f3f
#define Lbt(x) ((x)&((~(x))+1))
bitset<40005> a, Vis;
unsigned Log[70005], Pop[70005], f[70005];
unsigned Ava[105], Di[40005], List[25], Dist[25][40005];
unsigned m, n, t, A, B, C, D;
unsigned Cnt(0), Ans(0), Tmp(0);
inline void Dij(unsigned S, unsigned* Dis) {
memset(Dis, 0x3f, (n + 2) << 2), Dis[S] = 0;
priority_queue<pair<unsigned, unsigned> > Q;
Vis = 0;
Q.push(make_pair(INFi, S)), Dis[S] = 0;
while (!Q.empty()) {
unsigned Cur(Q.top().second);
Q.pop();
if (Vis[Cur])return;
Vis[Cur] = 1;
for (unsigned i(1); i <= m; ++i) {
if ((Cur > Ava[i]) && (Dis[Cur - Ava[i]] > Dis[Cur] + 1))
Dis[Cur - Ava[i]] = Dis[Cur] + 1, Q.push(make_pair(INFi - Dis[Cur - Ava[i]], Cur - Ava[i]));
if ((Cur + Ava[i] <= n) && (Dis[Cur + Ava[i]] > Dis[Cur] + 1))
Dis[Cur + Ava[i]] = Dis[Cur] + 1, Q.push(make_pair(INFi - Dis[Cur + Ava[i]], Cur + Ava[i]));
}
}
}
signed main() {
n = RD() + 1, t = RD(), m = RD();
memset(Di, 0x3f, sizeof(Di)), Di[0] = 0;
memset(f, 0x3f, sizeof(f));
for (unsigned i(1); i <= t; ++i) A = RD(), a[A] = (a[A] ^ 1), a[A + 1] = (a[A + 1] ^ 1);
for (unsigned i(1); i <= m; ++i) Ava[i] = RD();
for (unsigned i(1); i <= n; ++i) if (a[i]) List[++Cnt] = i, Dij(i, Dist[Cnt]);
n = (1 << Cnt), f[n - 1] = 0;
for (unsigned i(0); i <= n; ++i) Pop[i] = Pop[i >> 1] + (i & 1);
for (unsigned i(0); (1 << i) <= n; ++i) Log[1 << i] = i;
for (unsigned i(1); i <= n; ++i) Log[i] = max(Log[i - 1], Log[i]);
for (unsigned i(n - 1); i; --i) {
if (Pop[i] & 1) continue;
for (unsigned j(i); j; j -= Lbt(j)) {
unsigned Frm(Log[Lbt(j)]);
for (unsigned k(j - Lbt(j)); k; k -= Lbt(k)) {
unsigned To(Log[Lbt(k)]), Tur(i ^ (1 << Frm) ^ (1 << To));
f[Tur] = min(f[Tur], f[i] + Dist[Frm + 1][List[To + 1]]);
}
}
}
printf("%u\n", f[0]);
return Wild_Donkey;
}
例题
给一个有障碍物的棋盘, 放 n 对人, 每对人不能和自己对应的人相邻, 求方案数.
设计状态 f_{i, j, k, l} 表示讨论到 (i, j), 轮廓线状态为 k, 已经填完了 l 对点的方案数.
每次转移一填填一对, 一个点填在 (i, j), 另一个点填在 (i, j) 前面的某个空位里, 需要讨论有多少个可行的空位, 然后把方案数乘这个数量.
需要统计 Em_{i, j} 表示扫描到 (i, j) 的时候的空位个数, 用它减去已经填了的和不能填的就是一共能填的数量.
最后乘一个排列数即可, 因为每对人本质不同.
NOI2015
为什么没有人用容斥呢? 本做法复杂度 O(3^8n).
给正整数 [2, n], 选两个不交子集, 使得两个子集中任意两个数互质. 求方案数.
分析性质, 发现对于每个质数 p, 两个数集中只有一个数集存在整除 p 的元素. 所以状态就是两个集合分别包含的质因数集合即可, 必须要求两个集合 \And 后是 0.
设 n 以内有 m 个质数, 则复杂度是 O(2^{2m}n).
发现 500 以内的数, 大于 19 的质因数最多有一个.
小于等于 19 的质数只有 2, 3, 5, 7, 11, 13, 17, 19, 共 8 个. 如果我们把包含大于 19 质因数的数字先剔除不计, 仅分配剩下这些质因数, 那么每个人的集合有 2^8 种情况, 两个人的状态数是 4^8 种, 因为两个人的集合不交, 每个元素的状态只有三种, 在第一个集合中, 在第二个集合中, 不存在, 所以一共是 3^8 种有效状态.
假设我们现在确定了决策完未剔除的数字后, 两个人的质因数集合. 那么对于剔除的数字, 我们可以枚举 19 后面的质数, 将所有以这个质数为最大质因数的数同时考虑, 枚举三种情况, 分别是把这些数按 19 以内的质因数约束分配到第一个人的集合里, 分配到第二个人的集合里, 不分配. 因为是按照确定的集合分配的, 所以 19 以内质因数是确定的, 19 以后的质因数也不会在待处理的数中出现, 所以是正确的.
我们把状态压成三进制, 称为集合 S. 每个 S 唯一对应一个有序二进制集合二元组 (A, B). 其中 A \And B = 0 表示两个人 19 以内的因数情况. S 的第 i 位是 0, 则 A, B 的第 i 位都为 0, 如果 S 的第 i 位是 1 或 2, 则分别对应 A 的第 i 位为 1 和 B 的第 i 位为 1.
对于每个 S, 我们把 [2, n] 每个数按照除以 19 以内所有质因数的结果分类, 可以算出 f_S 表示选出的两个不交子集各自的质因数, 分别是由 S 确定的 A, B 的子集的方案数.
定义三进制集合的 PopCnt 为这个集合不为 0 的元素个数. 我们发现对于一个方案 x, 这个方案两个人的 19 以内的质因数集合分别是 A_x 和 B_x, 这两个集合可以表示为三进制集合 S_x. 那么它不仅会被 f_{S_x} 统计, 还会被 S_x 的真超集的 f 值所统计.
那么对于一个满足自己对应的 S_x 的 PopCnt 为 i 的方案, 被 PopCnt 为 j 的 S (j \geq i) 所统计的次数, 也就是 S_x 的 PopCnt 为 j 超集数量, 即为:
g_{j, i} = \binom{8 - i}{8 - j} * 2^{j - i}
式子很容易理解, 组合数就是枚举哪些在 S_x 中为 0 的位置在 S 中也为 0, 后面的 2^{j - i} 则是讨论在 S_x 中为 0 但是在 S 中不为 0 的位置, 到底取 1 还是取 2, 互相独立, 满足乘法原理条件.
由上面的式子我们发现如果简单给 f_S 求和, 一个方案会被统计多次. 所以考虑用容斥把答案凑出来.
因为方案 x 的统计次数只和 S_x 的 PopCnt 有关, 所以 PopCnt 相同的 S 的 f_i 应当是同时考虑的, 所以我们定义
Sum_i = \sum_{PopCnt(S) = i} f_S
也就是说我们希望能有一个数列 a, 使得
Ans = \sum_{i = 0}^8 a_iSum_i
结合前面 g 的表达式, 那么对 a 的要求就是: 可以使得对于所有 i, 有
\sum_{j = i}^8 a_ig_{j, i} = 1
$$
\sum_{j = i}^n \binom{n - i}{n - j} * 2^{j - i} * (-1)^{n - j} = 1
$$
也就是说
$$
\sum_{j = i}^8 (-1)^{j}g_{j, i} = 1\\
a_i = (-1)^i
$$
至于原因, 我百思不得其解, 但是只需要对每个 $S$ 求方案数, 然后根据 $S$ 的元素数乘上相应的 $a$ 对答案进行统计即可.
```cpp
const unsigned M(6561);
const unsigned Tri[10] = { 1,3,9,27,81,243,729,2187,6561 };
const unsigned Prime[10] = { 2,3,5,7,11,13,17,19 };
vector <unsigned> Bel[505];
unsigned long long Tmp(0), Mod(998244353), Ans(0);
unsigned PopCnt[7005], Need[7005][2];
unsigned Stack[505], STop(0), Have[505];
unsigned m, n;
unsigned A, B, D, t;
unsigned Cnt(0);
signed main() {
n = RD(), Mod = RD();
for (unsigned i(2); i <= n; ++i) {
unsigned Ti(i);
for (unsigned j(0); j < 8; ++j) {
if (!(Ti % Prime[j])) Have[i] |= (1 << j);
while (!(Ti % Prime[j])) Ti /= Prime[j];
}
if (Ti > 1) Stack[++STop] = Ti;
Bel[Ti].push_back(i);
}
for (unsigned i(0); i < M; ++i) {
for (unsigned j(0); j < 8; ++j) {
unsigned Jth((i / Tri[j]) % 3);
if (Jth) Need[i][(Jth & 1) ? 0 : 1] |= (1 << j);
}
}
sort(Stack + 1, Stack + STop + 1);
STop = unique(Stack + 1, Stack + STop + 1) - Stack - 1;
for (unsigned i(0); i < M; ++i) PopCnt[i] = PopCnt[i / 3] + (bool)(i % 3);
for (unsigned i(0); i < M; ++i) {
Tmp = 1;
for (auto j : Bel[1]) {
if ((Have[j] & Need[i][0]) == Have[j]) { Tmp <<= 1; if (Tmp >= Mod) Tmp -= Mod; }
if ((Have[j] & Need[i][1]) == Have[j]) { Tmp <<= 1; if (Tmp >= Mod) Tmp -= Mod; }
}
for (unsigned j(1); j <= STop; ++j) {
A = 1, B = 1;
for (auto k : Bel[Stack[j]]) {
if ((Have[k] & Need[i][0]) == Have[k]) { A <<= 1; if (A >= Mod) A -= Mod; }
if ((Have[k] & Need[i][1]) == Have[k]) { B <<= 1; if (B >= Mod) B -= Mod; }
}
Tmp = Tmp * (A + B - 1) % Mod;
}
Ans += (PopCnt[i] & 1) ? (Mod - Tmp) : Tmp;
if (Ans >= Mod) Ans -= Mod;
}
printf("%llu\n", Ans);
return Wild_Donkey;
}
```
### [THU2012](https://www.luogu.com.cn/problem/P5933)
有 $n$ 个本质不同的点, 用若干条颜色不同的边将他们连成连通图, 求方案数. 每两个点 $i$, $j$ 之间有 $c_{i, j}$ 条边备选. 不允许出现重边, 自环.
我们用 $f_{i, S}$ 表示集合 $S$ 的点被连成 $i$ 个连通块的方案数. 用 $a_S$ 表示点集 $S$ 的连边方案数的总和, 也就是
$$
a_S = \prod_{i \in S, j \in S, i < j} c_{i, j}
$$
写出 $f$ 的转移方程
$$
f_{1, S} = a_S - \sum_{i = 2}^{|S|} f_{i, S}\\
f_{i, S} = \frac{\displaystyle{\sum_{S' \subset S}f_{i - 1, S'}f_{1, S - S'}}}{i}
$$
这个状态很好理解, 只要枚举 $S$ 的子集 $S'$ 从中分割出 $i - 1$ 个连通块, 然后让它的补集作为最后一个即可, 但是由于一个方案中, $S - S'$ 作为 $i$ 个连通块里任意一个都可以统计一次答案, 所以说每种情况会重复统计 $i$ 次, 最后需要除以 $i$.
$f_{1, 2^n - 1}$ 即为所求, 状态 $O(n2^n)$, 转移枚举子集, 复杂度 $O(n3^n)$, 对于 $n = 15$ 的数据跑了 $800ms$, 得了 $90'$.
```cpp
unsigned long long Mod(1000000007);
unsigned long long f[20][66000], Inv[20];
unsigned N, a[20][20], m, n, PopCnt[66000];
unsigned A, B, C, D, t;
unsigned Cnt(0), Ans(0), Tmp(0);
signed main() {
N = 1 << (n = RD()), Inv[0] = Inv[1] = 1;
for (unsigned i(0); i < n; ++i) for (unsigned j(0); j < n; ++j) a[i][j] = RD() + 1;
for (unsigned i(0); i < N; ++i) {
f[0][i] = 1;
for (unsigned j(0); j < n; ++j) if (i & (1 << j))
for (unsigned k(0); k < j; ++k) if (i & (1 << k))
f[0][i] = f[0][i] * a[j][k] % Mod;
}
for (unsigned i(0); i < N; ++i) PopCnt[i] = PopCnt[i >> 1] + (i & 1);
for (unsigned i(2); i <= n; ++i) {
Inv[i] = Mod - (Inv[Mod % i] * (Mod / i) % Mod); if (Inv[i] >= Mod) Inv[i] -= Mod;
}
f[0][1] = f[1][0] = 1;
for (unsigned i(1); i < N; ++i) {
f[1][i] = f[0][i];
for (unsigned k(PopCnt[i]); k > 1; --k) {
for (unsigned j((i - 1)& i); j; j = i & (j - 1)) if (PopCnt[j] >= k - 1)
f[k][i] = (f[k][i] + f[k - 1][j] * f[1][i ^ j]) % Mod;
f[k][i] = f[k][i] * Inv[k] % Mod;
f[1][i] += Mod - f[k][i];
if (f[1][i] >= Mod) f[1][i] -= Mod;
}
}
printf("%llu\n", f[1][N - 1]);
return Wild_Donkey;
}
```
根据数据范围 $n \leq 16$, 优化掉一个 $n$ 就能过了.
我一开始记录连通块数量 $i$ 作为连通块数量, 就是为了方便直接除以 $i$ 处理重复统计. 那么只要想办法让每个方案都被统计一次, 像背包问题一样给转移找一个顺序就可以少设以为状态了. 设 $f_S$ 为集合 $S$ 被连成一个连通块的方案数, 那么 $a_S - f_S$ 就是 $S$ 被连成不止一个连通块的方案数.
我们希望求出 $S$ 被连成不止一个连通块的方案数, 用来计算 $f_S$. 我们定义 $S$ 中编号最小的点为起点, 那么起点一定被一个连通块所包含, 这个连通块的点集记为 $S'$, 对于任何一个方案, $S'$ 是唯一的, 因为编号最小的点是唯一的. 所以我们只需要枚举所有编号最小的点存在的子集 $S'$, 直接统计就能防止重复. 这就要求 $S$ 的最高位在 $S'$ 中一定也是 $1$, 这个位代表起点. 我们可以通过判断 $S'$ 的二进制数值是否大于 $S - S'$ 快速判断 $S'$ 是否合法.
最后写出方程:
$$
f_S = a_S - \sum_{S' \subset S, S' > S - S'} f_{S'}a_{S - S'}
$$
状态数 $O(2^n)$, 枚举子集转移, 复杂度 $O(3^n)$, $n = 16$ 的数据跑了 $300ms$.
```cpp
unsigned long long Mod(1000000007);
unsigned long long f[66000], g[66000];
unsigned long long Tmp(0);
unsigned N, a[20][20], n;
signed main() {
N = 1 << (n = RD()), f[0] = 1;
for (unsigned i(0); i < n; ++i) for (unsigned j(0); j < n; ++j) a[i][j] = RD() + 1;
for (unsigned i(0); i < N; ++i) {
g[i] = 1;
for (unsigned j(0); j < n; ++j) if (i & (1 << j))
for (unsigned k(0); k < j; ++k) if (i & (1 << k))
g[i] = g[i] * a[j][k] % Mod;
}
for (unsigned i(1); i < N; ++i, Tmp = 0) {
for (unsigned j((i - 1)& i); j; j = i & (j - 1)) if (j > (i ^ j))
Tmp = (Tmp + f[j] * g[i ^ j]) % Mod;
f[i] = Mod + g[i] - Tmp;
if (f[i] >= Mod) f[i] -= Mod;
}
printf("%llu\n", f[N - 1]);
return Wild_Donkey;
}
```
### [AT2390](https://www.luogu.com.cn/problem/AT2390)
博弈论 + DP?
貌似博弈论和 DAG 往往同时出现...
先不管 DP, 考虑枚举所有边的存在状态, 如何判断一个状态是否先手必胜.
我们认为一个状态由两个棋子的坐标组成, 于是设布尔变量 $f_{i, j}$ 为第一个棋子在 $i$, 第二个棋子在 $j$ 是否为必胜态. 根据博弈论的基本原理 (能转移到必败态的状态必胜), 可以得到转移方程:
$$
f_{i, j} = [(\exist_{i \rightarrow k} (f_{k, j} = 0)) \lor (\exist_{j \rightarrow k} (f_{i, k} = 0))]
$$
所以就可以写出复杂度 $O(m ^ 2)$ 的判断可行性的代码:
```cpp
inline void Check() {
for (unsigned i(n); i; --i) {
for (unsigned j(n); j; --j) {
Con[i][j] = 0;
for (auto iT : N[i].E) if (iT.second)
Con[i][j] |= (1 ^ Con[iT.first - N][j]);
for (auto jT : N[j].E) if (jT.second)
Con[i][j] |= (1 ^ Con[i][jT.first - N]);
}
}
Ans += Con[1][2];
}
```
忽然发现我不懂什么是 SG 函数, 怒学. 设 $SG_i$ 为 $i$ 点的属性, 则当只有一个棋子时, 这个局面先手必胜的充要条件是对于这个棋子的所在点 $i$, 有 $SG_i > 0$.
我们把 $SG_i > 0$ 的点称为必胜点, 则 SG 值表示着一个必胜点的等级. 对于必败点, 其 SG 值为 $0$, 反之则必胜. $SG_i$ 等于 $i$ 能到达的所有点的 SG 值集合中最小的不被包含的数字.
对于两个棋子所在点的 SG 值为 $0$ 的时候, 它们不能走到 SG 为 $0$ 的任何点. 如果这个时候两个棋子都无路可走, 先手立刻失败. 如果这时有棋子可以走, 则走到的点 SG 为 $x$, 且 $x > 0$, 后手可以立刻把这个棋子移动到另一个 SG 为 $0$ 的点上. 因为是 DAG, 所以每个状态至多经过一次, 所以迟早会走到先手无路可走的状态. 所以 SG 都为 $0$ 的状态先手必败.
由 SG 值的定义我们知道, 一个必胜点 $i$ 一定能走到 SG 值为 $(SG_i, 0]$ 的点. 如果两个棋子的 SG 值相等, 那么先手把棋子移动到 SG 为 $x$ 的点, 后手一定也有方式可以将另一个棋子移动到 SG 值为 $x$ 的点, 先手首先将一个棋子所在点的 SG 值变成 $0$, 后手紧接着把另一个棋子所在点的 SG 值变为 $0$, 这时先手必败. 因此两个棋子所在位置 SG 值相同先手必败.
如果两个棋子 SG 值不同, 设一个是 $x$, 一个是 $y$, $x > y$. 先手可以直接把所在位置 SG 为 $x$ 的棋子移动到 SG 值为 $y$ 的位置上, 直接得到两个棋子位置同为 $y$ 的必败态, 后手必败.
因此对于一个方案, 可以求每个位置的 SG 值, 然后判断 $1$ 号点和 $2$ 号点的 SG 值是否相等即可. 得到了 $O(n^22^m)$ 的判断函数.
```cpp
inline void Check() {
for (unsigned i(n); i; --i) {
memset(Tmp, 1, sizeof(Tmp));
for (auto j : N[i].E) if (j.second) Tmp[Sig[j.first - N]] = 0;
for (unsigned j(0); j <= n; ++j) if (Tmp[j]) { Sig[i] = j; break; }
}
Ans += (Sig[1] ^ Sig[2]) ? 1 : 0;
}
```
接下来是避免枚举连边情况, 考虑状压. 设计状态 $f_{i, S}$ 表示集合 $S$ 中 SG 值都 $\leq i$, 并且集合 $2^n - 1 - S$ 中所有点的 SG 值都至少是 $i + 1$ 的方案数. $f_{i, S}$ 的每个方案中, $S$ 集合中的点到所有点和所有点到 $S$ 集合中的点的边的存在情况已经确定, $2^n - 1 - S$ 中的点之间的边的存在情况尚未确定.
转移是枚举子集, 将 $S$ 的一个非空子集 $S'$ 作为所有 SG 值为 $i + 1$ 的点的集合, 只需要计算 $S'$ 中的点随意向 $2^n - 1 - S$ 中的点连边的方案数乘 $2^n - 1 - S$ 中的每个点至少连一条向 $S'$ 的方案数即可转移.
我们用 $b_{i, A}$ 表示点 $i$ 到 $A$ 集合的边数, 就可以写出方程:
$$
f_{i, S} += f_{i - 1, S - S'} (\prod_{j \in S'} 2^{b_{j, 2^n - 1 - S}}) (\prod_{j \in 2^n - 1 - S} 2^{b_{j, S'} - 1})
$$
这个式子很好理解, 只要从 $f_{i - 1, S - S'}$ 的情况中, 把 $S'$ 中的点作为 SG 为 $i + 1$ 的点, 它们不能内部连边, 这样就没有通往 SG 为 $i + 1$ 的边, 但是可以向 SG 大于 $i + 1$ 的点连边, 所以随意连接 $2^n - 1 - S$ 中的点, 对于 $2^n - 1 - S$ 的点, 它们已经可以通往 $[0, i]$ 所有 SG 值了, 现在要求它们能够连向 SG 为 $i + 1$ 的点, 随意连的方案里面只有一种是一条都没连的, 所以只要减 $1$ 然后连乘起来就好了.
我们这样算出来的方案对答案没有用处, 但是通过约束 $S'$ 必须不只包含 $1, 2$ 其中之一 (也就是要么两个都包含, 否则都别包含), 就可以使得每种情况里, $1, 2$ 两点的 SG 值相等. 因为所有的方案最大 SG 值为 $n - 1$ (理论上强制 $1, 2$ SG 相等, 最大 SG 值只有 $n - 2$), 所以答案就可以表示为:
$$
2^m - \sum_{i = 0}^{n - 1} f_{i, 2^n - 1}
$$
也就是所有的情况减去 $1, 2$ SG 值相等的所有情况数. 状态 $O(n2^n)$, 枚举子集并且枚举集合元素转移, 复杂度 $O(n^23^n)$.
```cpp
const unsigned long long Mod(1000000007);
unsigned long long Ans(0), f[16][33005], Bin[200];
vector <unsigned> Have[33005];
unsigned a[20][33005], m, n, N;
unsigned A, B, C, D, t;
char Li[20][20];
signed main() {
N = (1 << (n = RD())) - 1, m = RD(), Bin[0] = 1;
for (unsigned i(1); i <= m; ++i) { Bin[i] = Bin[i - 1] << 1; if (Bin[i] >= Mod) Bin[i] -= Mod; }
for (unsigned i(1); i <= m; ++i) A = RD() - 1, Li[A][RD() - 1] = 1;//A to Li[A]
for (unsigned i(0); i <= N; ++i)//Set Contain
for (unsigned j(0); j < n; ++j)
if (i & (1 << j)) Have[i].push_back(j);
for (unsigned i(0); i < n; ++i) {//Point to Set
for (unsigned j(i + 1); j < n; ++j) if (Li[i][j]) a[i][1 << j] = 1;
for (unsigned j(0); j <= N; ++j) a[i][j] = a[i][j - Lbt(j)] + a[i][Lbt(j)];
}
for (unsigned i(0); i <= N; ++i) {//Side Case
f[0][i] = 1;
for (auto j : Have[i]) f[0][i] = f[0][i] * Bin[a[j][N ^ i]] % Mod;
for (auto j : Have[N ^ i]) f[0][i] = f[0][i] * (Bin[a[j][i]] - 1) % Mod;
}
for (unsigned i(1); i < n; ++i) {
for (unsigned j(0); j <= N; ++j) {
for (unsigned k(j); k; k = ((k - 1) & j)) {
if ((!(k & 3)) || ((k & 3) == 3)) {
unsigned long long Tmp(1);
for (auto Poi : Have[N ^ j]) Tmp = Tmp * (Bin[a[Poi][k]] - 1) % Mod;
for (auto Poi : Have[k]) Tmp = Tmp * Bin[a[Poi][N ^ j]] % Mod;
f[i][j] = (f[i][j] + f[i - 1][j ^ k] * Tmp) % Mod;
}
}
}
}
Ans = Bin[m];
for (unsigned i(0); i < n; ++i) {
Ans = Mod + Ans - f[i][N];
if (Ans >= Mod) Ans -= Mod;
}
printf("%llu\n", Ans);
return Wild_Donkey;
}
```
### [P4363](https://www.luogu.com.cn/problem/P4363)
一个棋盘, 每个格子有两个值 $a_{i, j}$ 和 $b_{i, j}$, 先手选 $(i, j)$ 获得收益 $a_{i, j}$, 后手选 $(i, j)$ 获得 $b_{i, j}$. 每个格子 $(i, j)$ 选当且仅当除了它以外, $x \in [1, i]$, $y \in [1, j]$ 的所有 $(x, y)$ 都已经选了. 若每个人采用最优策略, 求最后双方的差值.
因为每个格子选择的条件, 每个状态可以表示为一个从左下角到右上角, 只能向右和向上走的长度为 $n + m$ 的折线, 折线左上方都选了, 左下都没选. 折线可以用长度 $n + m$ 的二进制数来表示, `0` 表示向上, `1` 表示向右, 因为有 $n$ 个 `0`, 所以状态数为 $\binom {n + m}n$ 种.
将 $[1, \binom {n + m}n]$ 的数作为状态值和对应的二进制数映射, 然后对它进行转移. 我本来是想设 $f_{S}$ 为状态 $S$ 的答案, 也就是都按最优策略选的结果.
一开始尝试把所有能转移来的状态里找一个最优的作为 $f_{S}$ 的值, 但是样例过不了, 因为这样转移的前提是最优的前一个状态必须存在, 但是实际上一个人选择一个格子的时候是不能选择从什么状态的基础上选的, 所以会错误.
后来把所有可以转移来的状态里找一个最劣的作为 $f_{S}$ 的值, 可以过样例, 但是只有 $30'$, 原因也很简单, 如果每次都按最劣的转移, 确实可以保证决策后答案一定不会更劣, 但是这样最优策略却无从体现. 比如一个状态 $S$, 可以从 $S_1$, $S_2$ 转移而来, 而 $S_1$, $S_2$ 都可以从 $S_3$. 我需要决策选择 $S_1$ 还是 $S_2$ 转移到 $S$, 这时 $S_2$ 更劣, 但是我可以在 $S_3$ 的决策中直接选择转移到 $S_1$, 避开 $S_2$ 的状态. 这样就证明了这种转移的错误性.
百思不得其解的我去看题解, 发现题解的状态设计和我唯一的不同的是, 我看到是过去, 他们看的是未来. $f_S$ 表示从 $S$ 状态开始, 都按最优策略选择可以让差值变化多少. 一开始我认为, 这个问题是对称的, 正如从左上角开始选择和从右下角开始舍弃是一样的, 但是这只是过程上的对称性, 但不是策略上的对称, 左上的格子和右下的格子是因果关系. 打个比方, 光学中说光路可逆, 但是光的传播是有方向的.
我选择一个格子, 它会影响之后我和对手的选择可能性或者说自由度, 所以在这一点上, 最优策略应当不是对称的. 为了证明我的结论, 我把样例旋转 $180^{\circ}$ 并且互换 $a$, $b$ 后, 喂给标程, 果然跑出了和我一开始的程序相同的结果 $\sum a - \sum b = 6$ (旋转互换后, 标称跑出来的是 $\sum b - \sum a = -6$, 本质相同).
因此便说明了这个题只有倒着跑才能过的合理性: 倒着转移不存在前驱状态不可能到达的情况, 因为前驱状态是否能到达是我这一步的决策决定的, 掌握在我自己手中, 而不是历史手中.
但是我懒得改代码了, 就利用了一波问题的对称性, 直接把输入的两个矩阵都旋转 $180^{\circ}$, 然后考虑最后一个格子是谁选的, 也就是格子数量奇偶性, 如果是偶数, 就交换 $a$, $b$. 然后直接跑一边一开始写的 DP, 最后输出答案时别忘了如果交换了 $a$, $b$, 得到的答案是 $\sum b - \sum a$, 需要取反.
状态数 $\binom{n + m}n$, 转移 $O(n + m)$, 复杂度是 $(n + m)\binom{n + m}n$.
```cpp
unordered_map <unsigned, unsigned> Find;
int a[15][15], b[15][15], f[200005];
unsigned List[200005], Step[200005];
unsigned m, n, nm, Bnm;
unsigned A, B, C, D, t;
unsigned Cnt(0), Ans(0), Tmp(0);
inline unsigned PpC(unsigned x) {
unsigned PRt(0);
for (;x;x -= Lbt(x)) ++PRt;
return PRt;
}
inline void DFS(unsigned Now, unsigned Dep, unsigned Used) {
if (Dep == nm) {
if (Used == m) List[++Cnt] = Now, Find[Now] = Cnt;
return;
}
if (Used > m) return;
DFS(Now, Dep + 1, Used);
DFS(Now | (1 << Dep), Dep + 1, Used + 1);
}
signed main() {
n = RD(), m = RD(), Bnm = (1 << ((nm = n + m) - 1)) - 1;
if ((n * m) & 1) {
for (unsigned i(n); i; --i) for (unsigned j(m); j; --j) a[i][j] = RD();
for (unsigned i(n); i; --i) for (unsigned j(m); j; --j) b[i][j] = RD();
}
else {
for (unsigned i(n); i; --i) for (unsigned j(m); j; --j) b[i][j] = RD();
for (unsigned i(n); i; --i) for (unsigned j(m); j; --j) a[i][j] = RD();
}
DFS(0, 0, 0);
for (unsigned i(1); i <= Cnt; ++i) for (unsigned j(0), Thi(n); j < nm; ++j)
if (List[i] & (1 << j)) Step[i] += Thi; else --Thi;
for (unsigned i(2); i <= Cnt; ++i) {
unsigned Now(List[i]), Need(((~Now) >> 1) & Now & Bnm);
if (Step[i] & 1) {
f[i] = 0xafafafaf;
for (unsigned j(Need); j; j -= Lbt(j)) {
unsigned Dest(Find[Now ^ (3 * Lbt(j))]);
f[i] = max(f[i], f[Dest] + a[n - PpC((Lbt(j) - 1) & (~Now))][1 + PpC((Lbt(j) - 1) & Now)]);
}
}
else {
f[i] = 0x3f3f3f3f;
for (unsigned j(Need); j; j -= Lbt(j)) {
unsigned Dest(Find[Now ^ (3 * Lbt(j))]);
f[i] = min(f[i], f[Dest] - b[n - PpC((Lbt(j) - 1) & (~Now))][1 + PpC((Lbt(j) - 1) & Now)]);
}
}
}
printf("%d\n", ((n * m) & 1) ? f[Cnt] : (-f[Cnt]));
return Wild_Donkey;
}
```
## Day22: 模拟赛
### A
给一个数 $S$, 和一个序列 $a$, 每次可以选择一个数, 使得 $S$ 变成 $S + a_i$ 或 $Sa_i$, 每个数用一次, 求操作后 $S$ 最大值.
升序排序, 贪心, 一定有一个界, 使得在此之前都选 $S + a_i$, 之后都选 $Sa_i$. 而这个界限可以贪心地判断考虑到每个数字时 $S + a_i$ 和 $Sa_i$ 的大小.
由于 $S$ 和给出序列的长度两个范围看反了, 所以数组开小了, 而且没开 `long double`, 所以直接爆炸.
```cpp
unsigned m, n, Cnt(0), A, B, C, D, t;
long double Ans, a[100005];
inline void Clr() {}
int main() {
scanf("%LF", &Ans), n = RD();
for (register unsigned i(1); i <= n; ++i) {
scanf("%LF", &a[i]);
}
sort(a + 1, a + n + 1);
for (register unsigned i(1); i <= n; ++i) {
if(a[i] <= 1) {
Ans += a[i];
continue;
}
if(a[i] * Ans > a[i] + Ans) {
Ans *= a[i];
} else {
Ans += a[i];
}
}
printf("%.9LF\n", Ans);
return Wild_Donkey;
}
```
### B
题假了, 爆零人站起来了.
### C
先考虑只有两个值的情况, 容易想到贪心, 按 $a_i - b_i$ 升序排序, 前 $B$ 个都选 $b$, 后 $A$ 个都选 $a$.
首先想到了 DP, 状态 $f_{i, j, k}$ 表示前 $i$ 个物品, 已经选了 $j$ 个 $a$, $k$ 个 $b$, $i - j - k$ 个 $c$ 的最大收益.
$$
f_{i, j, k} = max(f_{i - 1, j - 1, k} + a_{i}, f_{i - 1, j, k - 1} + b_{i}, f_{i - 1, j, k} + c_{i})
$$
状态 $O(n^3)$, 转移 $O(1)$, 时间复杂度 $O(n^3)$, 滚动数组后空间复杂度 $O(n^2)$. 可以得到 $60'$.
```cpp
unsigned long long a[3][300005], f[5005][5005];
unsigned m, n, Cnt(0), A, B, C, D, t, Ans(0), Tmp(0);
inline void Clr() {}
int main() {
n = RD(), A = RD(), B = RD();// C = RD();
for (register unsigned i(1); i <= n; ++i) {
a[0][i] = RD(), a[1][i] = RD(), a[2][i] = RD();
}
for (register unsigned i(1); i <= n; ++i) {
for (register unsigned j(i - 1); j; --j) {
f[j][i - j] = max(f[j - 1][i - j] + a[0][i], f[j][i - j - 1] + a[1][i]);
}
f[i][0] = f[i - 1][0] + a[0][i];
f[0][i] = f[0][i - 1] + a[1][i];
for (register unsigned j(i - 1); j; --j) {
for (register unsigned k(i - j - 1); k; --k) {
f[j][k] = max(max(f[j - 1][k] + a[0][i], f[j][k - 1] + a[1][i]), f[j][k] + a[2][i]);
}
}
for (register unsigned j(i - 1); j; --j) {
f[j][0] = max(f[j - 1][0] + a[0][i], f[j][0] + a[2][i]);
f[0][j] = max(f[0][j - 1] + a[1][i], f[0][j] + a[2][i]);
}
f[0][0] = f[0][0] + a[2][i];
}
printf("%llu\n", f[A][B]);
return Wild_Donkey;
}
```
能得 $60'$ 的算法还有费用流, 开三个点分别连向汇点免费的, 容量为 $A$, $B$, $C$ 的边. 然后从源点向每个物品连免费的容量为 $1$ 的边, 然后每个物品分别向 $A$, $B$, $C$ 点连接容量为 $1$, 费用分别是 $a_i$, $b_i$, $c_i$ 的边, 跑最大费用最大流即可.
接下来是正解:
如果有三个值, 仍先按 $a_i - b_i$ 升序排序, 假设已经把选 $c$ 的 $C$ 个物品删掉了, 这时剩下的 $A + B$ 个物品仍应该是前 $B$ 个选 $b$, 后 $A$ 个选 $a$. 因此在排好序的 $n$ 个物品的序列中, 一定存在一个分界线, 它左边除了 $b$ 就是 $c$, 它右边除了 $a$ 就是 $c$.
假设我们已经知道, 分界线是 $x$, 也就是说 $[1, x]$ 中, 有 $B$ 个选 $b$, $x - B$ 个选 $C$.
我们已经知道了只有两种选择的时候如何贪心, 直接选择 $x$ 个数中的前 $B$ 大的 $b_i - c_i$ 的物品选 $b$ 即可.
但是如果对于每个分界点都这样判断, 无疑是非常慢的, 定义两个数组, $f_i$ 和 $g_i$, 分别代表 $[1, i]$ 中前 $B$ 大的 $b_i - c_i$ 值之和, 和 $[i, n]$ 中前 $A$ 大的 $a_i - c_i$ 值之和. 到时候只要取 $f_{i} + g_{i + 1} + SumC$ 的最大值即可.
如何求 $f$ 和 $g$, $f$ 的下标范围是 $[B, n]$, 而 $f_{B}$ 显然是 $\displaystyle{\sum_{i = 1}^{i \leq B} b_i - c_i}$, 接下来的每个 $f_i$, 都是在上一个版本的基础上加入当前位置的 $b_i - c_i$. 然后删去最小值得到的总和, 每次弹出最小值可以用堆维护, $g$ 同理. 这样就可以 $O(n \log n)$ 求出 $f$ 和 $g$. 最后 $O(n)$ 扫描统计答案即可.
```cpp
struct Gift {
unsigned V1, V2;
inline const char operator<(const Gift &x) const{
return (this->V1 + x.V2) > (x.V1 + this->V2);
}
}G[300005];
unsigned V3[300005], m, n, Cnt(0), A, B, C, D, t;
unsigned long long Ans(0), f[300005], g[300005], Tmp;
priority_queue<unsigned, vector<unsigned>, greater<unsigned> > Q;
int main() {
n = RD(), A = RD(), B = RD(); C = n - B;
for (register unsigned i(1), Min; i <= n; ++i) {
G[i].V1 = 1000000000 + RD(), G[i].V2 = 1000000000 + RD(), Ans += (V3[i] = RD());
G[i].V1 -= V3[i], G[i].V2 -= V3[i];
}
sort(G + 1, G + n + 1), Ans -= (unsigned long long)1000000000 * (A + B);
for (register unsigned i(1); i <= A; ++i) {
Tmp = G[i].V1;
Q.push(Tmp);
f[i] = f[i - 1] + Tmp;
}
for (register unsigned i(A + 1); i <= n; ++i) {
Tmp = G[i].V1;
Q.push(Tmp);
f[i] = f[i - 1] + Tmp - Q.top();
Q.pop();
}
while (Q.size()) Q.pop();
for (register unsigned i(n); i > C; --i) {
Tmp = G[i].V2;
Q.push(Tmp);
g[i] = g[i + 1] + Tmp;
}
for (register unsigned i(C); i; --i) {
Tmp = G[i].V2;
Q.push(Tmp);
g[i] = g[i + 1] + Tmp - Q.top();
Q.pop();
}
Tmp = 0;
for (register unsigned i(A); i <= C; ++i) {
Tmp = max(Tmp, f[i] + g[i + 1]);
}
printf("%llu\n", Ans + Tmp);
return Wild_Donkey;
}
```
### D
据说正解是矩阵乘法或可持久化平衡树, 但是我们不管这么多, 直接踩一下标算.
开 $20$ 棵动态开点线段树, 通过交换和共用儿子来操作, 通过节点分裂保证每一行互不干扰, 复杂度 $O(m \log n)$.
```cpp
unsigned m, n, q, Cnt(0), A, P, B, C, D, t, Ans(0), Tmp(0);
const unsigned MOD(998244353);
inline void Clr() {}
struct Node {
Node *LS, *RS;
unsigned Val, Tag, Deg;
}*Root[25], N[50000005], *CntN(N);
inline void New(Node *x, Node *y) {
x->Deg = 1;
x->Val = y->Val;
x->Tag = y->Tag;
x->LS = y->LS;
x->RS = y->RS;
if(x->LS) ++(x->LS->Deg);
if(x->RS) ++(x->RS->Deg);
--(y->Deg);
}
inline void PsDw(Node *x, const unsigned Len) {
if(!(x->LS)) x->LS = ++CntN, x->LS->Deg = 1;
if(!(x->RS)) x->RS = ++CntN, x->RS->Deg = 1;
if(x->LS->Deg > 1) {
New(++CntN, x->LS);
x->LS = CntN;
}
if(x->RS->Deg > 1) {
New(++CntN, x->RS);
x->RS = CntN;
}
if(x->Tag) {
x->LS->Tag += x->Tag;
if(x->LS->Tag >= MOD) x->LS->Tag -= MOD;
x->LS->Val = ((unsigned long long)(x->Tag) * ((Len + 1) >> 1) + x->LS->Val) % MOD;
x->RS->Tag += x->Tag;
if(x->RS->Tag >= MOD) x->RS->Tag -= MOD;
x->RS->Val = ((unsigned long long)(x->Tag) * (Len >> 1) + x->RS->Val) % MOD;
x->Tag = 0;
}
return;
}
void Qry(Node *x, unsigned L, unsigned R) {
if((B <= L) && (R <= C)) {
Ans += x->Val;
if(Ans >= MOD) Ans -= MOD;
return;
}
register unsigned Mid((L + R) >> 1);
PsDw(x, R - L + 1);
if(B <= Mid) {
Qry(x->LS, L, Mid);
}
if(C > Mid) {
Qry(x->RS, Mid + 1, R);
}
return;
}
void Chg(Node *x, unsigned L, unsigned R) {
if((B <= L) && (R <= C)) {
x->Tag += D;
if(x->Tag >= MOD) x->Tag -= MOD;
x->Val = (((unsigned long long)D * (R - L + 1)) + x->Val) % MOD;
return;
}
register unsigned Mid((L + R) >> 1);
PsDw(x, R - L + 1);
if(B <= Mid) {
Chg(x->LS, L, Mid);
}
if(C > Mid) {
Chg(x->RS, Mid + 1, R);
}
x->Val = x->LS->Val + x->RS->Val;
if(x->Val >= MOD) x->Val -= MOD;
return;
}
void Swap(Node *x, Node *y, unsigned L, unsigned R) {
if(L == R) return;
register unsigned Mid((L + R) >> 1);
PsDw(x, R - L + 1);
PsDw(y, R - L + 1);
if(C <= Mid) {
if((C <= L) && (Mid <= D)) {
swap(x->LS, y->LS);
} else {
Swap(x->LS, y->LS, L, Mid);
}
}
if(D > Mid) {
if((C <= Mid + 1) && (R <= D)) {
swap(x->RS, y->RS);
} else {
Swap(x->RS, y->RS, Mid + 1, R);
}
}
x->Val = x->LS->Val + x->RS->Val;
if(x->Val >= MOD) x->Val -= MOD;
y->Val = y->LS->Val + y->RS->Val;
if(y->Val >= MOD) y->Val -= MOD;
return;
}
void Copy(Node *x, Node *y, unsigned L, unsigned R) {
if(L == R) return;
register unsigned Mid((L + R) >> 1);
PsDw(x, R - L + 1);
PsDw(y, R - L + 1);
if(C <= Mid) {
if((C <= L) && (Mid <= D)) {
y->LS = x->LS;
++(y->LS->Deg);
} else {
Copy(x->LS, y->LS, L, Mid);
}
}
if(D > Mid) {
if((C <= Mid + 1) && (R <= D)) {
y->RS = x->RS;
++(y->RS->Deg);
} else {
Copy(x->RS, y->RS, Mid + 1, R);
}
}
x->Val = x->LS->Val + x->RS->Val;
if(x->Val >= MOD) x->Val -= MOD;
y->Val = y->LS->Val + y->RS->Val;
if(y->Val >= MOD) y->Val -= MOD;
return;
}
int main() {
n = RD(), m = RD(), q = RD();
for (register unsigned i(1); i <= n; ++i) {
Root[i] = ++CntN;
}
for (register unsigned i(1); i <= q; ++i) {
A = RD(), P = RD(), B = RD(), C = RD();
switch (A) {
case (0) :{
Ans = 0, Qry(Root[P], 1, m);
printf("%u\n", Ans);
break;
}
case (1) :{
D = RD(), Chg(Root[P], 1, m);
break;
}
case (2) :{
D = RD();
if(B == P) break;
Swap(Root[P], Root[B], 1, m);
break;
}
case (3) :{
D = RD();
if(B == P) break;
Copy(Root[P], Root[B], 1, m);
break;
}
}
}
return Wild_Donkey;
}
```
## Day23: 数位 DP
### [SCOI2009](https://www.luogu.com.cn/problem/P2657)
求区间 $[L, R]$ 的数中, 有多少是相邻数位的数字相差不超过 $2$ 的.
一般这种区间查询都用差分, 求出前 $L - 1$ 个数字和前 $R$ 个数字的答案, 求差即为答案. 设计状态 $f_{i, j, 0/1}$, 其中 $i$ 表示位置, $j$ 表示当前位的数, 第一个 $0/1$ 表示前 $i$ 位是否顶界.
$$
f_{i, j, 0} = f_{i - 1, a_{i - 1}, 1} * [|a_{i - 1} - j| \geq 2, j < a_{i}] + \sum_k^{|k - j| \geq 2} f_{i - 1, k, 0}\\
f_{i, j, 1} = f_{i - 1, a_{i - 1}, 1} * [|a_{i - 1} - j| \geq 2, j = a_{i}]
$$
```cpp
unsigned int a[10005], f[11][11][11], m, n, Cnt(0), A, B, C, D, t, La, Lb, Ansa(0), Ansb(0), Ans(0);
bool b[10005];
char s[10005];
inline void Clr() {
n = RD();
memset(a, 0, sizeof(a));
}
inline unsigned Getlen (unsigned x) {
unsigned tmp(0);
while(x) {
x /= 10;
++tmp;
}
return tmp;
}
inline bool Jdg (const unsigned &x, const unsigned &y) {
if (x < y) {
return y - x > 1;
}
return x - y > 1;
}
void Qry (unsigned &ans, unsigned x, const unsigned &Len) {
if(!x) {
ans = 0;
return;
}
unsigned now(x / Ten[Len - 1]), tmp(11);
for (register unsigned i(1); i < Len; ++i) {//len
for (register unsigned j(1); j < 10; ++j) {//begin
for (register unsigned k(0); k < 10; ++k) {//end
ans += f[i][j][k];//shorter
}
}
}
for (register unsigned i(Len); i >= 1; --i) {//len
now = x / Ten[i - 1];//this number
for (register unsigned j(i == Len ? 1 : 0); (i == 1 ? j <= now : j < now); ++j) {//begin
if(Jdg(j, tmp)) {//last
for (register unsigned k(0); k < 10; ++k) {//end
ans += f[i][j][k];
}
}
}
if(!Jdg(now, tmp)) {
break;
}
x -= Ten[i - 1] * now;
tmp = now;//this num
}
}
int main() {
A = RD() - 1;
La = Getlen(A);
B = RD();
Lb = Getlen(B);
memset(f, 0, sizeof(f));
for (register unsigned i(0); i < 10; ++i) {//begin & end
f[1][i][i] = 1;
}
for (register unsigned i(2); i <= Lb; ++i) {//len
for (register unsigned j(0); j < 10; ++j) {//begin
for (register unsigned k(0); k < 10; ++k) {//end
for (register unsigned i_(0); i_ < 10; ++i_) {//lastend
if (Jdg(i_, k)) {
f[i][j][k] += f[i - 1][j][i_];
}
}
}
}
}
Qry (Ansa, A, La);
Qry (Ansb, B, Lb);
printf("%u\n", Ansb - Ansa);
return Wild_Donkey;
}
```
### [P4317](https://www.luogu.com.cn/problem/P4317)
求 $\prod_{i = 1}^{n} PopCount_i$ 对 $10^7 + 7$ 取模的结果.
设 $Num_i$ 表示 $[1, n]$ 中 $PopCount = i$ 的数的数量, 问题转化为求 $\displaystyle{\prod_i i^{Num_i}}$.
设计状态 $f_{i, j, 0/1}$ 表示到第 $i$ 位, 二进制有 $j$ 个 $1$, 前 $i$ 位是否顶界的数的数量.
$$
f_{i, j, 0} = f_{i - 1, j, 0} + f_{i - 1, j - 1, 0} + f_{i - 1, j, 1} * [a_{i} = 1]\\
f_{i, j, 1} = f_{i - 1, j, 1} * [a_{i} = 0] + f_{i - 1, j - 1, 1} * [a_{i} = 1]\\
Num_i = f_{Len, i, 0} + f_{Len, i, 1}
$$
但是我做题的时候没有想到 DP, 于是用组合数学做了出来. 我们求的是固定了前 $i$ 位, 后面随意组合的所有数对答案的贡献. 如果有 $m - i$ 位是不固定的, 里面有 $j$ 个 $1$, 那么这样的数字就有 $\binom {m - i}{j}$ 种, 如果已固定部分的 PopCount 为 $p$, 则对答案的贡献为 $(j + p)^{\binom {m - i}{j}}
const unsigned long long Mod(10000007);
unsigned long long Ans(1), C[105][105], n;
unsigned m(0), Cnt(0), Tmp(0);
unsigned long long Pow(unsigned long long x, unsigned long long y) {
unsigned long long Pns(1);
while (y) {
if (y & 1) Pns = Pns * x % Mod;
y >>= 1, x = x * x % Mod;
}
return Pns;
}
signed main() {
n = RD();
while (n >> m) ++m; --m;
for (unsigned i(0); i <= m; ++i) {
C[i][0] = 1;
for (unsigned j(1); j <= i; ++j) C[i][j] = C[i - 1][j] + C[i - 1][j - 1];
}
for (unsigned i(m); ~i; --i) {
if (!((n >> i) & 1)) continue;
for (unsigned j(0); j <= i; ++j) {
if (!(j + Cnt)) continue;
Ans = Ans * Pow(j + Cnt, C[i][j]) % Mod;
}
++Cnt;
}
Ans = Ans * Cnt % Mod;
printf("%llu\n", Ans);
return Wild_Donkey;
}
HNOI2002
问题转化为求 [1, n] 中的二进制回文数个数, 注意这里的回文数不能有后缀 0. 设 n 的二进制长度为 m.
由于不能有后缀 0, 所以也不能有前缀 0, 这保证了每个回文数必须以 1 开头, 并以 1 结尾.
我们分为两部分考虑, 先考虑长度为 m 的数, 对于前 \lceil \frac {m}{2} \rceil 位, 只要它们比 n 的前 \lceil \frac {m}{2} \rceil 为小, 那么一定可以存在; 如果大, 那么一定不存在; 如果相等, 则只需要把整个回文数和 n 作比较即可. 因为只要确定了前 \lceil \frac {m}{2} \rceil 位, 就能确定整个回文数, 所以前 \lceil \frac {m}{2} \rceil 位的数量就是长度为 m 的回文数的数量. 这个数量很好算.
接下来考虑长度为 [1, m) 的所有情况, 同样是确定一半的串即可, 这些数加起来便是答案.
unsigned m(0), C, D, t;
unsigned Cnt(0), Ans(0);
char BTT[355][115];
struct Bin {
bitset<355> Nu;
inline Bin() { Nu = 0; }
inline Bin(unsigned x) { Nu = x; }
const inline char operator < (const Bin& x)const {
for (unsigned i(350); ~i; --i) if (Nu[i] ^ x.Nu[i]) return x.Nu[i];
return 0;
}
inline Bin operator << (const unsigned& x) {
Bin New(*this);
New.Nu <<= x;
return New;
}
inline Bin operator >> (const unsigned& x) {
Bin New(*this);
New.Nu >>= x;
return New;
}
inline Bin operator + (const Bin& x) {
Bin New(x);
bitset <355> Tmp(Nu), Tmp2;
while (Tmp.count()) {
Tmp2 = New.Nu & Tmp;
New.Nu ^= Tmp;
Tmp = Tmp2 << 1;
}
return New;
}
inline void operator += (const unsigned& x) {
Bin X(x);
unsigned Tmp(0), Up(0);
for (unsigned i(0); i <= 350; ++i) {
Tmp = Nu[i] + Up + X.Nu[i];
Nu[i] = Tmp & 1;
Up = Tmp >> 1;
}
}
inline void operator += (const Bin& x) {
bitset <355> Tmp(x.Nu), Tmp2;
while (Tmp.count()) {
Tmp2 = Nu & Tmp;
Nu ^= Tmp;
Tmp = Tmp2 << 1;
}
}
inline void operator -= (const unsigned& x) {
Bin X(x);
int Tmp;
unsigned Up(0);
for (unsigned i(0); i <= 350; ++i) {
Tmp = Nu[i] - Up - X.Nu[i];
Up = 0;
while (Tmp < 0) Tmp += 2, ++Up;
Nu[i] = Tmp & 1;
}
}
inline Bin operator * (const unsigned x) {
Bin New;
New.Nu = 0;
for (unsigned i(0); i <= 31; ++i) if (x & (1 << i)) New += ((*this) << i);
return New;
}
inline void operator *= (const unsigned x) {
Bin Tmp(*this);
Nu = 0;
for (unsigned i(0); i <= 31; ++i) if (x & (1 << i)) (*this) += (Tmp << i);
}
inline void RD() {
char rdch[115];
unsigned L(0), R(0);
memset(rdch, 0, sizeof(rdch));
scanf("%s", rdch);
Nu = 0;
while (rdch[L] < '0' || rdch[L] > '9') ++L; R = L;
while (rdch[R] >= '0' && rdch[R] <= '9')++R;
for (unsigned i(L); i < R; ++i) {
(*this) *= 10, (*this) += rdch[i] - '0';
}
}
inline void Print() {
unsigned List[115], Mx(0);
memset(List, 0, sizeof(List));
for (unsigned i(0); i <= 350; ++i) if (Nu[i])
for (unsigned j(0); j <= 110; ++j) List[j] += BTT[i][j];
for (unsigned i(0), Up(0); i <= 110; ++i) {
List[i] = List[i] + Up;
Up = List[i] / 10;
List[i] %= 10;
if (List[i]) Mx = i;
}
for (unsigned i(Mx); ~i; --i) putchar('0' + List[i]);
putchar('\n');
}
}n, A, B;
signed main() {
BTT[0][0] = 1;
for (unsigned i(1); i <= 350; ++i) {
for (unsigned j(0), Up(0); j <= 110; ++j) {
BTT[i][j] = (BTT[i - 1][j] << 1) + Up;
Up = BTT[i][j] / 10;
BTT[i][j] %= 10;
}
}
n.RD();
for (unsigned i(0); i <= 350; ++i) if (n.Nu[i]) m = i;
B = 0, A = n;
for (unsigned i(m >> 1); ~i; --i) A.Nu[i] = A.Nu[m - i];
for (unsigned i(m >> 1); ~i; --i) B.Nu[i] = A.Nu[i + ((m + 1) >> 1)];
B.Nu[m >> 1] = 0;
B += 1;
if (n < A) B -= 1;
A = 0, A.Nu[0] = 1;
for (unsigned i(0); i < m; ++i) {
B += A;
if (i & 1) A.Nu <<= 1;
}
B.Print();
return Wild_Donkey;
}
SCOI2013
给两个 B 进制数 L, R, 分别有 n 和 m 位. 求 [L, R] 每个数的所有子串之和, 用 10 进制表示.
对于本题, 我们规定数位从左到右是从低到高.
状态 f_{i, 1/0} 表示顶界/不顶界的以第 i 为为左边界的后缀中, 所有左边界为 i 的子串之和. 为了辅助转移, 设计 g_{i, 1/0} 表示对应 f 状态表示的所有字串的个数.
考虑如何转移, 我们从任意左边界为 i + 1 的子串前面加一个数字, 得到的就是一个左边界为 i 的子串.
我们把以第 i 位为左边界的不顶界的后缀数量记为 LtR_i, 这个很好求, 用类似快读的方法即可求出. 用 Tmp_i 表示以第 i 为右边界的前缀的数量记为 Tmp_i.
那么转移方程就可以写成:
f_{i, 0} = f_{i + 1, 0}B^2 + \frac{B(B - 1)}{2}(g_{i + 1, 0} + LtR_{i + 1}) + f_{i + 1, 1}a_iB + \frac{a_i(a_i - 1)}{2}(g_{i + 1, 1} + 1)\\
f_{i, 1} = f_{i + 1, 1}B + a_i(g_{i + 1, 1} + 1)\\
g_{i, 0} = g_{i + 1, 0}B + g_{i + 1, 1}a_i + LtR_{i + 1}B + a_i - 1\\
g_{i, 1} = g_{i + 1, 1} + 1
$$
Ans = \sum_{i=1}^{Len}f_{i, 0} * Pow_{i - 1} + f_{i, 1} * Tmp_{i - 1}
$$
用同样的方法算出 $[1, L - 1]$ 的答案, 做差即为所求.
```cpp
const unsigned long long Mod(20130427);
unsigned L[100005], R[100005], n, m;
unsigned long long f[100005][2], g[100005][2], Pow[100005];
unsigned long long Tmp[100005], LtR[100005], Ans(0);
unsigned A, B, C, D, t;
unsigned Cnt(0);
inline unsigned Calc(unsigned x) {
return (((unsigned long long)(x) * (x - 1)) >> 1) % Mod;
}
inline int Do(unsigned* Md, unsigned Len) {
f[Len + 1][1] = f[Len + 1][0] = g[Len + 1][1] = 0;
g[Len + 1][0] = 0;
unsigned long long DRt(0);
LtR[Len + 1] = 0, Tmp[0] = 1;
for (unsigned i(1); i <= Len; ++i) Tmp[i] = (Tmp[i - 1] + Md[i] * Pow[i - 1]) % Mod;
for (unsigned i(Len); i; --i) LtR[i] = (LtR[i + 1] * B + Md[i]) % Mod;
for (unsigned i(Len); i; --i) {
f[i][0] = (((f[i + 1][0] * B % Mod) * B) + Calc(B) * (g[i + 1][0] + LtR[i + 1])) % Mod;
if (Md[i]) f[i][0] = (f[i][0] + (f[i + 1][1] * Md[i] % Mod) * B + Calc(Md[i]) * (g[i + 1][1] + 1)) % Mod;
g[i][0] = (g[i + 1][0] * B + g[i + 1][1] * Md[i] + LtR[i + 1] * B + Md[i] - 1) % Mod;
f[i][1] = (f[i + 1][1] * B + Md[i] * (g[i + 1][1] + 1)) % Mod;
g[i][1] = g[i + 1][1] + 1;
DRt = (DRt + f[i][0] * Pow[i - 1] + f[i][1] * Tmp[i - 1]) % Mod;
}
return DRt % Mod;
}
signed main() {
B = RD(), n = RD(), Pow[0] = 1;
for (unsigned i(1); i <= 100000; ++i) Pow[i] = Pow[i - 1] * B % Mod;
for (unsigned i(n); i; --i) L[i] = RD();
if ((n == 1) && (!(L[1]))) Ans = 0;
else {
for (unsigned i(1); i <= n; ++i) {
if (L[i]) { --L[i];break; }
L[i] = B - 1;
}
if (!L[n]) --n;
Ans = Do(L, n);
}
m = RD();
for (unsigned i(m); i; --i) R[i] = RD();
Ans = Mod + Do(R, m) - Ans;
printf("%llu\n", Ans % Mod);
return Wild_Donkey;
}
```
### 例题
求
$$
\sum_{i = l}^{r} \binom{a+i}{b}c^i \% p
$$
设 $a + i = A_0 + pA_1 + p^2A_2...$, $b = B_0 + pB_1 + p^2B_2...
\binom{a + i}{b} \equiv \prod_{j = 0} \binom{A_j}{B_j} \pmod p
设 i = C_0 + pC_1 + p^2C_2...
c^i \equiv \prod_{j = 0} c^{C_jp^j} \pmod p
问题转化为:
\sum_{i = l}^{r} (\prod_{j = 0} \binom{A_j}{B_j})(\prod_{j = 0} c^{C_j}) \% p
预处理 g_i = c^i \% p.
状态 f_{i, 0/1, 0/1}, 表示到 p 进制第 i 位, 是否顶界, 是否. (转移的条件细节已省略)
f_{i, 0/1, 0/1} = \sum_k f_{i - 1}{0/1'}{0/1'} * \binom{k}{B_i} * g_k
Day24: 期望和概率 DP
NOIP2003
对于一个点带权的二叉树, 定义一颗树的加分为它两个子树加分的乘积加上根节点的权值. 已知中序遍历序列, 求一个前序遍历序列使得整棵树加分最大. 如果答案不唯一则输出任意一个.
中序遍历的一个区间就是一棵子树, 所以将树上问题转化为区间 DP.
$$
f_{i, j} = \max(f_{i, k - 1} * f_{k + 1, j} + a_k)
$$
记录决策即可输出方案.
```cpp
unsigned long long f[33][33], Choi[33][33], Tmp;
unsigned m, n;
unsigned Cnt(0), Ans(0);
inline void DFS(unsigned x, unsigned y) {
if (y < 1) return;
printf("%u ", Choi[x][y]);
unsigned A(Choi[x][y] - x);
DFS(x, A);
DFS(Choi[x][y] + 1, y - A - 1);
}
signed main() {
n = RD();
for (unsigned i(1); i <= n; ++i) f[i][1] = RD(), Choi[i][1] = i, f[i][0] = 1;
for (unsigned Len(2); Len <= n; ++Len) {
for (unsigned i(n - Len + 1); i; --i) {
for (unsigned len(Len - 1); ~len; --len) {
Tmp = f[i][len] * f[i + len + 1][Len - len - 1] + f[i + len][1];
if (f[i][Len] < Tmp) {
f[i][Len] = Tmp, Choi[i][Len] = i + len;
}
}
}
}
printf("%llu\n", f[1][n]);
DFS(1, n);
return Wild_Donkey;
}
```
### [NOIP2008](https://www.luogu.com.cn/problem/P1006)
一个棋盘, 格子带权, 选两条由格子组成的除端点外不相交的路径, 连接左上角和右下角, 使他们的总和最大. 从左上角出发的路径只能朝右或朝下走, 从右下角出发的路径只能朝左或朝上走. 换句话说, 每一步都要使和起点的曼哈顿距离增加 $1$.
为了保证不相交, 我们使两条路径同时走, 这样每次两个路径的端点离起点的曼哈顿距离相等, 就不存在一条路径走到另一条路径曾经走过的位置的情况了. 只要保证两条路径同时走新的一步时不走到同一个格子即可.
设计状态 $f_{i, j, k}$ 表示走了 $i$ 步, 第一条路经走到 $(j, i + 2 - j)$, 第二条路经走到 $(k, i + 2 - k)$ 的最大总和.
$$
f_{i, j, k} = max(f_{i - 1, j, k}, f_{i - 1, j - 1, k}, f_{i - 1, j, k - 1}, f_{i - 1, j - 1, k - 1}) + a_{j, i + 2 - j} + a_{k, i + 2 - k}
$$
$O(n^3)$ 状态, $O(1)$ 转移.
(这个题貌似费用流也可)
远古代码使用的是四维数组的 DP:
```cpp
int n,m,f[55][55][55][55]= {0},a[55][55]= {0}; //不能两次二维过的原因是:第一次保证路径最优并不能使最后的结果最优,所以需要同时考虑两次
int main() {
cin>>n>>m;
for(int i=1; i<=n; i++) for(int j=1; j<=m; j++) cin>>a[i][j];
for(int i=1; i<=n; i++) {
for(int j=1; j<=m; j++) {
for(int k=1; k<=n; k++) {
for(int l=1; l<=m; l++) {
f[i][j][k][l]=max(max(f[i-1][j][k-1][l],f[i-1][j][k][l-1]),max(f[i][j-1][k-1][l],f[i][j-1][k][l-1]));
f[i][j][k][l]+=a[i][j]+a[k][l];
if((i==k)&&(j==l)) { //非法走法
if(((i!=n)||(j!=m))&&((i!=1)||(j!=1))) { //前后两步这样走合法
f[i][j][k][l]=-0x3f3f3f3f;
}
}
}
}
}
}
cout<<f[n][m][n][m]<<endl;
return 0;
}
```
### [NOIP2010](https://www.luogu.com.cn/problem/P1514)
一个棋盘, 每个格子有高度, 第一行每个格子可以建水库, 水可以往相邻的高度严格小于当前格子的格子中流. 判断水是否可以覆盖最后一行所有格子, 如果不能, 求出多少个不能被覆盖, 否则求出在满足覆盖最后一个格子的前提下, 最少建多少个水库.
对于不能完全覆盖的情况, 多源 BFS 就可以判断出答案.
对于可以完全覆盖的情况, 可以结合某些神奇的拓扑学原理, 发现一个输水站覆盖的城市一定是一个连续的区间, 而且对于所有能到覆盖城市的首行的点, 它们的区间左端点关于横坐标单调不降, 右端点也是一样的. 通过记忆化搜索, 求出第一行每个点能覆盖的城市区间, 贪心求解.
复杂度 $O(nm)$.
```cpp
unsigned a[505][505], Range[505][505][2], m, n;
unsigned Q[250005][2], Hd(0), Tl(0);
unsigned List[505][2], NowR(1), Last(0);
unsigned Cnt(0), Ans(0), Tmp(0);
char Ava[505][505];
inline void Merge(unsigned Fx, unsigned Fy, unsigned Tx, unsigned Ty) {
if (Range[Fx][Fy][0] > m) return;
Range[Tx][Ty][0] = min(Range[Tx][Ty][0], Range[Fx][Fy][0]);
Range[Tx][Ty][1] = max(Range[Tx][Ty][1], Range[Fx][Fy][1]);
}
inline void DFS(unsigned x, unsigned y) {
if (Range[x][y][0]) return;
if (x == n) Range[x][y][0] = Range[x][y][1] = y;
else Range[x][y][0] = 0x3f3f3f3f;
if ((x < n) && (a[x + 1][y] < a[x][y])) DFS(x + 1, y), Merge(x + 1, y, x, y);
if ((x > 1) && (a[x - 1][y] < a[x][y])) DFS(x - 1, y), Merge(x - 1, y, x, y);
if ((y < m) && (a[x][y + 1] < a[x][y])) DFS(x, y + 1), Merge(x, y + 1, x, y);
if ((y > 1) && (a[x][y - 1] < a[x][y])) DFS(x, y - 1), Merge(x, y - 1, x, y);
}
signed main() {
n = RD(), m = RD();
for (unsigned i(1); i <= n; ++i) for (unsigned j(1); j <= m; ++j) a[i][j] = RD();
for (unsigned i(1); i <= m; ++i) Q[++Tl][0] = 1, Q[Tl][1] = i, Ava[1][i] = 1;
while (Hd ^ Tl) {
unsigned Curx(Q[++Hd][0]), Cury(Q[Hd][1]);
if ((Curx > 1) && (!Ava[Curx - 1][Cury]) && (a[Curx - 1][Cury] < a[Curx][Cury]))
Ava[Curx - 1][Cury] = 1, Q[++Tl][0] = Curx - 1, Q[Tl][1] = Cury;
if ((Curx < n) && (!Ava[Curx + 1][Cury]) && (a[Curx + 1][Cury] < a[Curx][Cury]))
Ava[Curx + 1][Cury] = 1, Q[++Tl][0] = Curx + 1, Q[Tl][1] = Cury;
if ((Cury > 1) && (!Ava[Curx][Cury - 1]) && (a[Curx][Cury - 1] < a[Curx][Cury]))
Ava[Curx][Cury - 1] = 1, Q[++Tl][0] = Curx, Q[Tl][1] = Cury - 1;
if ((Cury < m) && (!Ava[Curx][Cury + 1]) && (a[Curx][Cury + 1] < a[Curx][Cury]))
Ava[Curx][Cury + 1] = 1, Q[++Tl][0] = Curx, Q[Tl][1] = Cury + 1;
}
for (unsigned i(1); i <= m; ++i) Ans += Ava[n][i];
if (Ans < m) {
printf("0\n%u\n", m - Ans);
return 0;
}
for (unsigned i(1); i <= m; ++i) {
DFS(1, i);
if (Range[1][i][0] < m) List[++Cnt][0] = Range[1][i][0], List[Cnt][1] = Range[1][i][1];
}
Ans = 0;
for (unsigned i(1); i <= Cnt; ++i) {
if (NowR < List[i][0]) NowR = Last + 1, Last = 0, ++Ans;
Last = max(Last, List[i][1]);
}
if (NowR <= m) ++Ans;
printf("1\n%u\n", Ans);
return Wild_Donkey;
}
```
### [ZJOI2006](https://www.luogu.com.cn/problem/P2585)
给一个二叉树序列, $0$ 表示叶子, $1$ 表示只有一个儿子的节点, 后面紧跟着的合法序列是它子树的序列, $2$ 表示有两个儿子的节点, 后面紧跟着两个合法序列是它两个子树的序列. 需要给这个二叉树染上 RGB, 保证一个节点和自己的父亲和兄弟不同色, 问这棵树最多/最少有多少个点是绿色.
这个题第一个难点是根据二叉树序列建树, 本来想的是用链表加迭代建树, 因为懒得写又思考了一下发现可以堆栈建树.
节点 $i$ 存 $f_{i, 0/1/2}$ 表示当前节点选红/绿/蓝的最多绿色数量, $g_{i, 0/1/2}$ 存最少绿色数量.
对于叶子 $i$.
$$
g_{i, 0} = f_{i, 0} = 0\\
g_{i, 1} = f_{i, 1} = 1\\
g_{i, 2} = f_{i, 2} = 0
$$
对于只有一个儿子的节点 $i$.
$$
f_{i, 0} = max(f_{Son_i, 1}, f_{Son_i, 2})\\
f_{i, 1} = max(f_{Son_i, 0}, f_{Son_i, 2}) + 1\\
f_{i, 2} = max(f_{Son_i, 0}, f_{Son_i, 1})\\
g_{i, 0} = min(f_{Son_i, 1}, f_{Son_i, 2})\\
g_{i, 1} = min(f_{Son_i, 0}, f_{Son_i, 2}) + 1\\
g_{i, 2} = min(f_{Son_i, 0}, f_{Son_i, 1})
$$
对于有两个儿子的 $i$.
$$
f_{i, 0} = max(f_{LS_i, 1} + f_{RS_i, 2}, f_{RS_i, 1} + f_{LS_i, 2})\\
f_{i, 1} = max(f_{LS_i, 0} + f_{RS_i, 2}, f_{RS_i, 0} + f_{LS_i, 2}) + 1\\
f_{i, 2} = max(f_{LS_i, 0} + f_{RS_i, 1}, f_{RS_i, 0} + f_{LS_i, 1})\\
g_{i, 0} = min(f_{LS_i, 1} + f_{RS_i, 2}, f_{RS_i, 1} + f_{LS_i, 2})\\
g_{i, 1} = min(f_{LS_i, 0} + f_{RS_i, 2}, f_{RS_i, 0} + f_{LS_i, 2}) + 1\\
g_{i, 2} = min(f_{LS_i, 0} + f_{RS_i, 1}, f_{RS_i, 0} + f_{LS_i, 1})\\
$$
对于本题, 蓝色和红色显然等价, 所以可以少 DP 一个 $f_{i, 2}$ 和 $g_{i, 2}$.
```cpp
unsigned m, n, Stack[500005], Head(0);
unsigned A, B, C, D, t;
unsigned Cnt(0), Ans(0), Tmp(0);
char a[500005];
struct Node {
Node* LS, * RS;
unsigned f[2], g[2];
inline void Add(Node* x) {
if (LS) RS = x;
else LS = x;
}
inline void DFS() {
if (!LS) {
g[0] = f[0] = 1, g[1] = f[1] = 0;
return;
}
LS->DFS();
if (!RS) {
f[0] = LS->f[1] + 1;
f[1] = max(LS->f[0], LS->f[1]);
g[0] = LS->g[1] + 1;
g[1] = min(LS->g[0], LS->g[1]);
return;
}
RS->DFS();
f[0] = LS->f[1] + RS->f[1] + 1;
f[1] = max(LS->f[0] + RS->f[1], LS->f[1] + RS->f[0]);
g[0] = LS->g[1] + RS->g[1] + 1;
g[1] = min(LS->g[0] + RS->g[1], LS->g[1] + RS->g[0]);
}
}N[500005];
signed main() {
scanf("%s", a + 1);
n = strlen(a + 1), Stack[++Head] = 1;
for (unsigned i(2); i <= n; ++i) {
N[Stack[Head]].Add(N + i), --a[Stack[Head]];
while (Head && (a[Stack[Head]] <= '0')) --Head;
if (a[i] > '0') Stack[++Head] = i;
}
N[1].DFS();
printf("%u %u\n", max(N[1].f[0], N[1].f[1]), min(N[1].g[0], N[1].g[1]));
return Wild_Donkey;
}
```
### [NOIP2016](https://www.luogu.com.cn/problem/P1850)
一个学校有不多于 $300$ 个教室, 所有教室连通, 一共 $n$ 节课, 每节课原教室 $a_i$ 和备用教室 $b_i$, 上完第 $i$ 节课需要花费最短路的代价从第 $i$ 节实际上课教室到第 $i + 1$ 节实际上课教室, 每节课可以选择申请从原教室换到备用教室, 成功率 $p_i$. 最多对 $m$ 节课申请, 求期望最小交通代价.
预处理全源最短路, 设计状态 $f_{i, j, 0/1}$, 表示考虑了 $i$ 节课, 申请了 $j$ 节课, $0/1$ 表示第 $i$ 节是否申请.
$$
f_{i, j, 0} = min(f_{i - 1, j, 0} + Dis_{c_{i - 1}, c_i}, f_{i - 1, j, 1} + (1 - k_{i - 1}) * Dis_{c_{i - 1}, c_i} + k_{i - 1} * Dis_{d_{i - 1}, c_i})\\
f_{i, j, 1} = min(f_{i - 1, j - 1, 0} + (1 - k_i) * Dis_{c_{i - 1}, c_i} + k_i * Dis_{c_{i - 1}, d_i},\\
f_{i - 1, j - 1, 1} + (1 - k_{i - 1})(1 - k_i) * Dis_{c_{i - 1}, c_i} + k_{i - 1}(1 - k_i) * Dis_{d_{i - 1}, c_i} +\\
(1 - k_{i - 1})k_i * Dis_{d_{i - 1}, c_i} + k_{i - 1}k_i * Dis_{d_{i - 1}, d_i})
$$
答案即为 $min(f_{n, i, 0}, f_{n, i, 1})$, 因为 $m$ 只是上限, 而不一定申请越多越有利.
```cpp
double p[2005], f[2005][2], g[2], Ans(1000000000);
unsigned m, n, Cn, Ce;
unsigned Dis[305][305];
unsigned a[2005], b[2005];
unsigned A, B, C, D, t;
unsigned Cnt(0), Tmp(0);
signed main() {
n = RD(), m = RD(), Cn = RD(), Ce = RD();
for (unsigned i(1); i <= n; ++i) a[i] = RD();
for (unsigned i(1); i <= n; ++i) b[i] = RD();
for (unsigned i(1); i <= n; ++i) scanf("%lf", p + i);
memset(Dis, 0x3f, sizeof(Dis));
for (unsigned i(1); i <= Ce; ++i) {
A = RD(), B = RD();
Dis[A][B] = Dis[B][A] = min(Dis[A][B], RD());
}
for (unsigned i(1); i <= Cn; ++i) Dis[i][i] = 0;
for (unsigned i(1); i <= Cn; ++i) for (unsigned j(1); j <= Cn; ++j)
for (unsigned k(1); k <= Cn; ++k) Dis[j][k] = min(Dis[j][i] + Dis[i][k], Dis[j][k]);
for (unsigned i(0); i <= m; ++i) f[i][0] = f[i][1] = 1000000000;
f[0][0] = 0, f[1][1] = 0;
for (unsigned i(2); i <= n; ++i) {
for (unsigned j(min(m, i)); j; --j) {
g[0] = min(f[j][0] + Dis[a[i]][a[i - 1]],
f[j][1] + Dis[a[i]][b[i - 1]] * p[i - 1] + Dis[a[i]][a[i - 1]] * (1 - p[i - 1]));
g[1] = min(f[j - 1][0] + Dis[b[i]][a[i - 1]] * p[i] + Dis[a[i]][a[i - 1]] * (1 - p[i]),
f[j - 1][1] + Dis[b[i]][b[i - 1]] * p[i] * p[i - 1] + Dis[a[i]][b[i - 1]] * (1 - p[i]) * p[i - 1] +
Dis[b[i]][a[i - 1]] * p[i] * (1 - p[i - 1]) + Dis[a[i]][a[i - 1]] * (1 - p[i]) * (1 - p[i - 1]));
f[j][0] = g[0], f[j][1] = g[1];
}
f[0][0] = f[0][0] + Dis[a[i]][a[i - 1]];
}
for (unsigned i(0); i <= m; ++i) {
Ans = min(Ans, min(f[i][0], f[i][1]));
}
printf("%.2lf", Ans);
return Wild_Donkey;
}
```
### [NOIP2014](https://www.luogu.com.cn/problem/P1941)
模拟 Flappy Bird, 中间读错几次题, 不过还是改过来了. 一个 $n$ 长度的局面, 高度为 $m$, 有 $t$ 个障碍, 每个障碍允许 $(Dw_i, Up_i)$ 高度 (开区间) 通过. (每个位置最多有 $1$ 个障碍, 障碍不按坐标顺序给出, 务必记得排序)
可以选择位置 $0$ 的任意高度出发, 到达位置 $n$ 的任意高度成功. 每个单位时间向右移动一个单位, 从位置 $i - 1$ 到位置 $i$ 的时候, 不操作会使高度下降 $Fl_i$, 操作 $k > 0$ 次会使高度上升 $Ri_ik$ 次. $m$ 高度有天花板, 再怎么操作到更高的地方, 高度都变回 $m$. 高度如果 $\leq 0$ 则失败.
如果有操作方式可以通过, 求最少操作次数, 否则求最多经过多少个障碍.
设计状态 $f_{i, j}$ 为走到第 $i$ 列, 高度为 $j$ 的最少操作数. 一般很容易想到枚举操作次数 $O(m)$ 转移, 可是这样的复杂度是 $O(nm^2)$.
我们可以先考虑操作数量 $\geq 0$ 的转移, 这样的转移可以直接前缀和优化 (注意顺序, $j$ 从小到大枚举):
$$
f_{i, j} = min(f_{i - 1, j - Ri_i} + 1, f_{i, j - Ri_i} + 1)
$$
对于 $m$ 的天花板需要特判:
$$
f_{i, m} = min(f_{i - 1, m - j} + 1) (j \leq Ri_i)
$$
然后考虑不操作, 自由落体的转移:
$$
f_{i, j} = min(f_{i, j}, f_{i - 1, j + Fl_i})
$$
如果本位置有障碍, 把不能通过的位置的值都设为无穷大, 并且每个障碍都判断是否还有机会通过, 一旦提前结束, 及时输出返回. 最后输出前也要判断是否能到达终点.
这样就实现了 $O(nm)$ 状态, 每 $O(m)$ 个状态一起 $O(m)$ 转移. 时间复杂度 $O(nm)$, 空间复杂度 $O(nm)$, 滚动数组优化空间到 $O(m + n)$.
```cpp
unsigned f[1005], g[1005], m, n;
unsigned Ri[10005], Fl[10005];
unsigned A, B, C, D, t;
unsigned Cnt(1), Ans(0x3f3f3f3f), Tmp(0);
struct Col {
unsigned Pos, Dw, Up;
inline const char operator < (const Col& x) const {
return this->Pos < x.Pos;
}
}No[10005];
signed main() {
n = RD(), m = RD(), t = RD();
for (unsigned i(1); i <= n; ++i) Ri[i] = RD(), Fl[i] = RD();
for (unsigned i(1); i <= t; ++i) No[i].Pos = RD(), No[i].Dw = RD(), No[i].Up = RD();
sort(No + 1, No + t + 1);
for (unsigned i(1); i <= n; ++i) {
memset(g, 0x3f, sizeof(g));
for (unsigned j(m - Ri[i] + 1); j <= m; ++j) g[m] = min(g[m], f[j] + 1);
for (unsigned j(m - Ri[i]); j; --j) g[j + Ri[i]] = min(g[j + Ri[i]], f[j] + 1);
for (unsigned j(Ri[i] + 1); j <= m; ++j) g[j] = min(g[j], g[j - Ri[i]] + 1);
for (unsigned j(m - Ri[i] + 1); j <= m; ++j) g[m] = min(g[m], g[j] + 1);
for (unsigned j(Fl[i] + 1); j <= m; ++j) g[j - Fl[i]] = min(g[j - Fl[i]], f[j]);
if (No[Cnt].Pos == i) {
Ans = 0x3f3f3f3f, memset(f, 0x3f, sizeof(f));
for (unsigned j(No[Cnt].Dw + 1); j < No[Cnt].Up; ++j) Ans = min(Ans, f[j] = g[j]);
if (Ans >= 0x3f3f3f3f) {
printf("0\n%u\n", Cnt - 1);
return 0;
}
Cnt++;
}
else memcpy(f, g, sizeof(f));
}
Ans = 0x3f3f3f3f;
for (unsigned j(1); j <= m; ++j) Ans = min(Ans, g[j]);
if (Ans < 0x3f3f3f3f) printf("1\n%u\n", Ans);
else printf("0\n%u\n", Cnt);
return Wild_Donkey;
}
```
### [CSP2019](https://www.luogu.com.cn/problem/P5664)
有 $n$ 个烹饪方式, $m$ 种食材, 第 $i$ 中烹饪方式可以用第 $j$ 种食材做 $a_{i, j}$ 道菜. 要求做 $p$ 道菜, 它们所用烹饪方式互不相同, 每种食材最多做 $\lfloor \frac p2 \rfloor$ 道菜. 求总方案数.
计数圣经: 合法方案数 = 总方案数 - 不合法方案数
如果不考虑 $\lfloor \frac p2 \rfloor$ 的限制, 总方案数很好求. 定义数组 $g_i$ 作为一种方法做的所有菜, 这样每种方法的情况就只有 $g_i + 1$ 种, 做菜有 $g_i$ 种情况, 不做有 $1$ 种.
$$
g_{i} = \sum_{j = 1}^{m} a_{i, j}
$$
总方案数可以表示为 (最后 $-1$ 是排除掉什么也没做的情况):
$$
(\prod_{i = 1}^{i \leq n} (g_i + 1)) - 1
$$
因为每个不合法的方案中, 出现次数大于等于做菜数量一半的食材 $x$ 是确定的, 所以我们可以根据 $x$ 的不同将不合法的方案分类. 枚举 $x$, 每次跑一遍 DP 求出它出现多于 $\lfloor \frac p2 \rfloor$ 的方案数.
假设现在需要求 $x$ 出现次数比 $\lfloor \frac p2 \rfloor$ 大的方案数, 设计状态 $f_{i, j, k}$ 表示考虑了前 $i$ 种方式, 用 $x$ 做了 $j$ 道菜, 用别的食材做了 $k$ 道菜的情况.
$$
f_{i, j, k} = f_{i - 1, j, k} + f_{i - 1, j - 1, k} * a_{i, x} + f_{i - 1, j, k - 1} * (g_i - a_{i, x})
$$
最后 $x$ 作为出现最多的食材的不合法方案数即为:
$$
\sum_{i > j} f_{n, i, j}
$$
状态数 $O(n^3)$, 转移 $O(1)$, 跑 $m$ 遍, 总复杂度 $O(n^3m)$, 可以得到 $84'$.
接下来考虑优化, 设 $f_{i, j}$ 表示考虑前 $i$ 种方法, 第 $x$ 种食材出现次数比其它的食材出现次数总和多 $j - n$ 的方案数.
$$
f_{i, j} = f_{i - 1, j} + f_{i - 1, j - 1} * a_{i, x} + f_{i - 1, j + 1} * (g_i - a_{i, x})
$$
$x$ 作为出现最多的食材的不合法方案数就变成:
$$
\sum_{i > n} f_{n, i}
$$
状态 $O(n^2)$, 转移 $O(1)$, 做 $O(m)$ 次, 时间复杂度 $O(n^2m)$, 可滚动数组到一维, 但是输入已经是 $O(nm)$, 滚动只是为了炫技.
```cpp
unsigned long long Mod(998244353);
unsigned long long Ans(1), f[205], t[205];
unsigned a[105][2005], m, n;
unsigned A, B, C, D;
unsigned Cnt(0), Tmp(0);
signed main() {
n = RD(), m = RD();
for (unsigned i(1); i <= n; ++i) {
for (unsigned j(1); j <= m; ++j) {
a[i][0] += (a[i][j] = RD());
if (a[i][0] >= Mod) a[i][0] -= Mod;
}
Ans = Ans * (a[i][0] + 1) % Mod;
}
for (unsigned i(1); i <= m; ++i) {
memset(f, 0, sizeof(f)), memset(t, 0, sizeof(t)), t[101] = 1;
for (unsigned j(1); j <= n; ++j) {
for (unsigned k(101 - j); k <= j + 101; ++k)
f[k] = (t[k] + t[k - 1] * a[j][i] + t[k + 1] * (Mod + a[j][0] - a[j][i])) % Mod;
memcpy(t, f, sizeof(t));
}
for (unsigned j(n + 101); j > 101; --j) Ans = Mod + Ans - t[j];
}
--Ans, Ans %= Mod;
printf("%llu\n", Ans);
return Wild_Donkey;
}
```
### [COCI2019](https://www.luogu.com.cn/problem/P5307)
给一个 $n * m$ 的棋盘, 每个格子有权值. 求从左上角到右下角, 格子乘积大于等于 $t$ 的路径数量.
第一眼想到的是直接 DP, $f_{i, j, k}$, 表示这个点取 $k$ 为乘积的路径数, 空间复杂度 $O(nmt)$ 这样需要开 $300*300*10^6$ 的数组, 这显然是开不下的. 我们滚动数组可以将空间卡到 $O(mt)$, 但是时间 $O(nmt)$ 仍然无法承受.
先假设下面的式子成立.
$\lfloor \frac{ \lfloor \frac{n}{a} \rfloor}{b} \rfloor = \lfloor \frac{n}{ab} \rfloor$.
那么就可以将问题转化为以 $t - 1$ 为被除数, 从头开始用路径上的数去除, 到最后除到 $0$ 的路径数量. 因为只有 $\geq t$ 的数字 $x$ 满足 $\lfloor \frac (t - 1)x \rfloor = 0$. 而如果这样, 我们最后一维的实际可能的状态就会变成所有 $t - 1$ 为被除数的带余除法的可能出现的商, 这个数量级是 $O(\sqrt t)$ 的.
然后对前面的假设进行证明, 假设 $n = ak_1 + q_1$, $k_1 = bk_2 + q_2$.
所以 $n = a(bk_2 + q_2) + q_1 = abk_2 + aq_2 + q_1$. 因为 $q_2 < b$, 所以 $aq_2 \leq ab - a$, 又因为 $q_1 < a$, 所以 $aq_2 + q_1 < ab$.
所以 $\lfloor \frac n{ab} \rfloor = k_2 = \lfloor \frac{ \lfloor \frac{n}{a} \rfloor}{b} \rfloor
这样最后一维就变成了 O(\sqrt t), 回顾一下状态, f_{i, j, k} 表示从 (1, 1) 到 (i, j) 的路径中, t - 1 除以路径上格子乘积的结果为 k 的路径数. 我们接下来需要做的就是把较为离散的 k 约束到很小的值域内即可.
unordered_map 显然可以完成这个工作, 不过需要滚动数组:
const unsigned long long Mod(1000000007);
unordered_map <unsigned, unsigned> f[2][305];
unsigned long long C[605][605], Ans(0);
unsigned a[305][305], m, n;
unsigned A, B, D, t;
unsigned Cnt(0), Tmp(0);
signed main() {
n = RD(), m = RD(), t = RD() - 1;
for (unsigned i(1); i <= n; ++i) for (unsigned j(1); j <= m; ++j) a[i][j] = RD();
for (unsigned i(0); i <= 600; ++i) {
C[i][0] = 1;
for (unsigned j(1); j <= i; ++j) {
C[i][j] = C[i - 1][j] + C[i - 1][j - 1];
if (C[i][j] >= Mod) C[i][j] -= Mod;
}
}
if (a[1][1] > t) { printf("%llu\n", C[n + m - 2][n - 1]); return 0; }
else f[1][1][t / a[1][1]] = 1;
for (unsigned i(1); i < n; ++i) {
for (unsigned j(1); j < m; ++j) {
for (auto k : f[i & 1][j]) {
unsigned Nu(k.first), Cas(k.second);
if (a[i + 1][j] > Nu)
Ans = (Ans + Cas * C[n + m - i - j - 1][n - i - 1]) % Mod;
else {
unsigned Des(Nu / a[i + 1][j]);
f[(i & 1) ^ 1][j][Des] += Cas;
if (f[(i & 1) ^ 1][j][Des] >= Mod) f[(i & 1) ^ 1][j][Des] -= Mod;
}
if (a[i][j + 1] > Nu)
Ans = (Ans + Cas * C[n + m - i - j - 1][n - i]) % Mod;
else {
unsigned Des(Nu / a[i][j + 1]);
f[i & 1][j + 1][Des] += Cas;
if (f[i & 1][j + 1][Des] >= Mod) f[i & 1][j + 1][Des] -= Mod;
}
}
f[i & 1][j].clear();
}
for (auto k : f[i & 1][m]) {
unsigned Nu(k.first), Cas(k.second);
if (a[i + 1][m] > Nu) { Ans += Cas;if (Ans >= Mod) Ans -= Mod; }
else {
unsigned Des(Nu / a[i + 1][m]);
f[(i & 1) ^ 1][m][Des] += Cas;
if (f[(i & 1) ^ 1][m][Des] >= Mod) f[(i & 1) ^ 1][m][Des] -= Mod;
}
}
f[i & 1][m].clear();
}
for (unsigned j(1); j < m; ++j) for (auto k : f[n & 1][j]) {
unsigned Nu(k.first), Cas(k.second);
if (a[n][j + 1] > Nu) {
Ans += Cas;
if (Ans >= Mod) Ans -= Mod;
}
else {
unsigned Des(Nu / a[n][j + 1]);
f[n & 1][j + 1][Des] += Cas;
if (f[n & 1][j + 1][Des] >= Mod) f[n & 1][j + 1][Des] -= Mod;
}
}
printf("%llu\n", Ans);
return Wild_Donkey;
}
stl 的效率真是让人不敢恭维, 所以这份代码只能拿到 50', 即使开 -O2, 也只能拿到 70'. 只能手写映射.
const unsigned long long Mod(1000000007);
unsigned List[1000005], Back[2005], f[2][305][2005];
unsigned long long C[605][605], Ans(0);
unsigned a[305][305], m, n;
unsigned A, B, D, t;
unsigned Cnt(0), Tmp(0);
signed main() {
n = RD(), m = RD(), t = RD() - 1;
for (unsigned i(1); i <= t; ++i) if (!List[t / i]) Back[List[t / i] = ++Cnt] = t / i;
for (unsigned i(1); i <= n; ++i) for (unsigned j(1); j <= m; ++j) a[i][j] = RD();
for (unsigned i(0); i <= 600; ++i) {
C[i][0] = 1;
for (unsigned j(1); j <= i; ++j) {
C[i][j] = C[i - 1][j] + C[i - 1][j - 1];
if (C[i][j] >= Mod) C[i][j] -= Mod;
}
}
if (a[1][1] > t) { printf("%llu\n", C[n + m - 2][n - 1]); return 0; }
else f[1][1][List[t / a[1][1]]] = 1;
for (unsigned i(1); i < n; ++i) {
for (unsigned j(1); j < m; ++j) {
for (unsigned k(1); k <= Cnt; ++k) if (f[i & 1][j][k]) {
unsigned Nu(Back[k]), Cas(f[i & 1][j][k]);
if (a[i + 1][j] > Nu)
Ans = (Ans + Cas * C[n + m - i - j - 1][n - i - 1]) % Mod;
else {
unsigned Des(List[Nu / a[i + 1][j]]);
f[(i & 1) ^ 1][j][Des] += Cas;
if (f[(i & 1) ^ 1][j][Des] >= Mod) f[(i & 1) ^ 1][j][Des] -= Mod;
}
if (a[i][j + 1] > Nu)
Ans = (Ans + Cas * C[n + m - i - j - 1][n - i]) % Mod;
else {
unsigned Des(List[Nu / a[i][j + 1]]);
f[i & 1][j + 1][Des] += Cas;
if (f[i & 1][j + 1][Des] >= Mod) f[i & 1][j + 1][Des] -= Mod;
}
}
memset(f[i & 1][j], 0, (Cnt + 1) << 2);
}
for (unsigned k(1); k <= Cnt; ++k) if (f[i & 1][m][k]) {
unsigned Nu(Back[k]), Cas(f[i & 1][m][k]);
if (a[i + 1][m] > Nu) { Ans += Cas;if (Ans >= Mod) Ans -= Mod; }
else {
unsigned Des(List[Nu / a[i + 1][m]]);
f[(i & 1) ^ 1][m][Des] += Cas;
if (f[(i & 1) ^ 1][m][Des] >= Mod) f[(i & 1) ^ 1][m][Des] -= Mod;
}
}
memset(f[i & 1][m], 0, (Cnt + 1) << 2);
}
for (unsigned j(1); j < m; ++j)for (unsigned k(1); k <= Cnt; ++k) if (f[n & 1][j][k]) {
unsigned Nu(Back[k]), Cas(f[n & 1][j][k]);
if (a[n][j + 1] > Nu) {
Ans += Cas;
if (Ans >= Mod) Ans -= Mod;
}
else {
unsigned Des(List[Nu / a[n][j + 1]]);
f[n & 1][j + 1][Des] += Cas;
if (f[n & 1][j + 1][Des] >= Mod) f[n & 1][j + 1][Des] -= Mod;
}
}
printf("%llu\n", Ans);
return Wild_Donkey;
}
HNOI2007
有 n 个物品和容量 m 的背包, 每个物品的体积可以用 a_i2^{b_i} 来表示 a_i \leq 10, 求最大价值.
将物品按 b 排序, 从小到大考虑, 每次容量最多是 O(a_in) \approx 1000, 做 0/1 背包.
每次 b 增加, 将背包容量倍增, 数组下标除以 2, 丢弃零头.
因为每次做背包容量为 1000, 物品共 100 种, 做 30 次, 所以总复杂度约为 10^7.
虽然课是这么听的, 然而, 实际回过头来补题的时候我却是按 b 从大到小考虑的. 因为人的直觉都是先放大的再放小的啊.
仍然是按 b 给物品排序, 从大到小. 设计状态 f_{i, j} 表示只考虑 b \geq i, 还剩至少 2^ij 容量的最多价值. 转移有两种:
f_{i, 2j + (\lfloor \frac m{2^i} \rfloor \And 1)} = max(f_{i, 2j + (\lfloor \frac m{2^i} \rfloor \And 1)}, f_{i + 1, j})
f_{i, j} = max(f_{i, j}, f_{i, j + a_x} + v_x)
注意是 0/1 背包, 所以第二种转移的 j 要从小到大枚举.
状态 O((n + \max b) n \max a), 转移 O(1), 复杂度 O((n + \max b) n \max a).
int f[35][1005], Ans;
unsigned a[10005], m, n;
unsigned A, B, C, D, t;
unsigned Cnt(0), Tmp(0);
struct Orb {
int Val;
unsigned Wei, Bi;
const inline char operator < (const Orb& x) const {
return (Bi ^ x.Bi) ? (Bi > x.Bi) : (Val < x.Val);
}
}O[105];
inline void Clr() {
memset(f, 0xaf, sizeof(f)), Ans = 0;
}
signed main() {
for (;; ) {
Clr();
n = RDsg(), m = RD();
if (n > 0x3f3f3f3f) break;
for (unsigned i(1); i <= n; ++i) {
O[i].Wei = RD(), O[i].Val = RD(), O[i].Bi = 0;
if (!O[i].Wei) A += O[i].Val, O[i].Bi = O[i].Val = 0;
while (!(O[i].Wei & 1)) O[i].Wei >>= 1, ++(O[i].Bi);
}
sort(O + 1, O + n + 1), f[30][m & (1 << 30)] = f[30][0] = 0;
for (unsigned i(30), j(1); j <= n; ++j) {
while (i > O[j].Bi) {
for (unsigned k(1000); ~k; --k) {
unsigned Des((k << 1) + ((m >> (i - 1)) & 1));
if (Des > 1000) f[i - 1][1000] = max(f[i - 1][1000], f[i][k]);
else f[i - 1][Des] = max(f[i - 1][Des], f[i][k]);
}
--i;
for (unsigned k(1000); ~k; --k) f[i][k] = max(f[i][k], f[i][k + 1]);
}
for (unsigned k(0); k + O[j].Wei <= 1000; ++k) {
if (f[i][k + O[j].Wei] >= 0)
f[i][k] = max(f[i][k], f[i][k + O[j].Wei] + O[j].Val);
}
Ans = max(Ans, f[i][0]);
}
printf("%d\n", Ans + A);
}
return Wild_Donkey;
}
NOI2020
给 n 种食材, 每种质量 a_i, 做 m 道菜, 每道菜质量 c. 每道菜最多由两种食材做成, 求一个可行方案. 保证 m \geq n - 2.
首先先找一个可以应对一切 m \geq n - 1 的策略.
我们发现, 对于一个 m = n - 1 的局面, m + 1 种食材要组成 m 个 c 的菜, 质量最小的食材必须不足 c, 否则这 m + 1 种食材的质量一定大于 (m + 1)c. 我们只要把最少的食材用光, 然后用最大的食材来补充剩余部分即可. 食材减少了一种, 需要做的菜减少了一种, 这时的问题还会是 m = n - 1 的局面. 直到 m = 1 = n - 1 时, 剩下两种食材组成一道菜即可.
如果一开始 m \geq n, 那么 m 至少是 n, 所以最多的食材至少是 c, 我们用最多的食材本身做一道菜, 就可以把 m 减少而 n 不变, 迟早可以得到 m = n - 1 的局面.
只剩下 m = n - 2 的情况无法解决了. 我们发现如果能够把问题分成两半, 使得两个子问题都是 m = n - 1 的情况, 分别求解然后合并即可. 这样确实可以找到一些问题的解, 但是如何说明这样可以找到所有存在解的局面的解, 而不会漏掉任何存在解的局面呢?
我们把 m 道菜分成 2m 个部分. 这 2m 个部分可以根据食材染色. 如果把有相同颜色的菜之间连边, 可以得到一个图. 对于 m 个单点, 我们连 x 条边, 图中最少有 m - x 个连通块. 一个局面不能被分成两个互不影响的子问题, 且存在解的情况, 相当于根据颜色连边后, 这 m 个单点可以连成一个连通块. 但是 2m 个部分, 每种颜色至少出现一次, 那么还剩下 2m - (m + 2) 个格子可以自由填入, 也就是 m - 2 个. 即使我们每次填入都可以连接两个连通块 (这也是能做到的最优的结果), 那么最后最少可以得到 2 个连通块, 无法做到 m 个点都联通. 因此不存在 m = n - 2 的有解情况不可以被分成两个独立的子问题.
接下来只要考虑如何分成两个独立子问题即可. 我们需要从 n 种食材中, 任选 x 个使得它们的质量和为 (x - 1)c.
设计状态 f_{i, j, k} 表示前 i 种食材选出一个大小为 j 子集使得质量和为 k 的可行性. 状态 O(n^3m), 转移 O(1), 复杂度 O(n^3m).
重新审视我们的问题, 选 x 种食材, 使得 \sum_{i} a_i = (x - 1)c. 把式子进行变形, \sum_{i} c - a_i = c. 这样就能把状态压到 f_{i, j}, 表示前 i 种食材选出 x 子集, 满足 \sum_i c - a_i = j. 这样就把状态优化到了 O(n^2m).
f_{i, j} = f_{i - 1, j} | f_{i - 1, j - c + a_i}
不过这样仍然是过不了的, 因为状态只有 0/1 之分, 而且通过位运算转移, 所以可以用 bitset 优化到 O(\frac{n^2m}{64}).
f_{i} = f_{i - 1} | (f_{i - 1} << (c - a_i))
const unsigned Mi(2500001);
multiset<pair<unsigned, unsigned> > S;
bitset<5000005> f[505];
int b[505];
unsigned a[505], m, n, c;
unsigned A, B, C, D, t;
unsigned Cnt(0), Tmp(0);
char Flg(0);
inline void Clr() {
Flg = 0;
}
inline void Roll(unsigned x) {
S.clear();
unsigned Now(Mi + c);
for (unsigned i(x); i; --i) {
if (f[i - 1][Now]) continue;
S.insert(make_pair(a[i], i)), Now -= b[i], a[i] = 0x3f3f3f3f;
}
}
inline void Do(unsigned x) {
for (unsigned i(1); i <= x; ++i) {
unsigned Num((S.begin())->second), Now((S.begin())->first);
S.erase(S.begin());
if (Now < c) {
// printf("Size %u\n", S.size());
unsigned Snu((--(S.end()))->second), Sno((--(S.end()))->first);
S.erase(--(S.end()));
printf("%u %u %u %u\n", Num, Now, Snu, c - Now);
if (Sno + Now > c) S.insert(make_pair(Sno + Now - c, Snu));
}
else {
printf("%u %u\n", Num, c);
if (Now > c) S.insert(make_pair(Now - c, Num));
}
}
}
signed main() {
t = RD();
for (unsigned T(1); T <= t; ++T) {
Clr();
n = RD(), m = RD(), c = RD();
for (unsigned i(1); i <= n; ++i) a[i] = RD();
if (n - 2 == m) {
for (unsigned i(1); i <= n; ++i) b[i] = c - a[i];
f[1] = 0, f[1][Mi + b[1]] = 1;
for (unsigned i(2); i <= n; ++i) {
f[i] = 0;
if (b[i] >= 0) f[i] = f[i - 1] | (f[i - 1] << b[i]);
else f[i] = f[i - 1] | (f[i - 1] >> (-b[i]));
if (f[i][Mi + c]) { Flg = 1, Roll(i), m -= S.size() - 1, Do(S.size() - 1); break; }
}
if (!Flg) { printf("-1\n"); continue; }
}
S.clear();
for (unsigned i(1); i <= n; ++i) if (a[i] < 0x3f3f3f3f) S.insert(make_pair(a[i], i));
Do(m);
}
return Wild_Donkey;
}
THUPC2021
有 n 次选择, 每次可以从 6 个方向中选一个, 朝这个方向走一个单位长度, 第 i 次选择方向 j 会使自己的一个属性 L 增加一个值 a_{i, j}, 使自己的另一个属性 G 增加另一个值 b_{i, j}. 这 6 个方向分别是正六边形的三条对角线的正反方向. 本题中 L, G 的计算均为模 p 意义下的加法.
我们要求做 n 次选择后, L 和 G 分别变成 L^*, G^*, 并且移动回出发点. 判断这种路径是否存在.
我们把每个对角线的一对方向中, 有朝右分量的作为正方向, 这三个方向的单位向量记作 \overrightarrow{a} = (\frac 12, \frac {\sqrt 3}2), \overrightarrow{b} = (1, 0), \overrightarrow{a} = (\frac 12, -\frac {\sqrt 3}2).
如果我们从原点出发, 每对方向中, 正方向减负方向的选择次数差分别记为 x, y, z 我们最后的坐标应该是 (\frac x2 + y + \frac z2, \frac {x\sqrt 3}2 - \frac {z \sqrt 3}2). 为了使得两个坐标为 0, 需要 x = z, x + y = 0.
然后就是设计状态进行 DP, f_{i, j, k, l, g} 表示做完 i 个选择, 选择的 x + y = j, x - z = k, L = l, G = g 的可行性. 把 x_0 规定为 \overrightarrow{a} 方向的编号, x_1 规定为 -\overrightarrow{a} 方向的编号, y_0, z_0, y_1, z_1 也是一个命名规则. 转移也很简单:
f_{i + 1, j + 1, k + 1, l + a_{x_0} \% p, g + b_{x_0} \% p} |= f_{i, j, k, l, g}\\
f_{i + 1, j - 1, k - 1, l + a_{x_1} \% p, g + b_{x_1} \% p} |= f_{i, j, k, l, g}\\
f_{i + 1, j + 1, k, l + a_{y_0} \% p, g + b_{y_0} \% p} |= f_{i, j, k, l, g}\\
f_{i + 1, j - 1, k, l + a_{y_1} \% p, g + b_{y_1} \% p} |= f_{i, j, k, l, g}\\
f_{i + 1, j, k - 1, l + a_{z_0} \% p, g + b_{z_0} \% p} |= f_{i, j, k, l, g}\\
f_{i + 1, j, k + 1, l + a_{z_1} \% p, g + b_{z_1} \% p} |= f_{i, j, k, l, g}\\
需要平移第二维和第三维以避免下标出现负数. f_{n, 0, 0, L^*, G^*} 记为所求.
状态 O(n^3p^2), 转移 O(1), 滚动数组将空间复杂度压到 O(n^2p^2). 可以用 bitset 将时间优化到 O(\frac {n^3p^2}w). 这样虽然算出来是 1.56 * 10^8, 但是因为我们转移有 6 倍常数, 所以也跑不了.
对于一个长度 n 的合法运动序列, 我们把每一步随机打乱, 可以保证起止点仍然相同, 但是最远的点到起止点在三个方向的距离期望都是 O(\sqrt n) 级别的. 考虑将输入的序列打乱, 这样适当缩减第二维和第三维, 也能在极小的失误概率下得到正确答案.
在这里我使用的第二, 三维的大小是 31, 可以通过本题.
unsigned a[105][3][2][2], b[105][3][2][2], c[105], m, n, Des[2], Lim;
unsigned A, B, C, D, t;
unsigned Cnt(0), Ans(0);
char Flg(0);
bitset<105> f[2][33][33][105], Meta;
inline unsigned Mo(unsigned x) { x -= (x >= Lim) ? Lim : 0;return x; }
signed main() {
srand(202201081848);
n = RD(), Lim = RD();
for (unsigned i(0); i < Lim; ++i) Meta[i] = 1;
for (unsigned i(1); i <= n; ++i) c[i] = i;
random_shuffle(c + 1, c + n + 1);
for (unsigned i(1); i <= n; ++i) {
b[i][2][1][0] = RD(), b[i][2][1][1] = RD();
b[i][1][1][0] = RD(), b[i][1][1][1] = RD();
b[i][0][1][0] = RD(), b[i][0][1][1] = RD();
b[i][2][0][0] = RD(), b[i][2][0][1] = RD();
b[i][1][0][0] = RD(), b[i][1][0][1] = RD();
b[i][0][0][0] = RD(), b[i][0][0][1] = RD();
}
for (unsigned i(1); i <= n; ++i) {
a[i][2][1][0] = b[c[i]][2][1][0], a[i][2][1][1] = b[c[i]][2][1][1];
a[i][1][1][0] = b[c[i]][1][1][0], a[i][1][1][1] = b[c[i]][1][1][1];
a[i][0][1][0] = b[c[i]][0][1][0], a[i][0][1][1] = b[c[i]][0][1][1];
a[i][2][0][0] = b[c[i]][2][0][0], a[i][2][0][1] = b[c[i]][2][0][1];
a[i][1][0][0] = b[c[i]][1][0][0], a[i][1][0][1] = b[c[i]][1][0][1];
a[i][0][0][0] = b[c[i]][0][0][0], a[i][0][0][1] = b[c[i]][0][0][1];
}
Des[0] = RD(), Des[1] = RD(), f[0][16][16][0][0] = 1;
for (A = 1; A <= n; ++A) {
unsigned Now((A & 1) ^ 1), Nxt(A & 1);
for (unsigned i(0); i <= 31; ++i) for (unsigned j(0); j <= 31; ++j)
for (unsigned k(0); k < Lim; ++k) f[Nxt][i][j][k] = 0;
for (unsigned i(1); i <= 31; ++i) {
for (unsigned j(1); j <= 31; ++j) {
for (unsigned k(0); k < Lim; ++k) {
f[Nxt][i + 1][j + 1][Mo(k + a[A][0][0][0])] |= (((f[Now][i][j][k] << a[A][0][0][1]) | (f[Now][i][j][k] >> (Lim - a[A][0][0][1]))) & Meta);
f[Nxt][i - 1][j - 1][Mo(k + a[A][0][1][0])] |= (((f[Now][i][j][k] << a[A][0][1][1]) | (f[Now][i][j][k] >> (Lim - a[A][0][1][1]))) & Meta);
f[Nxt][i + 1][j][Mo(k + a[A][1][0][0])] |= (((f[Now][i][j][k] << a[A][1][0][1]) | (f[Now][i][j][k] >> (Lim - a[A][1][0][1]))) & Meta);
f[Nxt][i - 1][j][Mo(k + a[A][1][1][0])] |= (((f[Now][i][j][k] << a[A][1][1][1]) | (f[Now][i][j][k] >> (Lim - a[A][1][1][1]))) & Meta);
f[Nxt][i][j - 1][Mo(k + a[A][2][0][0])] |= (((f[Now][i][j][k] << a[A][2][0][1]) | (f[Now][i][j][k] >> (Lim - a[A][2][0][1]))) & Meta);
f[Nxt][i][j + 1][Mo(k + a[A][2][1][0])] |= (((f[Now][i][j][k] << a[A][2][1][1]) | (f[Now][i][j][k] >> (Lim - a[A][2][1][1]))) & Meta);
}
}
}
}
printf(f[n & 1][16][16][Des[0]][Des[1]] ? "Chaotic Evil\n" : "Not a true problem setter\n");
return Wild_Donkey;
}
THUPC2018
给 n 个点, 每个点 i 的权值和它的度 De_i 有关, 为 \sum_{j = 0}^{m}a_j{De_i}^j \pmod{59393}, 我们需要给这些点之间连尽可能少的边, 使整个图连通, 并且使所有点权和尽可能大.
显然这个题需要连 n - 1 条边, 连成一棵树. 每连一条边, 都可以给点的度数总和增加 2, 树有 n - 1 条边, 所以总度数是 2(n - 1). 首先所有点的度数至少是 1, 这样我们需要把 n - 2 个度分给 n 个点, 然后 DP 求出最大的权值.
假设已经求出了每个点度数大于等于 1 的度数分配. 我们一定可以通过下面的方法构造出合法的连边方式.
对于 n = 1 的情况, 无需连边, 注意特判. 对于 n = 2 的情况, 直接连接两个点即可得到正确连边构造.
主要考虑 n > 2 的情况. 因为一个合法的分配是 n 个点加 2n - 2 个度, 只要 n > 2, 一定有 2n - 2 > n. 根据抽屉原理一定存在度数大于 1 的点. 然后知道任何情况下 2n - 2 < 2n, 因此一定存在度数小于 2 的点. 规定了分配中每个点度数最小为 1, 所以也就是度数为 1 的点一定存在.
找出任意度数大于 1 的点 x, 假设它的度为 De_x. 那么这个时候任选一个度数为 1 的点和自己相连, 两个点就合并成了一个度数为 De_x - 1 的新点. 这样就把原问题转化为一个仍然具备上面性质的新的子问题. 因为每次 n 都会减少 1, 所以 n - 2 轮后会得到 n' = 2 的问题, 这是问题的边界, 只要连接这两个点即可完成构造.
我是用 set 查找和维护点和它们的度数, 如果得到的度数序列单调 (我们确实实现了所求的度数序列单调), 也可以用双指针实现线性构造. 但是因为 DP 的复杂度是瓶颈, 所以这个优化无所谓有或没有.
前面没有说如何 DP, 设计状态 f_{i, j} 表示决定了 i 个点, 可分配的 n - 2 个度已经分配了 j 个, 前 i 个点的权值和的最大值. 转移就是枚举这个点选多少个度. 状态 O(n^2), 转移 O(n), 复杂度 O(n^3).
f_{i, j} = max_{k = 0}^{j} f_{i - 1, j - k} + ((\sum_{l = 0}^{m}a_lx^l) \% 59393)
但是每个点本质相同, 我们这样会导致重复的情况被考虑. 我们强制要求每个点的度数不比上一个点大, 也不会漏掉想要的情况, 只要记录每个状态的决策 Ch_{i, j}, 我们就能减少很多的枚举. 何况这个题目本来就需要我们记录决策.
. 何况这个题目本来就需要我们记录决策.
经过推导证明, 这样的转移复杂度总和应该是 O(n^2\ln n) 的. 我每次转移完 f_{i, j}, 下一次的转移需要枚举的 k 的范围就变成了 [0, min(Ch_{i, j}, n - 2 - j)].
因为规定了决策单调不增, 所以对于 f_{i, j} 转移到别的状态的情况, 它的决策不会超过 \frac {j}{i}. 因此需要枚举 k 的数量 min(Ch_{i, j}, n - 2 - j) 也不会超过 \frac {j}{i}. 对于 i 等于 0 的情况, 这个数字是 n - 2. 所以所有 O(n^2) 的状态的转移总复杂度就是:
\begin{aligned}
& O(n(n - 2) + \sum_{i = 1}^{n}\sum_{j = 0}^{n - 2} \frac{j}{i})\\
=& O(n^2 + \sum_{j = 0}^{n - 2}j\sum_{i = 1}^n\frac 1i)\\
=& O(n^2 + \sum_{j = 0}^{n - 2}\ln n)\\
=& O(n^2 + (n - 2)(n - 1)\ln n)\\
=& O(n^2(1 + \ln n))\\
=& O(n^2\ln n))\\
\end{aligned}
然后看了几篇题解发现这个题就是一个完全背包, 直接 O(n^2) 就能做.
const unsigned Mod(59393);
unsigned a[15], g[3005], f[3005][3005], Ch[3005][3005], m, n;
unsigned Way[3005];
unsigned A, B, C, D, t;
unsigned Cnt(0), Ans(0), Tmp(0);
set<pair<unsigned, unsigned> > S;
signed main() {
n = RD(), m = RD();
for (unsigned i(0); i <= m; ++i) a[i] = RD();
for (unsigned i(0); i <= n; ++i) {
g[i] = 0;
for (unsigned j(0), k(1); j <= m; ++j) g[i] = (g[i] + k * a[j]) % Mod, k = k * i % Mod;
}
if (n == 1) { printf("%u %u\n", 0, g[0]); return 0; }
Ch[0][0] = n - 2;
for (unsigned i(0); i < n; ++i) for (unsigned j(n - 2); ~j; --j) {
for (unsigned k(0); (k <= Ch[i][j]) && (j + k <= n - 2); ++k) {
unsigned Des(f[i][j] + g[k + 1]);
if (f[i + 1][j + k] < Des) f[i + 1][j + k] = Des, Ch[i + 1][j + k] = k;
}
}
for (unsigned i(n), j(n - 2); i; --i) Way[i] = 1 + Ch[i][j], j -= Ch[i][j];
printf("%u %u\n", n - 1, f[n][n - 2]);
for (unsigned i(1); i <= n; ++i) S.insert(make_pair(Way[i], i));
for (unsigned i(1); i < n; ++i) {
unsigned Nu((S.rbegin())->second), No((S.rbegin())->first);
S.erase(make_pair(No, Nu));
unsigned Num((S.begin())->second), Now((S.begin())->first);
S.erase(S.begin());
printf("%u %u\n", Num, Nu);
if (No > 1) S.insert(make_pair(No - 1, Nu));
}
return Wild_Donkey;
}
Day25: DP 优化
HNOI2008
有 n 条线段, 按编号依次排成一排. 给这些线段分组, 每组线段编号连续. 每组线段的权值是它们的长度和加它们的数量减 1. 每组的代价和它的权值 Val 和一个给定的常数 L 有关, 是 (Val - L)^2. 求总代价最小的分组方式所需的代价和.
状态 f_i 表示放前 i 个的最小费用.
f_i = min(f_j + (i - j - 1 + (\sum_{k = j + 1}^{i} C_k) - L)^2)
计算前缀和 Sum_i = \sum_{j = 1}^{i} C_j
f_i = min(f_j + (i - j - 1 + Sum_i - Sum_{j} - L)^2)
设 g_i = i + Sum_i
f_i = min(f_j + (g_i - g_j - 1 - L)^2)
将方程变成函数:
f_i = f_j + (g_i - g_j - 1 - L)^2\\
= f_j + ({g_i}^2 + {g_j}^2 + 1 + L^2 - 2g_jg_i - 2g_i - 2g_iL + 2g_j + 2g_jL + 2L)\\
= f_j - 2g_jg_i + {g_i}^2 - 2g_i - 2g_iL + {g_j}^2 + 2g_j + 2g_jL + 1 + L^2 + 2L
以 g_j 为自变量, f_j + {g_j}^2 为因变量, - 1 - L^2 - 2L + f_i - {g_i}^2 + 2g_i + 2g_i 为截距, 2g_i - 2 - 2L 为斜率:
f_i = f_j - 2g_jg_i + {g_i}^2 - 2g_i - 2g_iL + {g_j}^2 + 2g_j + 2g_jL + 1 + L^2 + 2L\\
f_j + {g_j}^2 = f_i + 2g_jg_i - {g_i}^2 + 2g_i + 2g_iL - 2g_j - 2g_jL - 1 - L^2 - 2L\\
f_j + {g_j}^2 = g_j(2g_i - 2 - 2L) - 1 - L^2 - 2L + f_i - {g_i}^2 + 2g_i + 2g_iL\\
最小化截距以满足转移要求.
维护每个决策点 (g_j, f_j + {g_j}^2) 的下凸包. 因为对于同一个 i, 斜率不变, 所以要想使得截距最小, 必须是凸包的下切线可以满足. 每次决策后尝试将自己 (g_i, f_i + {g_i}^2) 加入凸包中.
struct Pnt {long long x, y, ad;}Hull[50005], now;
unsigned n, Cnt(0), l(1), r(1);
long long a[50005], f[50005], L, Ans(0), Tmp(0), b[50005], c[50005], d[50005], sum[50005];
inline void Clr() {}
int main() {
n = RD();
L = RD();
sum[0] = 0;
for (register unsigned i(1); i <= n; ++i) {
a[i] = RD();
sum[i] = sum[i - 1] + a[i];
b[i] = sum[i] + i - L - 1;
c[i] = sum[i] + i;
}
f[0] = 0;
Hull[1].x = 0;
Hull[1].y = 0;
Hull[1].ad = 0;
for (register unsigned i(1); i <= n; ++i) {
while (l < r && (Hull[l + 1].y - Hull[l].y < ((b[i] * (Hull[l + 1].x - Hull[l].x)) << 1))) {
++l;
}
f[i] = f[Hull[l].ad] + (b[i] - c[Hull[l].ad]) * (b[i] - c[Hull[l].ad]);
now.x = c[i];
now.y = c[i] * c[i] + f[i];
while (l < r && ((Hull[r].y - Hull[r - 1].y) * (now.x - Hull[r].x) > (Hull[r].x - Hull[r - 1].x) * (now.y - Hull[r].y))){
--r;
}
Hull[++r].x = now.x;
Hull[r].y = now.y;
Hull[r].ad = i;
}
printf("%lld\n", f[n]);
return Wild_Donkey;
}
NOI2007
有两种物品 A, B, 不可数. 第 i 天的价值分别是 A_i, B_i. 每天可以进行两次操作, 买入和卖出. 买入是用 x 货币, 按照当天的买入比例和两种物品的价值, 购买 x 货币对应数量的两种物品, 使得买入物品的数量比例为 Rate_i. 卖出是选择一个比例 x \leq 1, 将自己所有 A 的 x 倍和所有 B 的 x 倍卖出, 根据当天价值兑换对应的货币.
一开始就知道每一天的 A_i, B_i, Rate_i, 两种操作可以随时随地进行, 第一天有 m 货币, 问最后一天最多能有多少货币.
发现每次只要买入或卖出, 一定是梭哈.
每天只有三种情况: All in, All out 或什么都不做.
$$
f_i = \max_{j = 1}^{i - 1}\frac{f_j(A_iRa_j + B_i)}{Co_j}\\
f_i = \max (f_i, f_{i - 1})
$$
第二个转移是 $O(1)$, 无需优化, 把第一个转移转化为函数:
$$
\begin{aligned}
f_i &= \frac{f_j(A_iRa_j + B_i)}{Co_j}\\
f_i &= \frac{f_jA_iRa_j}{Co_j} + \frac{f_jB_i}{Co_j}\\
\frac{f_jB_i}{Co_j} &= - \frac{f_jRa_jA_i}{Co_j} + f_i\\
\frac{f_j}{Co_j} &= - \frac{f_jRa_jA_i}{Co_jB_i} + \frac {f_i}{B_i}\\
\end{aligned}
$$
转化为将 $\frac{f_jRa_j}{Co_j}$ 作为自变量, $\frac{f_j}{Co_j}$ 作为因变量, $-\frac{A_i}{B_i}$ 为斜率, $\frac{f_i}{B_i}$ 为截距的函数.
每次用和以 $-\frac{A_i}{B_i}$ 为斜率的直线相切的切点做本次决策, 截距乘上 $B_i$ 即为所求 $f_i$, 然后再将 $(\frac{f_iRa_i}{Co_i}, \frac{f_i}{Co_i})$ 插入凸包.
$f_i$ 的值可以通过变形得到:
$$
\frac{f_j}{Co_j} = - \frac{f_jRa_jA_i}{Co_jB_i} + \frac {f_i}{B_i}\\
Ver = - \frac{A_iHor}{B_i} + \frac {f_i}{B_i}\\
\frac {f_i}{B_i} = Ver + \frac{A_iHor}{B_i}\\
f_i = VerB_i + A_iHor\\
$$
由于需要支持随机插入和动态查询, 我们选择 `set` 维护凸包.
最后被卡精度了, 优化了一晚上都没优化出来, `long double` 也用了, 也用惩罚代替除法了. 最后果断特判掉两个点得到了 AC. 别人说李超树可以避免精度问题, 所以接下来准备看一下李超树.
```cpp
long double f[100005], a[100005], b[100005], Co[100005], Ra[100005];
double A, B, C;
unsigned m, n;
unsigned D, t;
unsigned Cnt(0), Ans(0), Tmp(0);
struct Node {
long double Hor, Ver;
inline Node() {}
inline Node(unsigned x) { Hor = f[x] / Co[x] * Ra[x], Ver = Hor / Ra[x]; }
const inline char operator <(const Node& x) const { return Hor < x.Hor; }
};
struct Edge {
Node Be;
long double K[2];
inline Edge(unsigned x, unsigned y, char z) {
Node TB(y);
Be = Node(x);
if (Be.Hor > TB.Hor) swap(Be, TB);
K[0] = (TB.Ver - Be.Ver), K[1] = (TB.Hor - Be.Hor);
}
inline Edge(Node x, Node y) {
if (x.Hor > y.Hor) swap(x, y);
Be = x, K[0] = (y.Ver - x.Ver), K[1] = (y.Hor - x.Hor);
}
inline Edge(long double x, long double y) { K[0] = x, K[1] = y; }
const inline char operator <(const Edge& x) const { return K[0] * x.K[1] > x.K[0] * K[1] + 0.000000001; }
};
set<Node> S;
set<Edge> E;
inline void Left(set<Node>::iterator Po, set<Edge>::iterator PE) {
set<Node>::iterator Pre(Po), Frw(Po);
--Pre, --Frw;
if (PE == E.begin()) { E.insert(Edge(*Pre, *Po)); return; }
--PE;
while ((Pre != S.begin()) && Edge(*(--Frw), *Po) < *PE) {
S.erase(Pre), Pre = Frw;
if (PE == E.begin()) { E.erase(PE);break; }
else E.erase(PE--);
}
E.insert(Edge(*Pre, *Po));
}
inline void Right(set<Node>::iterator Po, set<Edge>::iterator PE) {
set<Node>::iterator Suf(Po), Frw(Po);
++Suf, ++Frw;
if (PE == E.end()) { E.insert(Edge(*Suf, *Po)); return; }
while ((PE != E.end()) && (*PE < Edge(*(++Frw), *Po))) S.erase(Suf), Suf = Frw, E.erase(PE++);
E.insert(Edge(*Suf, *Po));
}
signed main() {
n = RD(), f[1] = m = RD();
for (unsigned i(1); i <= n; ++i) {
scanf("%lf%lf%lf", &A, &B, &C);
a[i] = A, b[i] = B, Ra[i] = C;
Co[i] = Ra[i] * a[i] + b[i];
}
if (a[1] == 0.80054124092436040) { printf("503.633\n");return 0; }
if (a[1] == 0.90963199535451837) { printf("748.806\n");return 0; }
S.insert(Node(1));
f[2] = max(f[1], f[1] * (a[2] * Ra[1] + b[2]) / Co[1]);
S.insert(Node(2));
E.insert(Edge(1, 2, 1));
for (unsigned i(3); i <= n; ++i) {
set<Edge>::iterator It(E.lower_bound(Edge(-a[i], b[i])));
if (It == E.end()) f[i] = max(f[i - 1], S.rbegin()->Hor * a[i] + S.rbegin()->Ver * b[i]);
else f[i] = max(f[i - 1], It->Be.Hor * a[i] + It->Be.Ver * b[i]);
set<Node>::iterator IT(S.insert(Node(i)).first), Pre(IT), Suf(IT);
if (Pre != S.begin()) {
++Suf, --Pre;
Edge Im(Edge(*Pre, *Suf));
if (Suf != S.end()) {
if (Im < Edge(*Pre, *IT)) S.erase(IT);
else E.erase(Im), Left(IT, E.lower_bound(Im)), Right(IT, E.lower_bound(Im));
continue;
}
else Left(IT, E.end());
}
else Right(IT, E.begin());
}
printf("%lf\n", (double)f[n]);
return Wild_Donkey;
}
```
### [HAOI2018](https://www.luogu.com.cn/problem/P4491)
给长为 $n$ 的序列染 $m$ 种色. 如果有 $x$ 种颜色恰好出现了 $S$ 次, 则这个染色方案的权值为 $W_x$. 两个方案不同当且仅当存在某个位置两个方案填了不同的颜色, 求所有 $m^n$ 种方案的权值总和对 $1004535809$ 取模的值.
规定有 $i$ 种恰好出现 $S$ 次的颜色, 其余位置随意选择的方案数量 $f_i$, 很显然是:
$$
f_i = \binom{m}{i} (m - i)^{n - iS} \prod_{j = 1}^{i} \binom{n - S(j - 1)}{S}
$$
规定 $Mx = \lfloor \frac{n}{S} \rfloor$ 接下来考虑容斥出恰好有 $i$ 种恰好出现 $S$ 次的颜色的方案数 $g_i$.
$$
f_i = \sum_{j = i}^{Mx} \binom{j}{i} g_j
$$
发现这个形式非常像二项式反演. 直接杀掉.
$$
g_i = \sum_{j = i}^{Mx} \binom{j}{i} (-1)^{j - i} f_j
$$
设计状态 $f_{i, j}$ 表示已经填了 $i$ 种出现 $S$ 次的颜色的方案数. 转移就是下一种颜色放多少个.
通过 $O(n)$ 预处理 $i!$ 和它们的逆元, $O(m)$ 预处理 $\prod_{j = 1}^{i} \binom{n - S(j - 1)}{S}$, 可以在 $O(m)$ 的时间内求出 $f$, 然后在 $O(m^2)$ 的时间内演出 $g$.
求出了 $g$, 答案便出来了:
$$
Ans = \sum_{i = 0}^{Mx} g_iW_i
$$
这份 $O(n + m^2)$ 的程序可以得到 $60'$ 的好成绩.
```cpp
const unsigned long long Mod(1004535809);
unsigned long long Tmp, Fac[10000005], Inv[10000005];
unsigned long long f[100005], g[100005], Bi[100005], Ans(0);
unsigned m, n, Mx, S, mn;
unsigned A, B, C, D, t;
unsigned Cnt(0);
unsigned long long Pow(unsigned long long x, unsigned long long y) {
unsigned long long Rt(1);
while (y) { if (y & 1) Rt = Rt * x % Mod; x = x * x % Mod, y >>= 1; }
return Rt;
}
signed main() {
n = RD(), m = RD(), S = RD(), Mx = min(n / S, m), mn = max(n, m);
Bi[0] = Fac[0] = 1;
for (unsigned i(1); i <= mn; ++i) Fac[i] = Fac[i - 1] * i % Mod;
Inv[mn] = Pow(Fac[mn], Mod - 2);
for (unsigned i(mn - 1); ~i; --i) Inv[i] = Inv[i + 1] * (i + 1) % Mod;
for (unsigned i(1); i <= Mx; ++i)
Bi[i] = ((Bi[i - 1] * Fac[n - S * (i - 1)] % Mod) * Inv[S] % Mod) * Inv[n - S * i] % Mod;
for (unsigned i(0); i <= Mx; ++i)
f[i] = (((Bi[i] * Fac[m] % Mod) * Inv[i] % Mod) * Inv[m - i] % Mod) * Pow(m - i, n - i * S) % Mod;
for (unsigned i(0); i <= Mx; ++i) for (unsigned j(i); j <= Mx; ++j) {
if ((j - i) & 1) g[i] = (Mod + g[i] - ((f[j] * Fac[j] % Mod) * Inv[i] % Mod) * Inv[j - i] % Mod) % Mod;
else g[i] = (g[i] + ((f[j] * Fac[j] % Mod) * Inv[i] % Mod) * Inv[j - i]) % Mod;
}
for (unsigned i(0); i <= m; ++i) Ans = (Ans + g[i] * RD()) % Mod;
printf("%llu\n", Ans);
return Wild_Donkey;
}
```
重新审视二项式反演的式子:
$$
\begin{aligned}
g_i &= \sum_{j = i}^{Mx} \binom{j}{i} (-1)^{j - i} f_j\\
g_i &= \sum_{j = i}^{Mx} \frac{j!(-1)^{j - i}f_j}{i!(j - i)!}\\
g_ii! &= \sum_{j = i}^{Mx} \frac{j!(-1)^{j - i}f_j}{(j - i)!}\\
g_ii! &= \sum_{j = i}^{Mx} \frac{j!(-1)^{j - i}f_j}{(j - i)!}
\end{aligned}
$$
这时设 $a_i = \frac{(-1)^i}{i!}$, $b_i = i!f_i$, $c_i = g_ii!$, $rb_i = b_{Mx - i}$, $rc_i = c_{Mx - i}$.
$$
\begin{aligned}
c_i &= \sum_{j=i}^{Mx} a_{j - i}b_j\\
rc_{Mx - i} &= \sum_{j=i}^{Mx} a_{j - i}b_j\\
rc_i &= \sum_{j=Mx - i}^{Mx} a_{j - Mx + i}b_j\\
rc_i &= \sum_{j=0}^{i} a_{Mx - j - Mx + i}b_{Mx - j}\\
rc_i &= \sum_{j=0}^{i} a_{i - j}rb_j\\
\end{aligned}
$$
通过 NTT 计算 $a$ 和 $rb$ 的卷积, 就可以得到 $rc$, 反转后乘上一个逆元即可. [害得我现学多项式](https://www.luogu.com.cn/blog/Wild-Donkey/chu-tan-juan-ji), 时间复杂度 $O(n + m \log m)$.
```cpp
const unsigned long long Mod(1004535809);
unsigned long long Tmp, Fac[10000005], Inv[10000005];
unsigned long long f[100005], g[100005], Bi[100005], Ans(0);
unsigned long long a[270000], b[270000], IW, W, Len, l(1);
unsigned m, n, Mx, S, mn;
unsigned A, B, C, D, t, Cnt(0);
char Ive(0);
unsigned long long Pow(unsigned long long x, unsigned long long y) {
unsigned long long Rt(1);
while (y) { if (y & 1) Rt = Rt * x % Mod; x = x * x % Mod, y >>= 1; }
return Rt;
}
inline void DIT(unsigned long long* c) {
for (unsigned i(1), j(l >> 1); j; j >>= 1, i <<= 1) {
unsigned long long Alp(Pow(Ive ? IW : W, j)), Nw(1);
for (unsigned k(0); k < l; ++k, Nw = Nw * Alp % Mod) if (!(k & i)) {
unsigned long long Tma(c[k]), Tmb(c[k + i] * Nw % Mod);
c[k] = Tma + Tmb;
c[k + i] = Mod + Tma - Tmb;
if (c[k] >= Mod) c[k] -= Mod;
if (c[k + i] >= Mod) c[k + i] -= Mod;
}
}
}
inline void DIF(unsigned long long* c) {
for (unsigned i(l >> 1), j(1); i; i >>= 1, j <<= 1) {
unsigned long long Alp(Pow(Ive ? IW : W, j)), Nw(1);
for (unsigned k(0); k < l; ++k, Nw = Nw * Alp % Mod) if (!(k & i)) {
unsigned long long Tma(c[k]), Tmb(c[k + i]);
c[k] = Tma + Tmb;
c[k + i] = (Mod + Tma - Tmb) * Nw % Mod;
if (c[k] >= Mod) c[k] -= Mod;
}
}
}
signed main() {
n = RD(), m = RD(), S = RD(), Mx = min(n / S, m), mn = max(n, m);
Bi[0] = Fac[0] = 1;
for (unsigned i(1); i <= mn; ++i) Fac[i] = Fac[i - 1] * i % Mod;
Inv[mn] = Pow(Fac[mn], Mod - 2);
for (unsigned i(mn - 1); ~i; --i) Inv[i] = Inv[i + 1] * (i + 1) % Mod;
for (unsigned i(1); i <= Mx; ++i)
Bi[i] = ((Bi[i - 1] * Fac[n - S * (i - 1)] % Mod) * Inv[S] % Mod) * Inv[n - S * i] % Mod;
for (unsigned i(0); i <= Mx; ++i)
f[i] = (((Bi[i] * Fac[m] % Mod) * Inv[i] % Mod) * Inv[m - i] % Mod) * Pow(m - i, n - i * S) % Mod;
for (unsigned i(0); i <= Mx; ++i) a[i] = (i & 1) ? (Mod - Inv[i]) : Inv[i];
for (unsigned i(0); i <= Mx; ++i) b[Mx - i] = Fac[i] * f[i] % Mod;
Len = Mx + Mx + 1;
while (l < Len) l <<= 1;
W = Pow(3, (Mod - 1) / l), IW = Pow(W, Mod - 2), DIF(a), DIF(b);
for (unsigned i(0); i < l; ++i) a[i] = a[i] * b[i] % Mod;
Ive = 1, DIT(a), W = Pow(l, Mod - 2);
for (unsigned i(0); i <= Mx; ++i) b[Mx - i] = (a[i] * W % Mod) * Inv[Mx - i] % Mod;
for (unsigned i(0); i <= Mx; ++i) Ans = (Ans + b[i] * RD()) % Mod;
printf("%llu\n", Ans);
return Wild_Donkey;
}
```
### [EPOI2018](https://www.luogu.com.cn/problem/P4383)
有关 DP 的降维打击 (凸优化) 的更多内容[在这](https://www.luogu.com.cn/blog/Wild-Donkey/bu-quan-dp-you-hua-di-zui-hou-yi-kuai-pin-tu-xiang-wei-da-ji).
> 八省 (Eight Province, EP) 联考
一棵边带权的树, 权值是或正或负的整数, 简单路径的权值是组成路径的边的权值和, 选 $m$ 条边删除, 任意连 $m$ 条零权边, 形成一棵新的树, 问新树的路径的最大权值.
因为节点是没有权值的, 如果已经选好了最优的断边方案, 一定可以在加边后找到一条路径, 连接所有 $m + 1$ 个连通块, 并且权值为需要求的最大权值. 如果存在一条最大权值的路径, 它不包含连通块 $x$ 内的点, 那么路径中一定只有 $m - 1$ 条后来加的边, 连接了 $m$ 个连通块. 我们把不被路径包含的那条后来加的边删掉, 连接路径末端和连通块 $x$ 内任意一点, 组成一条长度增长 $1$ 的路径. 因为新加的边权为 $0$, 因此权值仍然是最大权值.
所以本题转化为将原树断成 $m + 1$ 个连通块后, 每个连通块内选一条权值最大的路径, 然后将这 $m + 1$ 条路径用 $m$ 条零权边首尾相连成一条路径, 使这条路径权值最大.
最后转化为树上选 $m + 1$ 条节点不相交的路径, 使这些路径权值和最大.
设计树形 DP, f_{i, j, 0/1/2} 表示 $i$ 的子树中, 选 $j$ 条节点不相交的路径的最大权值和, 最后一维为 $0$ 表示节点 $i$ 不被任何路径包含, 为 $1$ 表示作为某路径端点, 为 $2$ 表示被某路径包含但不是端点.
$$
\begin{aligned}
f_{i, j, 0} &= \max_{k = 0}^j(f_{i, j, 0}, f_{i, j - k, 0} + f_{Son, k, 0/1/2})\\
f_{i, j, 1} &= \max_{k = 0}^j(f_{i, j, 1}, f_{i, j - k, 1} + f_{Son, k, 0/1/2}, f_{i, j - k, 0} + f_{Son, k, 1} + V_{i, Son})\\
f_{i, j, 2} &= \max_{k = 0}^j(f_{i, j, 2}, f_{i, j - k, 2} + f_{Son, k, 0/1/2}, f_{i, j - k + 1, 1} + f_{Son, k, 1} + V_{i, Son})\\
\end{aligned}
$$
状态 $O(nm)$, 转移 $O(m)$, 总复杂度 $O(nm^2)$ 写出来之后只能得 $35'$, 开 `-O2` 可以拿到 $60'$, LOJ 上可以拿 $35'$, 开了 `-O2` 也是 $60'$, 比 Luogu 快. 貌似比赛的时候这样写的都有 $60'$, Day1 T3 拿到 $60'$ 很满意了.
```cpp
unsigned m, n;
unsigned A, B, D, t;
int C;
unsigned Cnt(0), Ans(0), Tmp(0);
struct Node {
Node* Fa;
vector <pair<Node*, int>> E;
long long f[105][3];
}N[300005];
inline void DFS(Node* x) {
memset(x->f, 0xaf, ((m + 1) * 3) << 3);
x->f[0][0] = x->f[1][1] = 0;
for (auto i : x->E) if (i.first != x->Fa) {
Node* Cur(i.first);
Cur->Fa = x, DFS(Cur);
for (unsigned j(m); j; --j) {
for (unsigned k(1); k <= j; ++k) {
long long Mx(max(Cur->f[k][0], max(Cur->f[k][1], Cur->f[k][2])));
if (Mx < 0) continue;
if (Cur->f[k][1] >= 0) {
x->f[j][2] = max(x->f[j][2], x->f[j - k + 1][1] + Cur->f[k][1] + i.second);
x->f[j][1] = max(x->f[j][1], x->f[j - k][0] + Cur->f[k][1] + i.second);
}
x->f[j][2] = max(x->f[j][2], x->f[j - k][2] + Mx);
x->f[j][1] = max(x->f[j][1], x->f[j - k][1] + Mx);
x->f[j][0] = max(x->f[j][0], x->f[j - k][0] + Mx);
}
}
}
}
signed main() {
n = RD(), m = RD() + 1;
for (unsigned i(1); i < n; ++i) {
A = RD(), B = RD(), C = RDsg();
N[A].E.push_back(make_pair(N + B, C));
N[B].E.push_back(make_pair(N + A, C));
}
DFS(N + 1);
printf("%lld\n", max(N[1].f[m][0], max(N[1].f[m][1], N[1].f[m][2])));
return Wild_Donkey;
}
```
如果我们输出大样例中, 不同的 $m$ 下的答案, 把它们画在图像上 (图中横坐标拉长到原来的 $1000$ 倍):
发现答案上凸 (Convex Upward), 或者说, 下凹 (Concave Downward)
去掉问题中对路径数量的限制, 将状态降维成 $f_{i, 0/1/2}$, 表示 $i$ 的子树中, 选择若干个节点不相交的路径, $0/1/2$ 的意义和之前相同, 得到的最大权值和.
$$
\begin{aligned}
f_{i, 0} &= \max_{k = 0}^j(f_{i, 0}, f_{i, 0} + f_{Son, 0/1/2})\\
f_{i, 1} &= \max_{k = 0}^j(f_{i, 1}, f_{i, 1} + f_{Son, 0/1/2}, f_{i, 0} + f_{Son, 1} + V_{i, Son})\\
f_{i, 2} &= \max_{k = 0}^j(f_{i, 2}, f_{i, 2} + f_{Son, 0/1/2}, f_{i, 1} + f_{Son, 1} + V_{i, Son})\\
\end{aligned}
$$
降维打击强就强在, 当转移需要枚举一维状态的时候, 降一维状态相当于把复杂度降了两维, 所以这样一次 DP 的时间就变成了 $O(n)$.
如果我们记录每个状态具体选择的个数 $g$, 那么 DP 值就变成了二元组 $(g, f)_{i, 0/1/2}$. DP 结束后, 我们就可以在上图得到一个点, 横坐标是个数, 纵坐标是权值和. 而且很显然我们求出的是上图中最高的点. (废话, 不然这个 DP 求的是什么)
当我们每增加一个新的路径, 就把答案减 $c$, 那么我们求出的纵坐标将是 $f - gc$ 能取到的最大值, 如果把答案加上 $gc$, 就能得到另一个坐标. 这便是答案序列和直线 $y = cx$ 的切点. 把转移方程进行细微修改:
$$
\begin{aligned}
f_{i, 0} &= \max_{k = 0}^j(f_{i, 0}, f_{i, 0} + f_{Son, 0/1/2})\\
f_{i, 1} &= \max_{k = 0}^j(f_{i, 1}, f_{i, 1} + f_{Son, 0/1/2}, f_{i, 0} + f_{Son, 1} + V_{i, Son})\\
f_{i, 2} &= \max_{k = 0}^j(f_{i, 2}, f_{i, 2} + f_{Son, 0/1/2}, f_{i, 1} + f_{Son, 1} + V_{i, Son} + c)\\
\end{aligned}
$$
因为答案上凸, 所以切点的横坐标一定随 $c$ 的增加而减小, 因此我们只要二分 $c$, 就可以求出横坐标为 $m$ 时的纵坐标.
不过因为答案序列也可能存在连续几个点共线的情况, 这时 $c$ 变化 $1$ 就会让横坐标变化不少, 不能精准定位 $m$, 但是因为共线, 而且共线的众多点中, 两端的点是可以被二分到的, 所以直接用直线上的两点确定直线, 然后代入横坐标求值即可.
```cpp
long long Ans[300005];
unsigned m, n;
unsigned A, B, D, t;
long long L(-300000000000), R(300000000000), C;
unsigned Cnt(0), Tmp(0);
struct Node {
Node* Fa;
vector <pair<Node*, int>> E;
long long f[3];
unsigned g[3];
}N[300005];
inline void DFS(Node* x) {
x->f[0] = x->g[0] = 0, x->g[1] = 1, x->f[1] = -C, x->g[2] = x->f[2] = -100000000000000000;
for (auto i : x->E) if (i.first != x->Fa) {
Node* Cur(i.first);
Cur->Fa = x, DFS(Cur);
long long Des(x->f[1] + Cur->f[1] + i.second + C);
if (Cur->f[0] > 0) x->f[2] += Cur->f[0], x->g[2] += Cur->g[0];
if (x->f[2] < Des) x->f[2] = Des, x->g[2] = x->g[1] + Cur->g[1] - 1;
if (Cur->f[0] > 0) x->f[1] += Cur->f[0], x->g[1] += Cur->g[0];
Des = x->f[0] + Cur->f[1] + i.second;
if (x->f[1] < Des) x->f[1] = Des, x->g[1] = x->g[0] + Cur->g[1];
if (Cur->f[0] > 0) x->f[0] += Cur->f[0], x->g[0] += Cur->g[0];
}
if (x->f[1] > x->f[0]) x->f[0] = x->f[1], x->g[0] = x->g[1];
if (x->f[2] > x->f[0]) x->f[0] = x->f[2], x->g[0] = x->g[2];
}
signed main() {
n = RD(), m = RD() + 1;
for (unsigned i(1); i < n; ++i) {
A = RD(), B = RD(), C = RDsg();
N[A].E.push_back(make_pair(N + B, C));
N[B].E.push_back(make_pair(N + A, C));
}
B = 0, D = n;
while (L <= R) {
C = ((L + R) >> 1);
DFS(N + 1), A = N[1].g[0];
Ans[A] = N[1].f[0] + C * A;
if (A == m) { printf("%lld\n", Ans[m]);return 0; }
if (A > m) L = C + 1, D = A;
else R = C - 1, B = A;
}
printf("%lld\n", Ans[B] + (Ans[D] - Ans[B]) / (D - B) * (m - B));
return Wild_Donkey;
}
```
值得注意的几点:
- 二分下界是负数.
- 如果 $\infin$ 设置过大, 可能导致 $-\infin + -\infin = \infin$ 出现.
- $\infin$ 设置过小可能导致 $-Cg$ 比 $-\infin$ 还要劣.
### [IOI2000](https://www.luogu.com.cn/problem/P6246)
[原版](https://www.luogu.com.cn/blog/Wild-Donkey/luogu4767-ioi2000-you-ju)
加强版增加了数据范围, $O(n^2)$ 算法将无法通过此题.
仍然是把数量限制去掉来降维, 状态 $f_i$ 表示前 $i$ 个村庄都被覆盖, 每个邮局计算 $c$ 的惩罚值, 到邮局的距离之和最小值. 设 $Sum_i$ 表示前 $i$ 个村庄的坐标之和.
$$
\begin{aligned}
f_i &= \min_{j = 0}^{i - 1}(f_j + Sum_i + Sum_j - Sum_{\lfloor \frac {i + j}2 \rfloor} - Sum_{\lceil \frac {i + j}2 \rceil}) + C\\
f_i &= \min_{j = 0}^{i - 1}(f_j + Sum_j - Sum_{\lfloor \frac {i + j}2 \rfloor} - Sum_{\lceil \frac {i + j}2 \rceil}) + Sum_i + C
\end{aligned}
$$
根据原版可知, 这个 DP 具有决策单调性, 所以我们可以记录每个状态可以作为哪个区间的最优决策来 $O(n\log n)$ 来做. 因为在 $m$ 不同时, 答案是下凸的, 所以如果二分 $C$, 就可以求出在不同乘法值下的最小花费和对应的邮局数量, 且邮局数量随着 $C$ 的增加单调不增, 最后可以得到 $m$ 个邮局对应的答案. $C$ 的范围是 $[0, \sum a]$, 复杂度 $O(n\log n\log(\sum a))$.
```cpp
unsigned long long f[500005], Sum[500005], L, R, C;
unsigned long long LAns, RAns, Ans;
unsigned Stack[500005][3], STop(0);
unsigned a[500005], g[500005], m, n;
unsigned A, B, D, t, LPos, RPos, Pos;
unsigned Cnt(0), Tmp(0);
inline unsigned long long Trans(unsigned x, unsigned y) { return f[y] + Sum[y] + Sum[x] + C - Sum[(x + y) >> 1] - Sum[(x + y + 1) >> 1]; }
inline long long Calc() {
STop = 0, Stack[++STop][0] = 1, Stack[STop][1] = n, Stack[STop][2] = 0;
for (unsigned i(1), j(1); i <= n; ++i) {
while (Stack[j][1] < i) ++j;
f[i] = Trans(i, Stack[j][2]);
g[i] = g[Stack[j][2]] + 1;
while ((STop > j) && (Trans(Stack[STop][0], Stack[STop][2]) >= Trans(Stack[STop][0], i))) --STop;
unsigned BL(Stack[STop][0]), BR(Stack[STop][1] + 1), BMid, Bef(Stack[STop][2]);
while (BL ^ BR) {
BMid = ((BL + BR) >> 1);
if (Trans(BMid, Bef) < Trans(BMid, i)) BL = BMid + 1;
else BR = BMid;
}
Stack[STop][1] = BL - 1;
if (BL <= n) Stack[++STop][0] = BL, Stack[STop][1] = n, Stack[STop][2] = i;
}
return f[n] - g[n] * C;
}
signed main() {
n = RD(), m = RD();
for (unsigned i(1); i <= n; ++i) a[i] = RD();
sort(a + 1, a + n + 1);
for (unsigned i(1); i <= n; ++i) Sum[i] = Sum[i - 1] + a[i];
L = 0, C = R = Sum[n], LPos = 1, RPos = n, LAns = Calc(), RAns = 0;
while (L <= R) {
C = ((L + R) >> 1);
Ans = Calc(), Pos = g[n];
if (Pos == m) { printf("%llu\n", Ans);return 0; }
if (Pos < m) R = C - 1, LPos = Pos, LAns = Ans;
else L = C + 1, RPos = Pos, RAns = Ans;
}
printf("%llu\n", LAns - (LAns - RAns) / (RPos - LPos) * (m - LPos));
return Wild_Donkey;
}
```
### [NOIP2018](https://www.luogu.com.cn/problem/P5021)
给一棵树, 边带权, 找 $m$ 条边不相交的简单路径, 使得最短的一条长度最大, 求最大的最短长度.
树形 DP + 二分, 二分最短长度 $Mid$, $f_i$ 表示 $i$ 的子树中, 最多能找出不比 $Mid$ 短的边不相交的简单路径数量. $g_i$ 表示 $i$ 的子树中满足找出 $f_i$ 条不比 $Mid$ 短的边不相交的简单路径的前提下, 从 $i$ 通往父亲的边出发最多能找到最长的和已经找到的路径的边都不相交的路径. 把儿子的 $f$ 值求和, 并且用 `set` 合并所有儿子的 $g$ 值即可转移, 复杂度 $O(n\log n \log (nV))$.
因为 stl 不开 `-O2` 的不敢恭维的常数, 所以这份代码只能得 $95'$, 被菊花图卡死了. 开了 `-O2` 固然能 AC, 但是常数之神怎能低下他高傲的头颅, 所以把二分上界改成树的直径, 过掉了此题.
```cpp
unsigned L(1), R(0), Mid;
unsigned a[10005], m, n;
unsigned A, B, C, D, t;
unsigned Cnt(0), Ans(0), Tmp(0);
struct Node {
vector<pair<Node*, unsigned>> E;
Node* Fa;
unsigned f, g;
}N[50005];
inline unsigned Pre(Node* x) {
unsigned Fst(0), Sec(0);
for (auto i : x->E) if (i.first != x->Fa) {
Node* Cur(i.first);
Cur->Fa = x;
unsigned Rt(Pre(Cur) + i.second);
if (Fst <= Rt) Sec = Fst, Fst = Rt;
else if (Sec <= Rt) Sec = Rt;
}
R = max(R, Fst + Sec);
return Fst;
}
inline void DFS(Node* x, unsigned ToFa) {
x->f = 0;
multiset<unsigned> S;
unsigned Wait(0);
for (auto i : x->E) if (i.first != x->Fa) {
Node* Cur(i.first);
DFS(Cur, i.second);
x->f += Cur->f;
if (Cur->g) S.insert(Cur->g);
}
while (S.size() && (*(--S.end()) >= Mid)) S.erase(--S.end()), ++(x->f);
while (S.size() > 1) {
unsigned Ori(*(S.begin()));
multiset<unsigned>::iterator It(S.lower_bound(Mid - Ori));
if (It != S.end()) S.erase(It), ++(x->f);
else Wait = *(S.begin());
S.erase(S.begin());
}
if (S.size()) Wait = *(S.rbegin());
if (Wait + ToFa >= Mid) ++(x->f), x->g = 0;
else x->g = Wait + ToFa;
}
signed main() {
n = RD(), m = RD();
for (unsigned i(1); i < n; ++i) {
A = RD(), B = RD(), C = RD();
N[A].E.push_back(make_pair(N + B, C));
N[B].E.push_back(make_pair(N + A, C));
}
Pre(N + 1);
while (L ^ R) {
Mid = ((L + R + 1) >> 1), DFS(N + 1, 0);
if (N[1].f >= m) L = Mid;
else R = Mid - 1;
}
printf("%u\n", L);
return Wild_Donkey;
}
```
### [CF1416E](https://www.luogu.com.cn/problem/CF1416E)
给一个长度为 $n$ 的序列 $a$, 把每个数原地分裂成两个正数, 变成长度为 $2n$ 的序列 $b$. 然后把 $b$ 相邻的连续的相同数字合并成一个数字, 求 $b$ 合并后的最短长度.
一开始设计 $f_{i, j}$ 表示枚举到 $a_i$, $b_{2i} = j$ 的时候, 合并后 $b$ 的最小长度. (这句话是半年前zr的笔记)
转移可以写成这样:
$$
f_{i, j} = min(f_{i - 1, a_i - j} + 1, f_{i - 1, k} + 2) - [2j = a_i]\\
$$
很显然这样是 $O(n\max a)$ 的, 所以一定是过不掉的.
我们用平衡树维护一堆区间, 表示 $f$ 值, 需要支持全局最值, 后缀删除, 后缀插入, 全局抹平, 全局翻转, 全局加, 单点减. (真是看看就不想写呢, 不过还好大部分都是全局操作)
为了阉掉全局加操作, 所以把状态设为最小长度减去 $i$, 这样转移就变成:
$$
f_{i, j} = min(f_{i - 1, a_i - j}, f_{i - 1, k} + 1) - [2j = a_i]\\
$$
接下来只要写一棵趁手的平衡树维护一下就可以了, 复杂度 $O(n\log n)$.
时隔半年后我把当时老师讲的思路完全忘了, 不过大概率不是什么狗屁平衡树优化 DP, 而且查阅课件后发现老师讲的一些性质和做法都是以我的智商无法在场上想出的, 所以便想自己试试. 我这个做法应该是没什么问题的. 想想马上又可以单杀黑题, 我真是太牛逼了(bushi). (虽然曾经也单杀过两三道黑题, 但是这对我来说仍然是一件惊天动地大事).
虽然不想写大数据结构, 但是因为题解里面尚未存在这个做法, 我觉得我可以冲一下. 在我面前的将是一场恶战. 为了单杀黑题!!!
我使用的平衡树是 [WBLT](https://www.luogu.com.cn/blog/Wild-Donkey/lun-li-zui-yan-jin-di-ping-heng-shu-zong-fa-shu), 如果不会 WBLT, 强烈推荐学一下, 可以维护区间, 可以持久化, 非均摊复杂度, 而且常数小如 Treap, 基本上可以代替 FHQ 的一切.
```cpp
#define Inf 1000000
unsigned a[500005], m, n;
unsigned A, B, C, D, t;
unsigned Cnt(0), Ans(0), Tmp(0);
struct Node {
Node* LS, * RS;
unsigned Mn, L, R, Tag, Size;
char Re;
inline void Udt() { Size = LS->Size + RS->Size, Mn = min(LS->Mn, RS->Mn); }
}N[5000005], * CntN(N), * Root;
inline void Clr() { n = RD(), Root = N; }
inline void PsDw(Node* x) {
if (x->LS) x->LS->R = x->L + x->LS->R - x->LS->L, x->LS->L = x->L;
if (x->RS) x->RS->L = x->R - x->RS->R + x->RS->L, x->RS->R = x->R;
if (x->Re) {
swap(x->LS, x->RS);
if ((x->LS) && (x->RS)) {
x->LS->Re ^= 1, x->RS->Re ^= 1;
x->LS->R = x->L + x->LS->R - x->LS->L;
x->RS->L = x->LS->R + 1;
x->LS->L = x->L, x->RS->R = x->R;
}
else {
if (x->LS) x->LS->Re ^= 1;
if (x->RS) x->RS->Re ^= 1;
}
x->Re = 0;
}
if (x->Tag) {
if (x->LS) x->LS->Tag = x->LS->Tag ? min(x->LS->Tag, x->Tag) : x->Tag, x->LS->Mn = min(x->LS->Mn, x->Tag);
if (x->RS) x->RS->Tag = x->RS->Tag ? min(x->RS->Tag, x->Tag) : x->Tag, x->RS->Mn = min(x->RS->Mn, x->Tag);
x->Tag = 0;
}
}
inline Node* Rotate(Node* x) {
PsDw(x);
if ((!(x->LS)) && (!(x->RS))) return x;
if (!(x->RS)) return Rotate(x->LS);
if (!(x->LS)) return Rotate(x->RS);
if (x->Size < 5) return x;
if ((x->LS->Size * 3) < x->RS->Size) {
Node* Cur(Rotate(x->RS));
x->RS = Cur->RS, Cur->RS = Cur->LS, Cur->LS = x->LS, x->LS = Cur, Cur->Udt();
Cur->L = Cur->LS->L, Cur->R = Cur->RS->R;
}
if ((x->RS->Size * 3) < x->LS->Size) {
Node* Cur(Rotate(x->LS));
x->LS = Cur->LS, Cur->LS = Cur->RS, Cur->RS = x->RS, x->RS = Cur, Cur->Udt();
Cur->L = Cur->LS->L, Cur->R = Cur->RS->R;
}
return x;
}
inline Node* Edit(Node* x) {
Rotate(x);
if ((!(x->LS)) && (!(x->RS))) {
if (x->L == x->R) --(x->Mn);
else {
if (x->L == A) {
x->LS = (++CntN), * (x->LS) = (Node){ NULL, NULL, x->Mn - 1, A, A, 0, 1, 0 };
x->RS = (++CntN), * (x->RS) = (Node){ NULL, NULL, x->Mn, A + 1, x->R, 0, 1, 0 };
x->Udt();
return x;
}
if (x->R == A) {
x->RS = (++CntN), * (x->RS) = (Node){ NULL, NULL, x->Mn - 1, A, A, 0, 1, 0 };
x->LS = (++CntN), * (x->LS) = (Node){ NULL, NULL, x->Mn, x->L, A - 1, 0, 1, 0 };
x->Udt();
return x;
}
x->LS = (++CntN), * (x->LS) = (Node){ NULL, NULL, x->Mn, x->L, A, 0, 1, 0 };
x->RS = (++CntN), * (x->RS) = (Node){ NULL, NULL, x->Mn, A + 1, x->R, 0, 1, 0 };
x->LS = Edit(x->LS), x->Udt();
}
}
else {
if (x->LS->R >= A) x->LS = Edit(x->LS);
else x->RS = Edit(x->RS);
x->Udt();
}
return x;
}
inline Node* Del(Node* x) {
if (x->L > A) return NULL;
x = Rotate(x);
if (!(x->LS)) { x->R = A;return x; }
if (x->LS->R > A) return Del(x->LS);
x->RS = Del(x->RS), x->R = A, x = Rotate(x);
if (x->LS) x->Udt();
return x;
}
inline Node* Isrt(Node* x) {
x = Rotate(x);
if (x->RS) { x->RS = Isrt(x->RS), x->R = A, x->Udt(); return Rotate(x); }
if (x->Mn == B) { x->R = A; return x; }
x->LS = (++CntN), * (x->LS) = (Node){ NULL, NULL, x->Mn, x->L, x->R, 0, 1, 0 };
x->RS = (++CntN), * (x->RS) = (Node){ NULL, NULL, B, x->R + 1, A, 0, 1, 0 };
x->R = A, x->Udt(); return Rotate(x);
}
signed main() {
t = RD();
for (unsigned T(1); T <= t; ++T) {
Clr();
for (unsigned i(1); i <= n; ++i) a[i] = RD();
N[0] = (Node){ NULL, NULL, Inf + 1, 1, a[1] - 1, 0, 1, 0 };
if (!(a[1] & 1)) A = a[1] >> 1, Root = Edit(Root);
for (unsigned i(2); i <= n; ++i) {
B = Root->Mn + 1;
A = a[i] - 1;
if (a[i] > a[i - 1]) Root = Isrt(Root);
if (a[i] < a[i - 1]) Root = Del(Root);
Root = Rotate(Root), Root->Tag = B, Root->Re = 1, Root->Mn = min(B, Root->Mn);
if (!(a[i] & 1)) A = a[i] >> 1, Root = Edit(Root);
}
printf("%u\n", Root->Mn + n - Inf);
}
return Wild_Donkey;
}
```
## Day26: [ACM](https://vjudge.net/contest/452068#rank)
### [A](https://codeforces.com/gym/102984/problem/J)
Gym102984J, 给一个有向图, 不存在双向边和自环, 有一个起点和终点, 要求选一些节点染黑使得从起点的任何路径都包含至少 $k$ 个黑点. 把第 $i$ 个点染黑需要代价 $a_i$.
网络流, 竟然没看出来. (这是当时听完 sxy 的讲解后我的感叹)
但是半年后的今天, 我对着电脑从上午看到天黑也不懂是如何流, 直到委托一位人脉广泛的同学搞到了不知道哪里来的 STD, 我一看它把一个点拆成 $2k$ 个就开始意识到事情的不对劲, 然后才发现 $k \leq 5$.
然后按 STD 的意思把图建出来, 血压就上来了, 它里面有一组边, 是这样的:
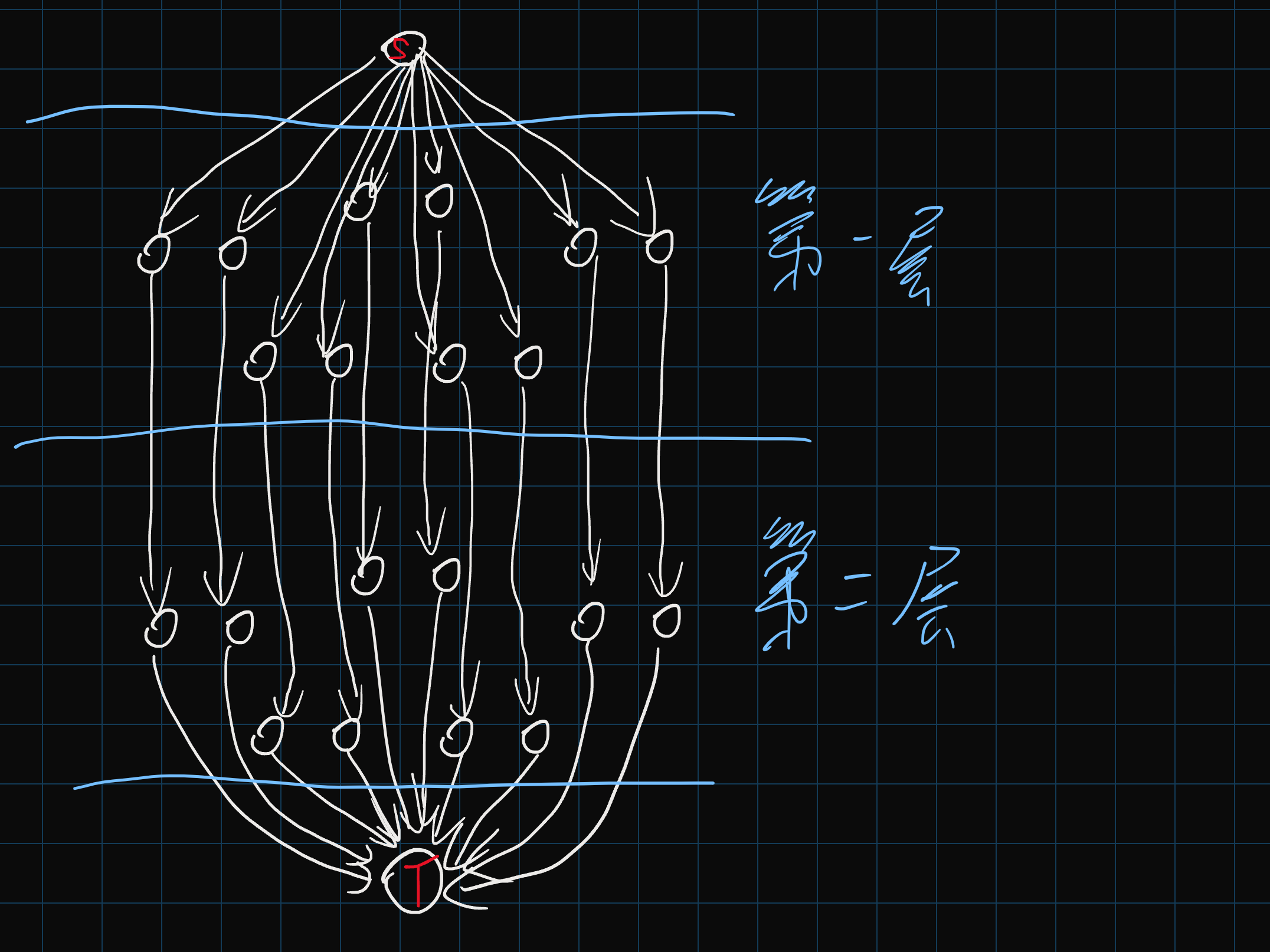
里面所有白色边的容量都是 $\infin$, 那我就不满意了, 你连这些边除了给最大流增加了 $2n\infin$ 以外还有什么意义吗? 这个方案为了防止两种 (蓝色和白色) $\infin$ 互相冲突, 使用 $\infin^2$ 来表示蓝色的更大的 $\infin$.
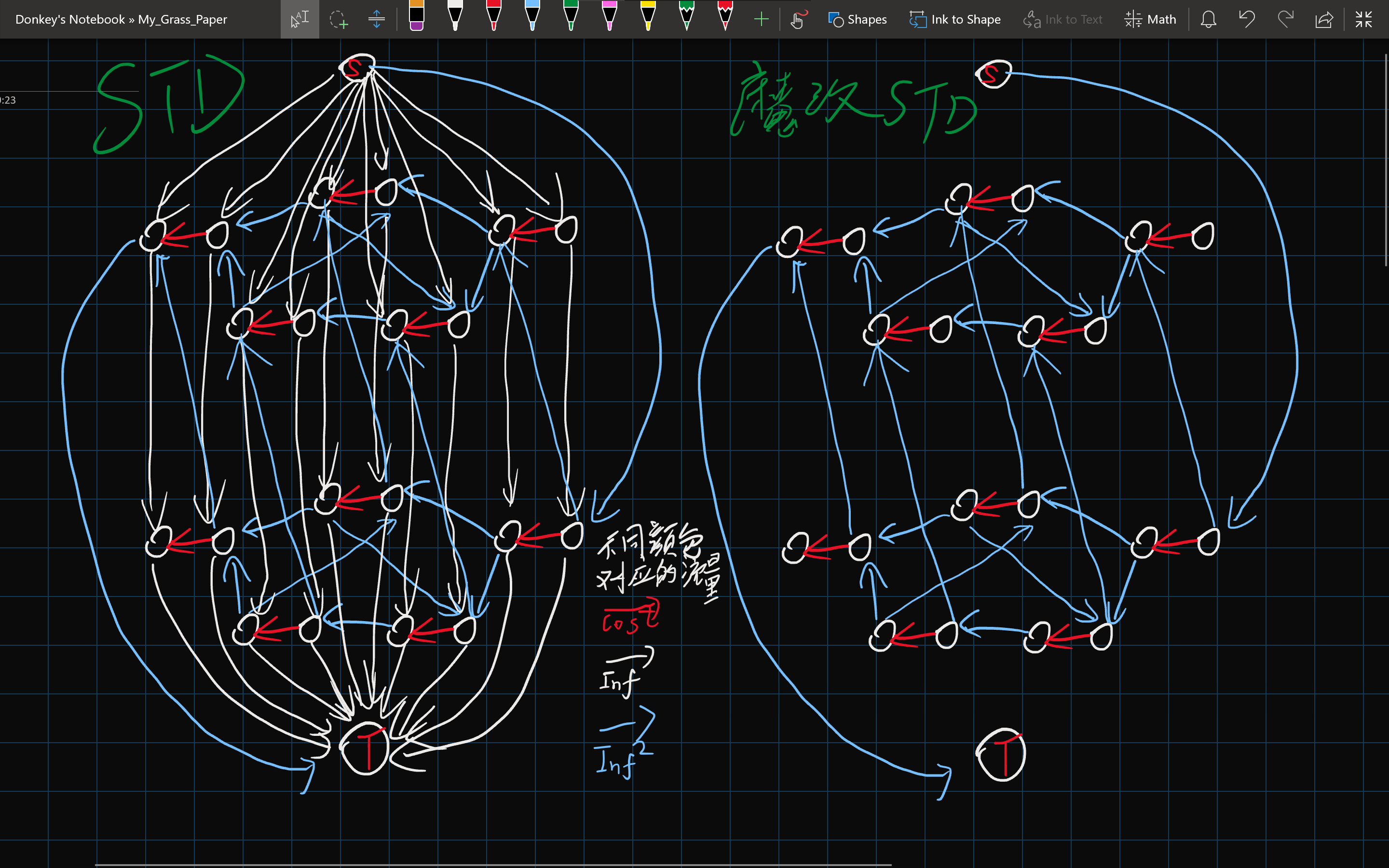
花了一个多小时对着这个连边方式发呆, 所以我便把这些边去掉能怎么样呢? 我把 STD 里所有这一类的边都删了, 给最大流一个 $2n\infin$ 的修正, 发现貌似确实和我设想的一样, 结果完全相同. 交上去 `WA on 1`, 人傻了, 发现在无解的时候, 之前的连边方式确实能返回一个非常大的最大流, 可以通过最大流过大来判断无解. 我登时便不高兴了起来, 我虽然不会求答案, 但起码会判无解, 这题目欺人太甚. 所以便写了一个 BFS, 把起点到终点最短路小于 $k$ 的输入都判了无解.
看着程序欢快地跑了十几个点, 我十分欣慰, 觉得至少没有太大的锅. 程序跑了五十多个点了, 我觉得哇不会过了吧, 要是过了这题解就太没正事了, 我给它删了这么多边都能跑这么多. 看着程序嗖嗖嗖跑到八九十个点, 我心想果然我还是牛逼, 这么轻松就优化了 STD 一大截. 但是当结果停留在 `WA on 114` 的时候, 我先是呆住了, 然后希望能够看到错误的测试点, 当发现我的 Rating 不足以满足代码的美好偷点的需要时, 我真想在这个结果后面补全后一半 `WA on 514`, 可惜它没有这么多点. 仍然是那位人脉广泛的同学帮我找了一位橙名大佬, 帮我交了程序, 偷到了点, 发现我魔改的时候, 输出方案的地方 $i$ 多枚举了一倍, 属于是没改干净. 这种傻逼程序都能过 $113$ 个点才是出题人应该好好反思的事情.
两三下改过来再次提交, 仍然是跑到了一百多个点, 在我心想这个题点怎么这么多, 并且准备好迎接那喜闻乐见的 `Accepted` 的时候, `WA on 178` 把我拉回了现实. 靠着人脉再次投到点的时候, 我发现这个点 $k = 1$, 但是答案却染黑了 $0$ 个点. 正当我抱怨这个申必出题人为什么要写这种垃圾 STD 还不审查自己的程序的时候, 橙名大佬告诉我这个点图不连通, 所以无需染黑任何点, 就可以满足从起点到终点的 $0$ 条路径没有一条黑点少于 $1$, 我恍然大悟, 连忙加一句特判, 便再次提交. 程序跑到两百多个点的时候, 一切都那么梦幻, 我不能相信一个 STD 可以如此故弄玄虚, 也不能相信自己这么轻松就在不影响正确性的前提下抠掉了这么多边. 跑到两百八十多个点之后, 绿色的文字亮了起来, 我也忘了是 `Accepted` 还是 CF 整的花活 `Happy New Year!`, 反正就是过了.
接下来说一下这个题的建模, 如上面图中 `魔改 STD` 所示. 先考虑 $k = 1$ 的情况, 我们把一个点拆成两个, 两点之间连一条边 (二号点连向一号点), 容量是 $a_i$, 把原图中的边 $(u, v)$ 的容量赋为 $\infin$, 从 $v$ 的一号点连向 $u$ 的二号点. 从源点向终点的二号点一条 $\infin$ 的边, 从起点的一号点连向汇点一条 $\infin$ 的边. 跑出来的最大流就是最小割, 而最小割的边所属的原图中的点便是所选的点, 根据最小割的定义, 任何连接起点和终点的路径都可以经过一条割上的点, 且最小割是最小的割, 因此符合要求.
当 $k > 1$ 时, 我们把图复制成 $k$ 层, 每一层都是一个 $k = 1$ 情况下的网络, 在相邻两层之间连边, 第 $i + 1$ 层的 $j$ 点的二号点, 向第 $i$ 层的 $j$ 点的一号点连 $\infin$ 的边. 源点只向最后一层的终点的二号点连边, 只有第一层起点的一号点向汇点连边. 这就引出了 STD 的又一个槽点, 你好好连正向边不行吗? 非要连什么反向边, 不是膈应人是什么, 像下面这样连有何不可?
改用正常的连边方式, 考虑这样做的正确性. 我们求出了最小割, 并且把这些最小割边删掉, 表示不能走. 而层间的边就相当于是跳过禁止通行的边的机会, 当我遇到一个割边, 我可以走层间的边绕过它. 因为层间的边只能往下走, 且只有 $k$ 层, 所以我们一共可以跳过 $k - 1$ 个黑点. 如果即使是这样都不能找到到汇点的增广路, 那么说明任何路径的黑点至少有 $k$ 个.
下面是代码 (不是魔改 STD, 那玩意改了也膈应人):
```cpp
unsigned a[205], m, n;
unsigned A, B, C, D, t, S, T, k;
unsigned Cnt(0), Ans[205], Tmp(0);
struct Node;
struct Edge {
Node* To;
unsigned Pos, Con;
};
struct Pr {
vector <Pr*> E;
unsigned Dep;
}P[205], * Stack[205], ** Hd(Stack), ** Tl(Stack);//其实是队列, 为了防止重名所以才叫 Stack
struct Node {
vector<Edge> E;
unsigned Dep;
}N[2005], * Que[2005], ** QH(Que), ** QT(Que);
inline char BFS() {
for (unsigned i(1); i <= Cnt; ++i) N[i].Dep = 0xffffffff;
QH = QT = Que, (*(++QT) = N)->Dep = 0;
while (QH != QT) {
Node* Cur(*(++QH));
for (auto i : Cur->E) if ((i.Con) && (i.To->Dep >= 0xffffffff)) i.To->Dep = Cur->Dep + 1, * (++QT) = i.To;
}
return N[Cnt].Dep < 0xffffffff;
}
inline unsigned DFS(Node* x, unsigned Come) {
if (x == N + Cnt) return Come;
unsigned Gone(0), Push(0);
for (unsigned i(x->E.size() - 1); (~i) && Come; --i) if (x->E[i].Con && (x->E[i].To->Dep > x->Dep)) {
Push = min(Come, x->E[i].Con);
Push = DFS(x->E[i].To, Push);
x->E[i].Con -= Push, Come -= Push;
x->E[i].To->E[x->E[i].Pos].Con += Push, Gone += Push;
}
return Gone;
}
signed main() {
n = RD(), m = RD(), k = RD(), S = RD(), T = RD();
for (unsigned i(1); i <= n; ++i) {
a[i] = RD(), P[i].Dep = 0xffffffff;
for (unsigned j(0); j < k; ++j)
N[((j * n + i) << 1) - 1].E.push_back((Edge) { N + ((j * n + i) << 1), N[(j * n + i) << 1].E.size(), a[i] });
for (unsigned j(0); j < k; ++j)
N[(j * n + i) << 1].E.push_back((Edge) { N + ((j * n + i) << 1) - 1, N[((j * n + i) << 1) - 1].E.size() - 1, 0 });
for (unsigned j(1); j < k; ++j)
N[(((j - 1) * n + i) << 1) - 1].E.push_back((Edge) { N + ((j * n + i) << 1), N[(j * n + i) << 1].E.size(), 0xffffffff });
for (unsigned j(1); j < k; ++j)
N[(j * n + i) << 1].E.push_back((Edge) { N + (((j - 1) * n + i) << 1) - 1, N[(((j - 1) * n + i) << 1) - 1].E.size() - 1, 0 });
}
N[0].E.push_back((Edge) { N + (S << 1) - 1, N[(S << 1) - 1].E.size(), 0xffffffff });
N[(S << 1) - 1].E.push_back((Edge) { N, N->E.size() - 1, 0 });
N[(n * (k - 1) + T) << 1].E.push_back((Edge) { N + (Cnt = ((n * k) << 1) + 1), N[((n * k) << 1) + 1].E.size(), 0xffffffff });
N[Cnt].E.push_back((Edge) { N + ((n * (k - 1) + T) << 1), N[(n * (k - 1) + T) << 1].E.size() - 1, 0 });
for (unsigned i(1); i <= m; ++i) {
A = RD(), B = RD();
P[A].E.push_back(P + B);
for (unsigned j(0); j < k; ++j) {
N[(n * j + A) << 1].E.push_back((Edge) { N + ((n * j + B) << 1) - 1, N[((n * j + B) << 1) - 1].E.size(), 0xffffffff });
N[((n * j + B) << 1) - 1].E.push_back((Edge) { N + ((n * j + A) << 1), N[(n * j + A) << 1].E.size() - 1, 0 });
}
}
(*(++Tl) = P + S)->Dep = 1;
while (Hd != Tl) {
Pr* Cur(*(++Hd));
for (auto i : Cur->E) if (i->Dep >= 0xffffffff) *(++Tl) = i, i->Dep = Cur->Dep + 1;
}
if (P[T].Dep < k) { printf("-1\n"); return 0; }
if (P[T].Dep >= 0xffffffff) { printf("0\n"); return 0; }
while (BFS()) DFS(N, 0xffffffff);
Cnt = 0;
for (unsigned i(1); i <= n; ++i) for (unsigned j(0); j < k; ++j)
if ((N[(j * n + i) << 1].Dep >= 0xffffffff) && (N[((j * n + i) << 1) - 1].Dep < 0xffffffff)) { Ans[++Cnt] = i; break; }
printf("%u\n", Cnt);
for (unsigned i(1); i <= Cnt; ++i) printf("%u ", Ans[i]);
return Wild_Donkey;
}
```
### B
给一个边带权无向图, 从 $0$ 号点出发, 可以在任意时刻掉头 (当然包括一条边上), 每天最少走 $L$ 单位, 最多走 $U$ 单位, 要求每天必须在 $0$ 号点结束. 如果每天必须经过至少一条之前从未经过的边, 否则结束过程. 问最多跑多少天.
由于每条路可以从任意位置调头, 所以只要在一条边上反复横跳就可以凑出任何长度, 所以下界形同虚设, 如果一条路径不合法, 任意地方迂回两步就凑够了.
所以只要保证在上界范围内, 走出去能回得来就行了, 所以一条边可以经过当且仅当它的一个端点到 $0$ 点的最短路比上界的一半要小即可.
对于使答案最大, 我们一定每次只探索一条边, 为了达到下界, 我们在起点附近迂回. 所以最后答案就是所有能到达的边数.
跑最短路即可, ACM 可以直接复制板子.
```cpp
unsigned a[10005], m, n, Cnt(0), A, B, C, D, t, Ans(0), Tmp(0);
char b[10005];
struct Edge;
struct Node {
unsigned Dis;
Edge *Fst;
char InQue;
}N[100005];
struct Edge {
unsigned Val;
Node *To;
Edge *Nxt;
}E[400005], *CntE(E);
void Link(Node *x, Node *y) {
(++CntE)->Nxt = x->Fst;
x->Fst = CntE;
CntE->To = y;
CntE->Val = C;
}
struct Pnt{
Node *P;
unsigned Dist;
const inline char operator <(const Pnt &x) const{
return this->Dist > x.Dist;
}
}TmpP;
priority_queue<Pnt> Q;
int main() {
n = RD(), m = RD(), RD(), D = RD();
for (register unsigned i(1); i <= m; ++i) {
A = RD(), B = RD(), C = RD();
Link(N + A, N + B);
Link(N + B, N + A);
}
for (register unsigned i(1); i <= n; ++i) {
N[i].Dis = 0x3f3f3f3f;
}
N[0].Dis = 0, TmpP.P = N, Q.push(TmpP);
while (Q.size()) {
register Node *Now((Q.top()).P); Q.pop();
if(Now->InQue) continue;
Now->InQue = 1;
Edge *Sid(Now->Fst);
while (Sid) {
if(Sid->To->Dis > Now->Dis + Sid->Val) {
Sid->To->Dis = Now->Dis + Sid->Val;
TmpP.Dist = Sid->To->Dis, TmpP.P = Sid->To, Q.push(TmpP);
}
Sid = Sid->Nxt;
}
}
for (register unsigned i(1); i <= m; ++i) {
if((min((E[i << 1].To)->Dis, (E[(i << 1) - 1].To)->Dis) << 1) < D) {
++Ans;
}
}
printf("%u\n", Ans);
return Wild_Donkey;
}
```
### C
最签到题, 给 $n$ 种需要的原料分别的需求量和持有量, 求一共能生产多少产品.
我们可以给每个原料持有量除以需求量下取整取最小值. 轻松写意又从容.
```cpp
unsigned a[10005], m, n, Cnt(0), A, B, C, D, t, Ans(0x3f3f3ff3), Tmp(0);
char b[10005];
int main() {
n = RD();
for (register unsigned i(1); i <= n; ++i) {
A = RD(), B = RD();
Ans = min(Ans, B/A);
}
printf("%u\n", Ans);
return Wild_Donkey;
}
```
### E
赛时设计的 $O(n^3)$ 状态 $O(1)$ 转移的奇妙 DP, $f_{i, j, k}$ 表示前 $i$ 个音符, 击打 $j$ 个, 到 $i$ 为止连击 $k$ 次的最大收益.
但是非常遗憾, 它的状态复杂度就注定了没有前途.
而正解则是两维 $f_{i, j}$ 表示了考虑前 $i$ 个音符, 漏掉了 $j$ 个的最大收益. 转移 $O(n)$. 为了方便表示, 我们用 $g_{k, i}$ 预处理 $[k, i]$ 连击的收益.
$$
f_{i, j} = max(f_{k - 2, j - 1} + g_{k, i})
$$
但是很遗憾这还是 $O(n^3)$ 的复杂度.
打表得到这个 DP 满足四边形不等式, 可以决策单调性优化, 所以可以二分转移, 总复杂度 $O(n^2 \log n)$.
### F
给 $n$ 行字符串, 按每行出现的次数和出现顺序排序, 按顺序输出出现次数最大的 $m$ 个本质不同的行, 如果有相同出现次数的, 优先输出出现晚的. 如果本质不同的行不足 $m$ 个, 则按顺序输出全部.
复杂度 $O(wn \log n)$, 大概 $8 * 10^7$, 能过. (不过大水题写那么长确实非常丢脸)
```cpp
struct Str {
char b[55];
unsigned Rak;
inline const char operator < (const Str &x) const {
register char i(1);
while ((this->b[i] == x.b[i]) && (this->b[i] > 20)) {
++i;
}
if(this->b[i] == x.b[i]) {
return this->Rak < x.Rak;
}
return this->b[i] < x.b[i];
}
inline const char operator == (const Str &x) const {
register char i(1);
while (this->b[i] == x.b[i] && (this->b[i] > 20)) {
++i;
}
return this->b[i] == x.b[i];
}
}S[100005];
struct Pos {
unsigned P;
inline const operator < (const Pos &x) const{
return S[this->P].Rak > S[x.P].Rak;
}
};
vector<Pos> V[100005];
unsigned m, n, Cnt(0), A, B, C, D, t, Ans(0), Tmp(0);
char Ch(0);
int main() {
n = RD() * 3, m = RD();
for (register unsigned i(1), j(0); i <= n; ++i) {
j = 0;
do {
S[i].b[++j] = getchar();
}while(S[i].b[j] > 20);
S[i].Rak = i;
}
sort(S + 1, S + n + 1);
Cnt = 1;
for (register unsigned i(2); i <= n + 1; ++i) {
register Pos O;
if(S[i - 1] == S[i]) {
++Cnt;
} else {
O.P = i - 1;
V[Cnt].push_back(O);
Cnt = 1;
}
}
for (register unsigned i(n); i; --i) {
if(V[i].size()) {
sort(V[i].begin(), V[i].end());
if(V[i].size() <= m) {
for (register unsigned j(0); j < V[i].size(); ++j) {
printf("%s", (S[V[i][j].P].b) + 1);
}
m -= V[i].size();
} else {
for (register unsigned j(0); j < m; ++j) {
printf("%s", (S[V[i][j].P].b) + 1);
}
m = 0;
}
}
if(!m) break;
}
return Wild_Donkey;
}
```
### G
要求在平面内放 $n$ 个整点, 连 $m$ 条边, 构造 $k$ 个闭合的面.
首先前置欧拉公式:
$$
V - E + F = 1 + 连通块个数
$$
因为已经输入了 $V$, $E$, $F$ 所以可以求出连通块个数 $L$.
选择构造 $L - 1$ 个单点, 剩下 $V - L + 1$ 个点, $E$ 条边组成一个平面图.
$n$ 个点的平面图最多有 $3n - 6$ 条边, 需要构造 $V$ 个点, $E$ 条边的平面图.
构造方式是先取 $3$ 个点的平面图, 每次在外面加一个点, 往凸包上三个点连边.
由于 $V \geq 3$ 的边最多的平面图一定是三角形, 所以选一个棋盘内最大的三角形作为轮廓.
然后构造边最多的平面图, 每加入一个点连三条边, 直到可分配边数和可分配点数相同, 然后在图上挂链, 每加一个点连一条边.
### H
棋盘上有一些点, 要求在棋盘内从 $(0, 0)$ 走到 $(x, y)$, 求路径和每个点的最短距离的最大值.
这个题很容易想到二分, 但是判定一个二分的半径是否可行成了需要考虑的最大问题.
将两点之间不能走抽象为两点之间连边, 而连边的条件就是两点距离的一半小于等于二分的半径. 其意义不是通路, 而是防止经过的墙壁.
左边界和上边界可以抽象成一个点, 右边界和下边界也可以抽象成一个点. 那么从左上往右下走, 如果存在一条通路, 则这条通路已经将棋盘分割成左下和右上两个部分, 不能互相到达, 所以只要判断按照二分的距离连边, 左上右下两个点是否连通即可.
但是如果是二分 $10^6$ 并且得到 $10^{-5}$ 的精度, 最坏需要二分 $\log_2 10^{11}$ 次, 需要 $36$ 次, 而本题有 $1000$ 个点, 每次判定是 $O(n^2)$, 而 $3.6 * 10^7$ 的浮点数比较会比较悬.
我们发现答案一定是某一对点的距离, 因为如果不是两个点的距离, 那么对答案进行细微的扰动是不会影响任何边的连接情况的, 也就不会改变连通性. 所以我们只要将所有边权离散后二分所有存在的边权即可, 最劣次数是 $\log_2 10^6 = 20$ 次.
而判连通性也没必要提前连边, 我们只要在 DFS 过程中现判断一个点能否到达即可. 这就不至于每次判定会将 $O(n^2)$ 跑满了.
所以优化到带剪枝的 $O(n^2 \log n^2)$ 就可以稍微放心地提交了.
```cpp
float W, H, Pos[1005][2], Dist[1005][1005], Tmp[520005], Frtr;
unsigned a[1005][1005], m, n, Cnt(0), A, B, C, D, t, Ans(0);
char Vis[1005], Flg;
inline float Dis (unsigned x, unsigned y) {
register float X(Pos[x][0] - Pos[y][0]), Y(Pos[x][1] - Pos[y][1]);
return sqrt((X * X) + (Y * Y));
}
void DFS(unsigned x) {
Vis[x] = 1;
if(x == n + 1) {
Flg = 1;
return;
}
for (register unsigned i(0); i <= n + 1; ++i) {
if((!(Vis[i])) && (Dist[x][i] <= Frtr)) {
DFS(i);
}
}
return;
}
int main() {
scanf("%f%f", &W, &H);
n = RD();
Dist[0][0] = 10000000;
for (register unsigned i(1); i <= n; ++i) {
scanf("%f%f", &Pos[i][0], &Pos[i][1]);
Dist[i][i] = 10000000;
Dist[0][i] = Dist[i][0] = Tmp[++Cnt] = min(Pos[i][0], H - Pos[i][1]);
Dist[n + 1][i] = Dist[i][n + 1] = Tmp[++Cnt] = min(Pos[i][1], W - Pos[i][0]);
}
Dist[n + 1][0] = Dist[0][n + 1] = 10000000;
for (register unsigned i(2); i <= n; ++i) {
for (register unsigned j(1); j < i; ++j) {
Tmp[++Cnt] = Dist[i][j] = Dist[j][i] = Dis(j, i) / 2;
}
}
sort(Tmp + 1, Tmp + Cnt + 1);
Cnt = unique(Tmp + 1, Tmp + Cnt + 1) - Tmp - 1;
register unsigned L(1), R(Cnt), Mid;
while (L ^ R) {
Mid = ((L + R) >> 1);
Flg = 0;
memset(Vis, 0, sizeof(Vis));
Frtr = Tmp[Mid];
DFS(0);
if(Flg) {
R = Mid;
} else {
L = Mid + 1;
}
}
printf("%.6f\n", Tmp[L]);
return Wild_Donkey;
}
```
但是我们仍然可以继续优化, 将所有边按连接权值从小到大排序, 利用类似 Kruskal 的方法每次连接最小的边, 然后判 $0$ 到 $n + 1$ 的连通性, 然后使用并查集维护连通性即可. 答案就是连通的时候最后加入的边权. 这样虽然时间仍然是 $O(n^2 \log n^2)$, 但是对于随机数据, `sort` 的期望复杂度往往更接近线性.
### I
是 Nim 游戏的板子, 每个横着的格子中间的空地可以看成是石子, 每个横着的格子看作一堆石子. (貌似可以证明, 但是我不会, 之后应该会有专门的博客来证吧)
这样就可以将所有长度 $-2$ 之后的值异或起来. 结果为 $0$ 则先手必败, 否则必胜, 因为先手总能将局面变成异或起来为 $0$ 的局面, 使得对手变成必败态.
令人难受的是, 场上推了 $2H$ 的式子和结论, 甚至打了好几把这个游戏, 如果最后不知道是 Nim 博弈, 我们都准备将这个游戏作为茶余饭后的消遣小游戏了...
```cpp
unsigned a[10005], m, n, Cnt(0), A, B, C, D, t, Ans(0), Tmp(0);
char b[10005];
int main() {
n = RD();
for (register unsigned i(1); i <= n; ++i) {
Ans ^= RD() - 2;
}
scanf("%s", b + 1);
if(Ans) Ans = 1;
if(b[1] == 'W') {
++Ans;
}
printf((Ans & 1) ? "Blackking\n" : "Whiteking\n");
return Wild_Donkey;
}
```
### K
给两个矩阵, 按要求取反点, 使得第二个矩阵和第一个相同.
每个矩阵保证:
- 边界的一圈同色
- 联通的定义是四连通, 不存在 $\frac {*|.}{.|*}$ 或 $\frac {.|*}{*|.}$ 的情况
- 保证每个连通块最多只相邻两个连通块, 对于边界连通块, 仅相邻一个连通块
要求翻转过程中, 不出现连通块数量和相邻关系改变的情况, 任何时刻的矩阵都要满足输入的三个条件.
发现符合要求的局面一定是一个连通块套另一个连通块...以此类推.
所以可以使用 BFS 找出连通块和相邻关系, 这样就能很方便地判解的有无, 然后将其抽象为一个一圈一圈的图. 每圈代表一个连通块.
因为一个点可以反转多次, 所以不妨先将两个矩阵变换到理想的中间态, 然后将第一个矩阵的变换序列反转, 拼到第二个矩阵的序列后面就是答案.
而变换到中间态也很简单, 只要从外到内, 一格一格扩张到自己该到达的边界即可. (注意只扩展那些不会产生新连通块的格子)
## Day27: 模拟赛
### A
给一个 DAG, 要求有序对 $(a, b)$ 使得存在一个 $c$, 既能到达 $a$, 又能到达 $b$. 数据保证点的编号就是拓扑序.
首先想到的是将所有入度为 $0$ 的点作为 $c$, 因为如果对于点对 $(a, b)$ 的 $c$, 能连向它的点一定也能做这个 $c$. 所以合法答案中所有点对的 $c$ 都可以是一个入度为 $0$ 的点.
将从某个 $c$ 出发能到达的所有点存到一个数组中, 然后 $O(n^2)$ 得到所有点对, 将对应的二维数组的位置置为 $1$.
$O(n)$ 个源点, 每个源点 $O(n^2)$ 扫描, 复杂度 $O(n^3)$.
`70'.cpp`
```cpp
unsigned List[3005], Hd(0), Tl(0), m, n, Cnt(0), A, B, C, D, t, Ans(0), Tmp(0);
char b[3005][3005];
struct Edge;
struct Node {
Edge *Fst;
unsigned Deg, Topo, Vis, Size, Tms;
}N[3005];
struct Edge {
Node *To;
Edge *Nxt;
}E[3005];
unsigned DFS1 (Node *x) {
List[++Cnt] = x - N;
register Edge *Sid(x->Fst);
if(!Sid) {
return 1;
}
register unsigned TmSz(1);
while (Sid) {
if(!(Sid->To->Vis)) {
Sid->To->Vis = 1;
TmSz += DFS1(Sid->To);
}
Sid = Sid->Nxt;
}
}
inline void Clr() {
memset(b, 0, sizeof(b));
memset(N, 0, sizeof(N));
memset(E, 0, sizeof(E));
Ans = 0;
}
int main() {
t = RD();
for (register unsigned T(1); T <= t; ++T){
Clr();
n = RD(), m = RD();
for (register unsigned i(1); i <= m; ++i) {
A = RD(), B = RD();
E[i].Nxt = N[A].Fst;
N[A].Fst = E + i;
++(N[B].Deg);
E[i].To = N + B;
}
for (register unsigned i(1); i <= n; ++i) {
if(!(N[i].Deg)) {
Cnt = 0;
DFS1(N + i);
for (register unsigned j(1); j <= n; ++j) {
N[j].Vis = 0;
}
for (register unsigned j(1); j <= Cnt; ++j) {
b[List[j]][List[j]] = 1;
for (register unsigned k(j + 1); k <= Cnt; ++k) {
b[List[j]][List[k]] = b[List[k]][List[j]] = 1;
}
}
}
}
for (register unsigned i(1); i <= n; ++i) {
for (register unsigned j(1); j <= n; ++j) {
Ans += b[i][j];
}
}
printf("%u\n", Ans);
}
return Wild_Donkey;
}
```
正解考虑 DP, 发现有一个条件还没使用, 就是点的拓扑序是编号. 设布尔变量 $f_{i, j}$ 表示 $(i, j)$ 点对合法.
接下来枚举 $i$, $j$ 转移即可, 因为只要 $(i, j)$ 合法, 那么对于任何 $i$ 能到达的 $i'$, $j$ 能到达的 $j'$, 都有 $(i', j')$ 合法.
所以按拓扑序转移即可. 复杂度 $O(n(n + m))$.
```cpp
unsigned m, n, Cnt(0), A, B, C, D, t, Ans(0);
char f[3005][3005];
struct Edge {
unsigned To;
Edge *Nxt;
}E[3005], *Fst[3005];
inline void Clr() {
memset(f, 0, sizeof(f));
memset(Fst, 0, sizeof(Fst));
Ans = 0;
}
int main() {
t = RD();
for (register unsigned T(1); T <= t; ++T){
Clr();
n = RD(), m = RD();
for (register unsigned i(1); i <= m; ++i) {
A = RD(), B = RD();
E[i].Nxt = Fst[A];
Fst[A] = E + i;
E[i].To = B;
}
for (register unsigned i(1); i <= n; ++i) {
f[i][i] = 1;
for (register unsigned j(1); j <= n; ++j) {
if(f[i][j]) {
++Ans;
register Edge *Sid(Fst[j]);
register unsigned Son;
while (Sid) {
Son = Sid->To;
f[i][Son] = f[Son][i] = f[j][Son] = f[Son][j] = 1;
Sid = Sid->Nxt;
}
}
}
}
printf("%u\n", Ans);
}
return Wild_Donkey;
}
```
### B
每个物品可以放到 $a_i$ 筐中, 也能放到 $b_i$ 筐中. 求如何使得筐中有奇数物品的筐最小.
每个筐看作一个点, 每个物品当作一条边, 连接 $a_i$, $b_i$. 对于一个连通块, 我们尝试将有端点相同的节点配对然后同时删除, 意义是将两个物品同时放入一个筐中, 发现存在策略使得连通块最后只剩 $0$ 或 $1$ 条边.
删边策略是: 以任意点为根生成一棵 DFS 树, 这棵树存在三种边, 树边, 自环边, 回边 (树边如果有重边, 则除了第一次经过的树边, 其余算作回边), 从叶子开始考虑. 对于一个叶子, 如果它的自环边和回边数量是偶数, 就直接将自环边和回边删除, 否则删除的同时还要带上连接父亲的边. 考虑完叶子回溯到它的父亲 $x$, 这时 $x$ 可能连着 $4$ 种边, 连接 $x$ 的父亲的树边, 连接 $x$ 的儿子的树边, 回边, 自环边. 因为这时如果还有儿子边, 儿子就只剩一个单点了, 讨论后三种边的数量, 如果是偶数就直接删除, 如果是奇数就带上连接父亲的树边. 这样每次讨论一个点就必定删除偶数条边, 到了根, 如果出现了需要带上连接父亲边的情况, 这时删除偶数条边后, 会剩下一条.
这种只剩一条边的情况出现, 唯一的条件是连通块的总边数是奇数. 所以我们只要统计每个连通块的边数 $\And 1$ 的总和即可.
```cpp
unsigned m, n, Cnt(0), A, B, Ans(0);
struct Edge;
struct Node {
Edge *Fst;
char Vis;
}N[200005];
struct Edge {
Node *To;
Edge *Nxt;
}E[400005], *CntE(E);
void Link(Node *x, Node *y) {
(++CntE)->Nxt = x->Fst;
x->Fst = CntE;
CntE->To = y;
}
void DFS(Node *x) {
x->Vis = 1;
register Edge *Sid(x->Fst);
while (Sid) {
++Cnt;
if(!(Sid->To->Vis)) {
DFS(Sid->To);
}
Sid = Sid->Nxt;
}
}
int main() {
n = RD(), m = RD();
for (register unsigned i(1); i <= n; ++i) {
A = RD(), B = RD();
Link(N + A, N + B);
Link(N + B, N + A);
}
for (register unsigned i(1); i <= m; ++i) {
if(!N[i].Vis) {
Cnt = 0;
DFS(N + i);
Ans += ((Cnt >> 1) & 1);
}
}
printf("%u\n", Ans);
}
```
与此同时, 不建图, 仅用并查集维护连通块, 貌似可以得到更优的常数.
### C
$f_{a_1, a_2, a_3, a_4}$ 代表已经选了 $a_1$ 个 $2$, $a_2$ 个 $3$, $a_3$ 个 $4$, $a_4$ 个 $5$ 的最少纸币.
我们知道对于 $f_{a_1, a_2, a_3, a_4}$ 的答案中, 前 $a_1 + a_2 + a_3 + a_4$ 种纸币凑出了 $n \% (2^{a_1}3^{a_2}4^{a_3}5^{a_4})$ 的钱, 剩下的钱用 $\frac{n}{2^{a_1}3^{a_2}4^{a_3}5^{a_4}}$ 张第 $a_1 + a_2 + a_3 + a_4 + 1$ 种纸币凑出.
转移要枚举本次选哪个数, 然后转移即可.
$$
\begin{aligned}
&f_{a_1, a_2, a_3, a_4} = min(\\
&f_{a_1 - 1, a_2, a_3, a_4} - \frac{n}{2^{a_1 - 1}3^{a_2}4^{a_3}5^{a_4}} + \frac{n}{2^{a_1 - 1}3^{a_2}4^{a_3}5^{a_4}} \% 2,\\
&f_{a_1, a_2 - 1, a_3, a_4} - \frac{n}{2^{a_1}3^{a_2 - 1}4^{a_3}5^{a_4}} + \frac{n}{2^{a_1}3^{a_2 - 1}4^{a_3}5^{a_4}} \% 3,\\
&f_{a_1, a_2, a_3 - 1, a_4} - \frac{n}{2^{a_1}3^{a_2}4^{a_3 - 1}5^{a_4}} + \frac{n}{2^{a_1}3^{a_2}4^{a_3 - 1}5^{a_4}} \% 4,\\
&f_{a_1, a_2, a_3, a_4 - 1} - \frac{n}{2^{a_1}3^{a_2}4^{a_3}5^{a_4 - 1}} + \frac{n}{2^{a_1}3^{a_2}4^{a_3}5^{a_4 - 1}} \% 5\\
&) + \frac{n}{2^{a_1}3^{a_2}4^{a_3}5^{a_4}}
\end{aligned}
$$
但是细节有亿点点多, 所以有了这般地狱绘图:
```cpp
unsigned long long g[70][70][70][70], f[70][70][70][70];
unsigned long long m, Ans(0x3f3f3f3f3f3f3f3f), Tmp;
int main() {
g[0][0][0][0] = RD(), m = RD() - 1;
for (register unsigned i(1); i <= m; ++i) {
g[i][0][0][0] = g[i - 1][0][0][0] / 2;
g[0][i][0][0] = g[0][i - 1][0][0] / 3;
g[0][0][i][0] = g[0][0][i - 1][0] / 4;
g[0][0][0][i] = g[0][0][0][i - 1] / 5;
if(!g[i][0][0][0]) break;
for (register unsigned j(1); j + i <= m; ++j) {
g[i][j][0][0] = g[i][j - 1][0][0] / 3;
g[i][0][j][0] = g[i][0][j - 1][0] / 4;
g[i][0][0][j] = g[i][0][0][j - 1] / 5;
g[0][i][j][0] = g[0][i][j - 1][0] / 4;
g[0][i][0][j] = g[0][i][0][j - 1] / 5;
g[0][0][i][j] = g[0][0][i][j - 1] / 5;
if(!g[i][j][0][0]) break;
for (register unsigned k(1); k + j + i <= m; ++k) {
g[i][j][k][0] = g[i][j][k - 1][0] / 4;
g[i][j][0][k] = g[i][j][0][k - 1] / 5;
g[i][0][j][k] = g[i][0][j][k - 1] / 5;
g[0][i][j][k] = g[0][i][j][k - 1] / 5;
if(!g[i][j][k][0]) break;
for (register unsigned l(1); l + k + j + i <= m; ++l) {
g[i][j][k][l] = g[i][j][k][l - 1] / 5;
if(!g[i][j][k][l]) break;
}
}
}
}
memset(f, 0x3f, sizeof(f));
f[0][0][0][0] = g[0][0][0][0];
for (register unsigned i(1); i <= m; ++i) {
if(!g[i][0][0][0]) break;
f[i][0][0][0] = min(f[i][0][0][0], f[i - 1][0][0][0] - g[i - 1][0][0][0] + g[i - 1][0][0][0] % 2 + g[i][0][0][0]);
f[0][i][0][0] = min(f[0][i][0][0], f[0][i - 1][0][0] - g[0][i - 1][0][0] + g[0][i - 1][0][0] % 3 + g[0][i][0][0]);
f[0][0][i][0] = min(f[0][0][i][0], f[0][0][i - 1][0] - g[0][0][i - 1][0] + g[0][0][i - 1][0] % 4 + g[0][0][i][0]);
f[0][0][0][i] = min(f[0][0][0][i], f[0][0][0][i - 1] - g[0][0][0][i - 1] + g[0][0][0][i - 1] % 5 + g[0][0][0][i]);
}
for (register unsigned i(1); i <= m; ++i) {
if(!g[i][0][0][0]) break;
for (register unsigned j(1); j + i <= m; ++j) {
if(!g[i][j][0][0]) break;
f[i][j][0][0] = min(f[i][j][0][0], f[i][j - 1][0][0] - g[i][j - 1][0][0] + g[i][j - 1][0][0] % 3 + g[i][j][0][0]);
f[i][j][0][0] = min(f[i][j][0][0], f[i - 1][j][0][0] - g[i - 1][j][0][0] + g[i - 1][j][0][0] % 2 + g[i][j][0][0]);
f[i][0][j][0] = min(f[i][0][j][0], f[i][0][j - 1][0] - g[i][0][j - 1][0] + g[i][0][j - 1][0] % 4 + g[i][0][j][0]);
f[i][0][j][0] = min(f[i][0][j][0], f[i - 1][0][j][0] - g[i - 1][0][j][0] + g[i - 1][0][j][0] % 2 + g[i][0][j][0]);
f[i][0][0][j] = min(f[i][0][0][j], f[i][0][0][j - 1] - g[i][0][0][j - 1] + g[i][0][0][j - 1] % 5 + g[i][0][0][j]);
f[i][0][0][j] = min(f[i][0][0][j], f[i - 1][0][0][j] - g[i - 1][0][0][j] + g[i - 1][0][0][j] % 2 + g[i][0][0][j]);
f[0][i][j][0] = min(f[0][i][j][0], f[0][i][j - 1][0] - g[0][i][j - 1][0] + g[0][i][j - 1][0] % 4 + g[0][i][j][0]);
f[0][i][j][0] = min(f[0][i][j][0], f[0][i - 1][j][0] - g[0][i - 1][j][0] + g[0][i - 1][j][0] % 3 + g[0][i][j][0]);
f[0][i][0][j] = min(f[0][i][0][j], f[0][i][0][j - 1] - g[0][i][0][j - 1] + g[0][i][0][j - 1] % 5 + g[0][i][0][j]);
f[0][i][0][j] = min(f[0][i][0][j], f[0][i - 1][0][j] - g[0][i - 1][0][j] + g[0][i - 1][0][j] % 3 + g[0][i][0][j]);
f[0][0][i][j] = min(f[0][0][i][j], f[0][0][i][j - 1] - g[0][0][i][j - 1] + g[0][0][i][j - 1] % 5 + g[0][0][i][j]);
f[0][0][i][j] = min(f[0][0][i][j], f[0][0][i - 1][j] - g[0][0][i - 1][j] + g[0][0][i - 1][j] % 4 + g[0][0][i][j]);
}
}
for (register unsigned i(1); i <= m; ++i) {
if(!g[i][0][0][0]) break;
for (register unsigned j(1); j + i <= m; ++j) {
if(!g[i][j][0][0]) break;
for (register unsigned k(1); k + j + i <= m; ++k) {
if(!g[i][j][k][0]) break;
f[i][j][k][0] = min(f[i][j][k][0], f[i][j][k - 1][0] - g[i][j][k - 1][0] + g[i][j][k - 1][0] % 4 + g[i][j][k][0]);
f[i][j][k][0] = min(f[i][j][k][0], f[i][j - 1][k][0] - g[i][j - 1][k][0] + g[i][j - 1][k][0] % 3 + g[i][j][k][0]);
f[i][j][k][0] = min(f[i][j][k][0], f[i - 1][j][k][0] - g[i - 1][j][k][0] + g[i - 1][j][k][0] % 2 + g[i][j][k][0]);
f[i][j][0][k] = min(f[i][j][0][k], f[i][j][0][k - 1] - g[i][j][0][k - 1] + g[i][j][0][k - 1] % 5 + g[i][j][0][k]);
f[i][j][0][k] = min(f[i][j][0][k], f[i][j - 1][0][k] - g[i][j - 1][0][k] + g[i][j - 1][0][k] % 3 + g[i][j][0][k]);
f[i][j][0][k] = min(f[i][j][0][k], f[i - 1][j][0][k] - g[i - 1][j][0][k] + g[i - 1][j][0][k] % 2 + g[i][j][0][k]);
f[i][0][j][k] = min(f[i][0][j][k], f[i][0][j][k - 1] - g[i][0][j][k - 1] + g[i][0][j][k - 1] % 5 + g[i][0][j][k]);
f[i][0][j][k] = min(f[i][0][j][k], f[i][0][j - 1][k] - g[i][0][j - 1][k] + g[i][0][j - 1][k] % 4 + g[i][0][j][k]);
f[i][0][j][k] = min(f[i][0][j][k], f[i - 1][0][j][k] - g[i - 1][0][j][k] + g[i - 1][0][j][k] % 2 + g[i][0][j][k]);
f[0][i][j][k] = min(f[0][i][j][k], f[0][i][j][k - 1] - g[0][i][j][k - 1] + g[0][i][j][k - 1] % 5 + g[0][i][j][k]);
f[0][i][j][k] = min(f[0][i][j][k], f[0][i][j - 1][k] - g[0][i][j - 1][k] + g[0][i][j - 1][k] % 4 + g[0][i][j][k]);
f[0][i][j][k] = min(f[0][i][j][k], f[0][i - 1][j][k] - g[0][i - 1][j][k] + g[0][i - 1][j][k] % 3 + g[0][i][j][k]);
}
}
}
for (register unsigned i(1); i <= m; ++i) {
if(!g[i][0][0][0]) break;
for (register unsigned j(1); j + i <= m; ++j) {
if(!g[i][j][0][0]) break;
for (register unsigned k(1); k + j + i <= m; ++k) {
if(!g[i][j][k][0]) break;
for (register unsigned l(1); l + k + j + i <= m; ++l) {
if(!g[i][j][k][l]) break;
f[i][j][k][l] = min(f[i][j][k][l], f[i][j][k][l - 1] - g[i][j][k][l - 1] + g[i][j][k][l - 1] % 5 + g[i][j][k][l]);
f[i][j][k][l] = min(f[i][j][k][l], f[i][j][k - 1][l] - g[i][j][k - 1][l] + g[i][j][k - 1][l] % 4 + g[i][j][k][l]);
f[i][j][k][l] = min(f[i][j][k][l], f[i][j - 1][k][l] - g[i][j - 1][k][l] + g[i][j - 1][k][l] % 3 + g[i][j][k][l]);
f[i][j][k][l] = min(f[i][j][k][l], f[i - 1][j][k][l] - g[i - 1][j][k][l] + g[i - 1][j][k][l] % 2 + g[i][j][k][l]);
}
}
}
}
for (register unsigned i(0); i <= m; ++i) {
if(!g[i][0][0][0]) break;
for (register unsigned j(0); j + i <= m; ++j) {
if(!g[i][j][0][0]) break;
for (register unsigned k(0); k + j + i <= m; ++k) {
if(!g[i][j][k][0]) break;
for (register unsigned l(0); l + k + j + i <= m; ++l) {
if(!g[i][j][k][l]) break;
Ans = min(Ans, f[i][j][k][l]);
}
}
}
}
printf("%llu\n", Ans);
return Wild_Donkey;
}
```
但是因为不满冗长的预处理和奇妙的转移, 改变转移的顺序, 让代码变成这副模样, 成功将常数压缩 $6$ 倍.
```cpp
unsigned long long f[70][40][35][30], m, n, Ans(0x3f3f3f3f3f3f3f3f);
int main() {
n = RD(), m = RD() - 1;
memset(f, 0x3f, sizeof(f));
f[0][0][0][0] = n;
for (register unsigned long long i(0), Gi(n); (i <= m) && (Gi); ++i) {
for (register unsigned long long j(0), Gj(Gi); (j + i <= m) && (Gj); ++j) {
for (register unsigned long long k(0), Gk(Gj); (k + j + i <= m) && (Gk); ++k) {
for (register unsigned long long l(0), Gl(Gk); (l + k + j + i <= m) && (Gl); ++l) {
Ans = min(Ans, f[i][j][k][l]);
f[i + 1][j][k][l] = min(f[i + 1][j][k][l], f[i][j][k][l] - (Gl >> 1));
f[i][j + 1][k][l] = min(f[i][j + 1][k][l], f[i][j][k][l] - ((Gl / 3) << 1));
f[i][j][k + 1][l] = min(f[i][j][k + 1][l], f[i][j][k][l] - (Gl >> 2) * 3);
f[i][j][k][l + 1] = min(f[i][j][k][l + 1], f[i][j][k][l] - ((Gl / 5) << 2));
Gl /= 5;
}
Gk >>= 2;
}
Gj /= 3;
}
Gi >>= 1;
}
printf("%llu\n", Ans);
return Wild_Donkey;
}
```
### D
给 $n * n$ 的棋盘, 已经确定了若干位把 $[1, n^2]$ 每个数填入格子内, 要求一个数比它左边的数字大. 一些位置已经确定, 求一个字典序最小的方案 (从上到下, 从左到右计算). 无解输出 $-1$.
场上写的是 $O({n^2}^{n^2})$ 的巨大爆搜, 只有 $10'$.
半年过去了, 如今我想了一个类似于乱搞的算法, 美其名曰人工智能. 大体思路就是把棋盘看成是一堆区间, 每个区间内按约束填入对应数量的数字, 按顺序排好. 然后按从上到下, 从前往后的顺序, 每个区间依次填, 如果未分配数字不足以满足要求, 就从已经填入的区间厘米按借, 借来之后对那个借数字的区间递归进行同样的操作.
这个过程看似十分轻松写意, 但是本题对于这个算法最大的难点就是输出字典序最小的方案. 我们需要考虑所有的情况才能做出决定, 所以如果区间数量是 $m$, 猜测其复杂度是 $O(m!)$ 再乘上一个和 $n$ 有关的多项式复杂度. 最后因为算法仍有疏漏, 所以需要反复检查是否存在可交换的数字, 使得它们交换所属集合后能够减少字典序. 这一部分是 $O(n^5)$, 不足挂齿.
这个算法细节极多, 我花了一上午拿到 $85'$, 最后一个 Subtask TLE. 又花了一下午换了好几个写法, 从最朴素的写法到下面这份封装的指针写法 (万物皆可指针), 从原址移动到集合操作, 但是仅是速度提升了 $60\%$, 最后还是无法 AC. 但是正赛压轴题拿 $85'$ 已经很值了.
```cpp
#pragma GCC optimize("Ofast,no-stack-protector,unroll-loops,fast-math")
#pragma GCC target("sse,sse2,sse3,ssse3,sse4.1,sse4.2,avx,avx2,popcnt,tune=native")
unsigned a[10][10], m, n, Cnt(0);
unsigned B, C, D, t, Ans(0), Tmp(0), Time(0);
char Flg(0);
struct Ned;
struct Num {
Ned* Bel;
char Used, Ava, Pos;
}Nd[75];
struct Ned {
unsigned L, R, Len, Row, Col, Size, Tr, Last, Nb, Condi;
Num* Con[10];
inline void Copy() { for (unsigned i(0); i < Len; ++i) a[Row][Col + i] = Con[i] - Nd; }
inline void Erase(unsigned x) {
Con[x]->Used = 0, --Size;
for (unsigned i(x); i < Size; ++i) Con[i] = Con[i + 1], Con[i]->Pos = i;
}
inline void Insert(Num* x) {
(Con[Size] = x)->Used = 1, x->Pos = Size++;
for (unsigned i(Size - 1); i && (Con[i] < Con[i - 1]); --i) swap(Con[i], Con[i - 1]), Con[i]->Pos = i, x->Pos = i - 1;
}
inline void Print() {
printf("%u/%u: ", Size, Len);
for (unsigned i(0); i < Size; ++i) printf("%u ", Con[i] - Nd); putchar(0x0A);
}
inline unsigned Try() {//往 x 中填一个数字, 影响的最小的段的编号的最大值
for (unsigned i(L); i <= R; ++i) if (!Nd[i].Used) return Tr = Nb;
Last = 1, Condi = B;
unsigned Influ(0);
for (unsigned i(L); i <= R; ++i) if ((Nd[i].Used) && (!Nd[i].Ava) && (!(Nd[i].Bel->Last))) Influ = max(Influ, Nd[i].Bel->Try());
Last = 0;
return Tr = min(Nb, Influ);
}
inline unsigned Put() {
Tr = 0, Last = 1;
unsigned Ind(0), Best(0);
Ned* Nu(NULL);
for (unsigned i(L); (Best < Nb) && (i <= R); ++i) {
if (!Nd[i].Used) { Nu = Nd[i].Bel = this, Insert(Nd + i), Last = 0; return 1; }
if ((!Nd[i].Ava) && (!Nd[i].Bel->Last)) {
if (Nd[i].Bel->Try() >= Nb) {
Nd[i].Bel->Erase(Nd[i].Pos), Nu = Nd[i].Bel, Nd[i].Bel = this, Insert(Nd + i), Nu->Put(), Last = 0;
return 1;
}
if (Best <= Nd[i].Bel->Tr) Best = Nd[i].Bel->Tr, Nu = Nd[i].Bel, Ind = i;
}
}
if ((!Nu) || (!(Nu->Tr))) return 0;
Nu->Erase(Nd[Ind].Pos), Nd[Ind].Bel = this, Insert(Nd + Ind), Nu->Put(), Last = 0;
return 1;
}
}N[75];
int main() {
n = RD(), m = n * n;
for (unsigned i(1); i <= n; ++i) {
a[i][0] = 1;
for (unsigned j(1); j <= n; ++j) {
++(Nd[a[i][j] = RD()].Ava), ++(Nd[a[i][j]].Used);
if (a[i][j] != 0) {
for (unsigned k(1); k < j; ++k)
if (a[i][k] > a[i][j]) { printf("-1\n"); return 0; }
unsigned k(j - 1);
if ((!k) || a[i][k]) continue;
N[++Cnt].R = a[i][j] - 1;
N[Cnt].Row = i;
while (!a[i][k]) --k;
N[Cnt].Col = k + 1;
N[Cnt].L = a[i][k] + 1;
N[Cnt].Len = j - k - 1;
N[Cnt].Nb = Cnt;
if (k == 0) N[Cnt].L = 1;
}
}
if (!(a[i][n])) {
unsigned k(n);
N[++Cnt].R = n * n;
N[Cnt].Row = i;
while (!a[i][k]) --k;
N[Cnt].Col = k + 1;
N[Cnt].L = a[i][k] + 1;
N[Cnt].Len = n - k;
N[Cnt].Nb = Cnt;
if (k == 0) N[Cnt].L = 1;
}
}
for (unsigned i(m); i; --i) if (Nd[i].Ava > 1) { printf("-1\n");return 0; }
for (unsigned i(1); i <= Cnt; ++i) while (N[i].Size < N[i].Len) {
if (!N[i].Put()) { printf("-1\n"); return 0; }
}
for (unsigned i(2); i <= m; ++i) if (!Nd[i].Ava) {
for (unsigned j(1); j < i; ++j) if ((!Nd[j].Ava) && (Nd[i].Bel < Nd[j].Bel)) {
if ((Nd[i].Bel->L <= j) && (j <= Nd[i].Bel->R) && (Nd[j].Bel->L <= i) && (i <= Nd[j].Bel->R)) {
unsigned Fs(Nd[i].Pos), Sc(Nd[j].Pos);
Nd[i].Bel->Erase(Fs), Nd[j].Bel->Erase(Sc);
swap(Nd[i].Bel, Nd[j].Bel);
Nd[i].Bel->Insert(Nd + i);
Nd[j].Bel->Insert(Nd + j);
}
}
}
for (unsigned i(1); i <= Cnt; ++i) N[i].Copy();
for (unsigned i(1); i <= n; ++i) {
for (unsigned j(1); j <= n; ++j) printf("%u ", a[i][j]); putchar('\n');
}
return Wild_Donkey;
}
```
但是正如罗曼罗兰所说: 世界上只有一种真正的英雄主义, 那就是在认识生活的真相后依然热爱生活. 今天我也要说: OI 中只有一种真正的英雄主义, 那就是在认识自己的算法无法通过题目后依然用标算把这个题 A 掉. 我最终还是向标算敞开了怀抱.
标算的思路是我上面算法的推广和改进. 仍然是强行把数字分配到集合里面, 我们使用网络流解决此题, 源点向每个区间连容量为区间长度的边, 每个区间向自己范围内的数字连容量为 $1$ 的边, 每个数字都向汇点连一条容量为 $1$ 的边. 最大流如果是待分配的点数, 说明当前局面有解. 因为这个建模和二分图最大匹配极为相似, 两边点数都是 $O(n^2)$, 而边数为 $O(n^4)$. 所以我们姑且认为 Dinic 一次的效率是 $O(n^5)$.
为了求字典序最小的方案, 我们从高位到低位考虑, 枚举 $O(n^2)$ 个数字填哪一个, 每次判断可行性, 只要可行就继续填, 这样一个位置的确定最多需要 $O(n^7)$ 的时间. 对每个位置做同样的操作, 共需要 $O(n^9)$. 而且本题每个位置可填的数字都有 $O(n^2)$ 个是几乎不可能的, 而每次都枚举到最后一个数字才可行的情况也是几乎不可能的. 因此 $O(n^9)$ 只是一个比较宽的上界, 就算顶满也不过 $10^8$.
最后还是吹一波指针, 真的可以用赏心悦目来形容了.
```cpp
unsigned a[10][10], m, n, Cnt(0);
unsigned B, C, D, t, Ans(0), Tmp(0);
char Flg(0), Ava[75];
struct Node;
struct Edge {
Node* To;
unsigned Cap, Inv;
};
struct Node {
vector <Edge> E;
unsigned Dep;
}N[105], * Que[105], ** Hd(Que), ** Tl(Que);
struct Range {
unsigned L, R, Len, Row, Col;
vector <unsigned>Con;
inline void Copy() {
sort(Con.begin(), Con.end());
for (unsigned i(0); i < Len; ++i) a[Row][Col + i] = Con[i];
}
inline void Print() {
printf("%u/%u: ", Con.size(), Len);
for (unsigned i(0); i < Con.size(); ++i) printf("%u ", Con[i]); putchar(0x0A);
}
}R[75];
inline char BFS() {
Hd = Tl = Que, (*(++Tl) = N)->Dep = 0;
for (Node* i(N + Cnt + m + 1); i > N; --i) i->Dep = 0x3f3f3f3f;
while (Hd != Tl) {
Node* Cur(*(++Hd));
for (auto i : Cur->E) if ((i.Cap) && (i.To->Dep >= 0x3f3f3f3f)) i.To->Dep = Cur->Dep + 1, * (++Tl) = i.To;
}
return N[Cnt + m + 1].Dep < 0x3f3f3f3f;
}
inline unsigned DFS(Node* x, unsigned Come) {
if (x == N + Cnt + m + 1) return Come;
unsigned Gone(0);
for (auto i : x->E) if ((i.Cap) && (i.To->Dep > x->Dep)) {
unsigned Push(min(i.Cap, Come));
Push = DFS(i.To, Push);
i.To->E[i.Inv].Cap += Push;
x->E[i.To->E[i.Inv].Inv].Cap -= Push;
Come -= Push, Gone += Push;
}
return Gone;
}
inline char Judge(unsigned x, unsigned y) {
unsigned Flow(0), Total(0);
for (unsigned i(1); i <= Cnt; ++i) Total += (N->E[i - 1].Cap = R[i].Len - R[i].Con.size()), N[i].E[0].Cap = 0;
for (unsigned i(1); i <= m; ++i) N[Cnt + i].E[0].Cap = Ava[i] ? 0 : 1, N[Cnt + m + 1].E[i - 1].Cap = 0;
for (unsigned i(1); i <= Cnt; ++i) for (unsigned j(R[i].L); j <= R[i].R; ++j)
N[i].E[j - R[i].L + 1].Cap = 1, N[Cnt + j].E[N[i].E[j - R[i].L + 1].Inv].Cap = 0;
--(N->E[x - 1].Cap), --(N[Cnt + y].E[0].Cap), --Total;
while (BFS()) Flow += DFS(N, 0x3f3f3f3f);
return Flow >= Total;
}
int main() {
n = RD(), m = n * n;
for (unsigned i(1); i <= n; ++i) {
a[i][0] = 1;
for (unsigned j(1); j <= n; ++j) {
++Ava[a[i][j] = RD()];
if (a[i][j] != 0) {
for (unsigned k(1); k < j; ++k)
if (a[i][k] > a[i][j]) { printf("-1\n"); return 0; }
unsigned k(j - 1);
if ((!k) || a[i][k]) continue;
R[++Cnt].R = a[i][j] - 1;
R[Cnt].Row = i;
while (!a[i][k]) --k;
R[Cnt].Col = k + 1;
R[Cnt].L = a[i][k] + 1;
R[Cnt].Len = j - k - 1;
if (k == 0) R[Cnt].L = 1;
}
}
if (!(a[i][n])) {
unsigned k(n);
R[++Cnt].R = n * n;
R[Cnt].Row = i;
while (!a[i][k]) --k;
R[Cnt].Col = k + 1;
R[Cnt].L = a[i][k] + 1;
R[Cnt].Len = n - k;
if (k == 0) R[Cnt].L = 1;
}
}
for (unsigned i(m); i; --i) if (Ava[i] > 1) { printf("-1\n");return 0; }
for (unsigned i(1); i <= Cnt; ++i) {
N[0].E.push_back((Edge) { N + i, 0, N[i].E.size() });
N[i].E.push_back((Edge) { N, 0, N->E.size() - 1 });
}
for (unsigned i(1); i <= m; ++i) {
N[Cnt + i].E.push_back((Edge) { N + Cnt + m + 1, 0, N[Cnt + m + 1].E.size() });
N[Cnt + m + 1].E.push_back((Edge) { N + Cnt + i, 0, N[Cnt + i].E.size() - 1 });
}
for (unsigned i(1); i <= Cnt; ++i) for (unsigned j(R[i].L); j <= R[i].R; ++j) {
N[i].E.push_back((Edge) { N + Cnt + j, 0, N[Cnt + j].E.size() });
N[Cnt + j].E.push_back((Edge) { N + i, 0, N[i].E.size() - 1 });
}
for (unsigned i(1); i <= Cnt; ++i) while (R[i].Con.size() < R[i].Len) {
Flg = 0;
for (unsigned j(R[i].L); j <= R[i].R; ++j) if (!Ava[j]) { if (Judge(i, j)) { R[i].Con.push_back(j), Ava[j] = 1, Flg = 1; break; } }
if (!Flg) { printf("-1\n");return 0; }
}
for (unsigned i(1); i <= Cnt; ++i) R[i].Copy();
for (unsigned i(1); i <= n; ++i) {
for (unsigned j(1); j <= n; ++j) printf("%u ", a[i][j]); putchar('\n');
}
return Wild_Donkey;
}
```
## Day28: 基础数论
### 欧拉函数
设 $p_i$ 为第 $i$ 个质数, 则欧拉函数可以表示为:
$$
\phi(x) = \frac{x}{\displaystyle{\prod_{p_i | x}(p_i - 1)}}
$$
$\phi$ 是积性函数, 因为对于互质的 $x$ 和 $y$, 它们没有公共质因数, 所以有:
$$
\begin{aligned}
&\phi(x)\phi(y)\\
= &\frac{x}{\displaystyle{\prod_{p_i | x}(p_i - 1)}} \times \frac{y}{\displaystyle{\prod_{p_i | y}(p_i - 1)}}\\
= &\frac{xy}{\displaystyle{\prod_{p_i | x \lor p_i | y}(p_i - 1)}}\\
= &\frac{xy}{\displaystyle{\prod_{p_i | xy}(p_i - 1)}}\\
= &\phi(xy)
\end{aligned}
$$
### 欧拉定理
对于互质的 $a$, $p$, 有:
$$
a^{\phi(p)} \equiv 1 \pmod p
$$
所以就有:
$$
a^{b} \equiv a^{b \% \phi(p)} \pmod p
$$
### 扩展欧拉定理
对于不保证 $a$, $p$ 互质的情况:
$$
\begin{aligned}
a^b &\equiv a^{b \% \phi(p)} &\pmod p &(gcd_{a, p} = 1)\\
a^b &\equiv a^b &\pmod p &(gcd_{a, p} \neq 1, b < \phi(p))\\
a^b &\equiv a^{b \% \phi(p) + \phi(p)} &\pmod p&(gcd_{a, p} \neq 1, b \geq \phi(p))
\end{aligned}
$$
### 埃氏筛
扫描正整数, 一个数没有被筛过, 则它是质数, 对于每一个质数, 筛出它的所有倍数. 时间复杂度 $O(n\log(\log n))$. 可以用来求积性函数.
### 欧拉筛
仍然扫描, 但是一个质数 $p$ 筛别的数的时候, 如果 $p$ 不是待筛的数的最大质因子, 则停止. 这样可以保证一个数仅被筛掉一次, 也就是被它的最大质因数筛掉.
为了在 $p$ 不是最大质因数的时候跳出, 当和 $p$ 相乘的因数能被 $p$ 整除的时候跳出即可, 复杂度是线性. 可以用来求积性函数.
### 求 $\binom {n}{m}$ 中 $p$ 的幂次
分别求 $n!$, $m!$ 和 $(n - m)!$ 中 $p$ 的幂次, 然后做减法即可.
如何求阶乘的幂次, 用 $n$ 不断除以 $p$, 则 $n!$ 中 $p$ 的幂次可以表示为:
$$
\sum_{i \geq 1} \lfloor \frac {n}{p^i} \rfloor
$$
所以答案就是
$$
\sum_{i \geq 1} (\lfloor \frac {n}{p^i} \rfloor - \lfloor \frac {m}{p^i} \rfloor - \lfloor \frac {n - m}{p^i} \rfloor)
$$
尝试发现 $p$ 的幂次的新意义.
$$
\begin{aligned}
m &= a_1p^i + r_1~(r_1 < p^i)\\
n - m &= a_2p^i + r_2~(r_2 < p^i)\\
n &= (a_1 + a_2)p^i + r_1 + r_2\\
n &= a_3p^i + r_3\\
r_3 &= (r_1 + r_2) \% p^i\\
a_3 &= a_1 + a_2 + \lfloor \frac {r_1 + r_2}{p^i} \rfloor
\end{aligned}
$$
发现这就是 $m$ 和 $n - m$ 在 $p$ 进制加法中的进位次数.
### Baby-Step Giant-Step
求满足 $a^x \equiv b \pmod p$ 的最小自然数 $x$, 满足 $a$ 和 $p$ 互质.
首先将 $b$ 变成 $b \% p$.
因为 $a^x \equiv a^{x \% \phi(p)}$, 所以 $x < \phi (p)$.
设 $Sq = \lceil \sqrt \phi (p) \rceil$, 将 $x$ 分解成 $kSq + r$, 因为 $x < p$, 所以 $k, r \leq Sq$.
原来的式子变成:
$$
\begin{aligned}
a^x &\equiv b \pmod p\\
a^{kSq + r} &\equiv b \pmod p\\
a^{kSq} &\equiv bInv_{a^{r}} \pmod p
\end{aligned}
$$
预处理出对于所有 $r \leq Sq$ 的 $BInv_{a^{r}}$, 存入 `map`, 然后枚举 $k$, 在 `map` 中查询 $a^{kSq}$, 如果存在, 那么就找到一个特解 $x$. 复杂度 $O(\sqrt p \log \sqrt p)$. 使用 `unordered_map` 还能做到 $O(\sqrt p)$.
接下来将解最小化. 因为 $a$, $p$ 互质时, $a^x \% p$ 的结果随着 $x$ 的增加以 $\phi (p)$ 为周期循环, 因此只要将 $x$ 对 $\phi(p)$ 取模即可. 而且因为我们只能求出 $[0, Sq^2]$ 之间的答案, 所以大部分情况下不取模也是对的, 只是因为向上取整导致我们可能会找到大于等于 $\phi(p)$ 的结果.
这就是大步小步 (Baby-Step Giant-Step, BSGS) 算法.
### [TJOI2007](https://www.luogu.com.cn/problem/P3846)
给定质数 $p$, 求出对于给定的 $a$, $b$, 最小的 $x$, 使得 $a^x \equiv b \pmod p$. BSGS 模板题.
```cpp
unsigned Inv[100005];
unsigned long long a, b, p, Tmp;
unsigned n, A, B, C, D, t;
unsigned Cnt(0), Ans(0);
unordered_map<unsigned, unsigned> S;
unsigned long long Pow(unsigned long long x, unsigned y) {
unsigned long long Rt(1);
while (y) { if (y & 1) Rt = Rt * x % p; x = x * x % p, y >>= 1; }
return Rt;
}
signed main() {
p = RD(), a = RD(), b = RD(), n = sqrt(p - 1) + 1, Inv[n] = Pow(Tmp = Pow(a, n), p - 2) * b % p;
for (unsigned i(n - 1); ~i; --i) S[Inv[i] = Inv[i + 1] * a % p] = i;
for (unsigned i(0), j(1); i < n; ++i, j = j * Tmp % p)
if (S.find(j) != S.end()) { printf("%u\n", (i * n + S[j]) % (p - 1));return 0; }
printf("no solution\n");
return Wild_Donkey;
}
```
### Extended Baby-Step Giant-Step
然后考虑 $a$, $p$ 不互质的情况, 因为这时可能不存在 $Inv_{a^r}$. 记 $\gcd(a, p) = g$.
首先判有解, 有解当且仅当 $g|b$. 将方程转化为 $\frac {a}{g} a^{x - 1} \equiv \frac {b}{g} \pmod {\frac {p}{g}}
如果这时 a 和 \frac{p}{g} 仍不互质, 仍然同时除以 gcd. 直到 a 和 p 互质位置这时方程会变成:
\begin{aligned}
\frac {a^{x}}{\displaystyle{\prod_{i}g_i}} &\equiv \frac {b}{\displaystyle{\prod_{i}g_i}} \pmod {\frac {p}{\displaystyle{\prod_{i}g_i}}}\\
\frac {a^{k}}{\displaystyle{\prod_{i}g_i}} a^{x - k} &\equiv \frac {b}{\displaystyle{\prod_{i}g_i}} \pmod {\frac {p}{\displaystyle{\prod_{i}g_i}}}\\
a^{x - k} &\equiv \frac {b}{\displaystyle{\prod_{i}g_i}} Inv_{\frac {a^{k}}{\displaystyle{\prod_{i}g_i}}} \pmod {\frac {p}{\displaystyle{\prod_{i}g_i}}}\\
a^{x - k} &\equiv \frac {b\displaystyle{\prod_{i}g_i}}{a^{k}\displaystyle{\prod_{i}g_i}} \pmod {\frac {p}{\displaystyle{\prod_{i}g_i}}}\\
a^{x - k} &\equiv \frac {b}{a^k} \pmod {\frac {p}{\displaystyle{\prod_{i}g_i}}}\\
a^{x - k} &\equiv bInv_{a^k} \pmod {\frac {p}{\displaystyle{\prod_{i}g_i}}}\\
\end{aligned}
这时 a 和 \frac {p}{\displaystyle{\prod_{i}g_i}} 互质, 则将 bInv_{a^k} 作为新的 b, \frac {p}{\displaystyle{\prod_{i}g_i}} 作为新的 p, 做一次正常 BSGS 即可. 答案就是正常 BSGS 答案 + k 即可. 这便是扩展大步小步 (Extended Baby-Step Giant-Step, ExBSGS) 算法.
P4195
给三个自然数数 a, b, p, 求最小的自然数 x 满足 a^x \equiv b \pmod p, 无解输出 No Solution. ExBSGS 模板题.
unsigned long long a, b, p, B, P, Ph, Inv, Tmp;
unsigned n, C, D, t, A;
unsigned Cnt(0), Ans(0);
char Flg(0);
inline char Clr() {
a = RD(), P = p = RD(), b = RD(), C = Flg = 0;
if (!p) return 1;
b %= p, B = b, A = 1;
return 0;
}
inline unsigned long long Pow(unsigned long long x, unsigned y) {
unsigned long long Rt(1);
while (y) { if (y & 1) Rt = Rt * x % P; x = x * x % P, y >>= 1; }
return Rt;
}
inline unsigned Phi(unsigned x) {
unsigned Rt(x), Li(sqrt(x) + 1);
for (unsigned i(2); i <= Li; ++i) if (!(x % i)) {
Rt /= i, Rt *= (i - 1);
while (!(x % i)) x /= i;
}
if (x > 1) Rt /= x, Rt *= (x - 1);
return Ph = Rt;
}
inline unsigned GCD(unsigned long long x, unsigned long long y) {
unsigned SwT;
while (y) SwT = x, x = y, y = SwT % y;
return D = x;
}
inline void BSGS() {
unordered_map<unsigned, unsigned> S;
Inv = B * Pow(Tmp = Pow(a, n), Ph - 1) % P;
for (unsigned i(n - 1); ~i; --i) S[Inv = Inv * a % P] = i;
for (unsigned i(0), j(1); i < n; ++i, j = j * Tmp % P)
if (S.find(j) != S.end()) { printf("%llu\n", ((i * n + S[j]) % Ph) + C); return; }
printf("No Solution\n"); return;
}
signed main() {
for (;;) {
if (Clr()) return 0;
if (b == 1) { printf("0\n");continue; }
if (!a) { printf(b ? "No Solution\n" : "1"); continue; }
while (GCD(a, P) > 1) if (!(b % D)) b /= D, P /= D, ++C, A = A * (a / D) % P;
else { Flg = 1, printf((b ^ A) ? "No Solution\n" : "%u\n", C); break; }
if (Flg) continue;
n = sqrt(Phi(P)) + 1;
B = Pow(Pow(a, C), Ph - 1) * B % P;
BSGS();
}
return Wild_Donkey;
}
莫比乌斯函数
设 x = \prod_i p_i^{a_i}.
\mu(x) =
\begin{cases}
-1^{\sum a_i}, & (\forall a_i \leq 1)\\
0, & (\exists a_i \geq 2)
\end{cases}
狄利克雷卷积
f(i) = \sum_{j|i} a_jb_{\frac ij}
假设将每一项都是 1 的序列记为 1, 有结论 1 * \mu = \epsilon. \epsilon 是狄利克雷卷积的单位元. 什么序列卷 \epsilon 都是它本身. \epsilon 的第一项是 1, 其它项都是 0. \epsilon(1) = 1, \epsilon (i > 1) = 0.
狄利克雷卷积满足乘法交换律, 结合律, 分配律.
只要 f(1) != 0, 则 f(x) 的狄利克雷卷积逆元 g(x), 使得 f * g = \epsilon. 尝试构造之:
\begin{aligned}
\epsilon &= g * f\\
\epsilon(x) &= \sum_{d|x} f(d)g(\frac xd)\\
\epsilon(x) &= \sum_{d|x,d \neq 1} f(d)g(\frac xd) + f(1)g(x)\\
f(1)g(x) &= \epsilon(x) - \sum_{d|x,d \neq 1} f(d)g(\frac xd)\\
g(x) &= \frac{\epsilon(x) - \displaystyle{\sum_{d|x, d \neq 1} f(d)g(\frac xd)}}{f(1)}
\end{aligned}
莫比乌斯反演
其原理是:
\sum_{i | n} \mu(i) = [n = 1]
对于 f, g, 如果有:
f_i = \sum_{j | i} g_j
则有:
\begin{aligned}
g_i &= \sum_{j | i} g_j [\frac ij = 1]\\
g_i &= \sum_{j | i} g_j \sum_{k | \frac ij} \mu(k)\\
g_i &= \sum_{j | i} \sum_{k | \frac ij} f_j \mu(k)\\
g_i &= \sum_{jk | i} g_j \mu(k)\\
g_i &= \sum_{j | i} \sum_{k | \frac ij} g_k \mu(j)\\
g_i &= \sum_{j | i} \mu(j) \sum_{k | \frac ij} g_k\\
g_i &= \sum_{j | i} \mu(j) f_{\frac ij}\\
\end{aligned}
这便是莫比乌斯反演公式.
P1516
两个青蛙, 初始分别在长度为 p 的环上的 a, b 两点, 每单位时间分别往正方向走 n, m 单位长度, 求是否能相遇, 如果能, 求最小相遇时间, 否则输出 Impossible.
转化为对 n, m, 求满足 a + xn \equiv b + xm \pmod {p} 的最小的 x.
\begin{aligned}
a + xn &\equiv b + xm \pmod {p}\\
x(n - m) &\equiv b - a \pmod {p}\\
x(n - m) &= b - a + kp\\
x(n - m) - k p &= b - a
\end{aligned}
用 Exgcd 求出 x 即可.
long long Ks, Wh, a, b, c, d;
unsigned A, B, C, D, t;
unsigned Cnt(0), Ans(0), Tmp(0);
long long Gcd(long long x, long long y) {
long long STm;
while (y) { STm = x, x = y, y = STm % y; }
return x;
}
inline void Exgcd(long long x, long long y) {
long long STm, Stack[105];
unsigned STop(0);
while (y) Stack[++STop] = x / y, STm = x, x = y, y = STm % y;
Ks = x, Wh = 0;
for (;STop;--STop) STm = Wh, Wh = Ks - Wh * Stack[STop], Ks = STm;
}
signed main() {
c = RD(), c = RD() - c, a = RD(), a -= RD(), b = RD(), b = -b;
d = Gcd((a > 0) ? a : -a, (b > 0) ? b : -b); if (d < 0) d = -d;
if (c % d) { printf("Impossible\n"); return 0; }
a /= d, b /= d, c /= d;
Exgcd(a, b);
if (b < 0) b = -b;
Ks *= c, Ks %= b, Ks += b;
if (Ks >= b) Ks -= b;
printf("%lld\n", Ks);
return Wild_Donkey;
}
NOI2010
求:
\begin{aligned}
&\sum_{i = 1}^n \sum_{j = 1}^m (2gcd(i, j) - 1)\\
= &2 (\sum_{i = 1}^n \sum_{j = 1}^m gcd(i, j)) - mn\\
\end{aligned}
转化为求 gcd 的总和, 然后转化为枚举 gcd:
\begin{aligned}
&\sum_{i = 1}^n \sum_{j = 1}^m gcd(i, j)\\
= &\sum_{d = 1}^n \sum_{i = 1}^n \sum_{j = 1}^m [\gcd(i, j) = d]\\
=&\sum_{d = 1}^n d\sum_{i = 1}^{\lfloor \frac{n}{d} \rfloor}\sum_{j = 1}^{\lfloor \frac{m}{d} \rfloor}[gcd(i, j) = 1]\\
\end{aligned}
变成了求一定范围内 i, j 互质的数量. 我们先来考虑 n = m 的做法, 说到互质的数量, 就不得不提到欧拉函数 \phi, 因为 \phi(x) 表示小于等于 x 的和 x 互质的正整数数量. 我们按 i 和 j 的大小关系, 把有序对 (i, j) 分为三类, 由于 i < j 和 j > i 的情况是完全对称的, 所以只求其中一种情况然后乘 2 即可. 对于 i = j 的情况, 每个 d 在前面算出的结果 -1 即可. 为了求 \lfloor \frac{n}{d} \rfloor 以内满足 i > j 的 i 和 j 的数量, 有 \sum_{i = 1}^{\phi(\lfloor \frac{n}{d} \rfloor)} \phi(i) - 1 对. 其中减去的 1 是因为 \phi(1) = 1, 而 1 和 1 互质但是不满足 1 > 1, 所以还要加 1.
前缀和可以用欧拉筛预处理, 所以复杂度线性, 需要求:
2(\sum_{d = 1}^n (2\sum_{i = 1}^{\phi(\lfloor \frac{n}{d} \rfloor)} \phi(i)) - 1) - mn
好的这样一顿操作下来就可以拿到 10' 了:
unsigned long long Sum[100005], Ans(0);
unsigned Prime[100005], m, n;
unsigned A, B, C, D, t;
unsigned Cnt(0), Tmp(0);
bitset<100005> Isnt;
signed main() {
n = RD(), m = RD(), Sum[1] = 1;
if (n < m) swap(n, m);
for (unsigned i(2); i <= n; ++i) {
if (!Isnt[i]) Prime[++Cnt] = i, Sum[i] = i - 1;
for (unsigned j(1); (j <= Cnt) && (Prime[j] * i <= n); ++j) {
unsigned Des(Prime[j] * i);
Isnt[Des] = 1, Sum[Des] = Sum[Prime[j]] * Sum[i];
if (!(i % Prime[j])) { Sum[Des] /= Prime[j] - 1, Sum[Des] *= Prime[j]; break; }
}
}
for (unsigned i(1); i <= n; ++i) Sum[i] += Sum[i - 1];
for (unsigned i(1); i <= m; ++i) Ans += (Sum[m / i] + Sum[n / i] - 1) * i;
printf("%llu\n", (Ans << 1) - ((unsigned long long)n * m));
return Wild_Donkey;
}
考虑莫比乌斯反演.
\begin{aligned}
&\sum_{d = 1}^n d\sum_{i = 1}^{\lfloor \frac{n}{d} \rfloor}\sum_{j = 1}^{\lfloor \frac{m}{d} \rfloor}[gcd(i, j) = 1]\\
=&\sum_{d = 1}^n d\sum_{i = 1}^{\lfloor \frac{n}{d} \rfloor}\sum_{j = 1}^{\lfloor \frac{m}{d} \rfloor} \sum_{k | gcd(i, j)} \mu(k)\\
=&\sum_{d = 1}^n d\sum_{i = 1}^{\lfloor \frac{n}{d} \rfloor}\sum_{j = 1}^{\lfloor \frac{m}{d} \rfloor} \sum_{k | i, k | j} \mu(k)\\
=&\sum_{d = 1}^n d\sum_{k = 1}^{\lfloor \frac nd \rfloor} \mu(k) \sum_{i = 1}^{\lfloor \frac{n}{dk} \rfloor}\sum_{j = 1}^{\lfloor \frac{m}{dk} \rfloor} 1\\
=&\sum_{d = 1}^n d\sum_{k = 1}^{\lfloor \frac nd \rfloor} \mu(k) \lfloor \frac{n}{dk} \rfloor \lfloor \frac{m}{dk} \rfloor\\
\end{aligned}
这个式子直接计算的复杂度相当于是调和级数求和, 是 O(n \ln n).
long long Mu[100005], Ans(0), Tmp(0);
unsigned Prime[100005], m, n;
unsigned A, B, C, D, t;
unsigned Cnt(0);
bitset<100005> Isnt;
signed main() {
n = RD(), m = RD(), Mu[1] = 1;
if (n < m) swap(n, m);
for (unsigned i(2); i <= n; ++i) {
if (!Isnt[i]) Prime[++Cnt] = i, Mu[i] = -1;
for (unsigned j(1); (j <= Cnt) && (Prime[j] * i <= n); ++j) {
unsigned Des(Prime[j] * i);
Isnt[Des] = 1, Mu[Des] = Mu[Prime[j]] * Mu[i];
if (!(i % Prime[j])) { Mu[Des] = 0; break; }
}
}
for (unsigned i(1); i <= m; ++i, Tmp = 0) {
for (unsigned j(m / i), Nd(n / i), Md(m / i); j; --j) Tmp += Mu[j] * (Nd / j) * (Md / j);
Ans += i * Tmp;
}
printf("%llu\n", (Ans << 1) - ((unsigned long long)n * m));
return Wild_Donkey;
}
POI2007
给 n 个询问, 每个询问给出 a, b, d, 求满足 x \leq a, y \leq b, gcd(x, y) = d 的正整数有序对 (x, y) 的数量.
和上一题一样的转化过程:
\begin{aligned}
&\sum_{i = 1}^a \sum_{j = 1}^b [gcd(i, j) = d]\\
=&\sum_{i = 1}^{\lfloor \frac ad \rfloor} \sum_{j = 1}^{\lfloor \frac bd \rfloor} [gcd(i, j) = 1]\\
=&\sum_{i = 1}^{\lfloor \frac ad \rfloor} \sum_{j = 1}^{\lfloor \frac bd \rfloor} \sum_{k | i, k | j} \mu(k)\\
=&\sum_{k = 1}^{\lfloor \frac ad \rfloor} \mu(k)\lfloor \frac a{dk} \rfloor \lfloor \frac b{dk} \rfloor\\
\end{aligned}
如果直接算这个式子的话, O(n\min(a, b)) 很明显是要超时的, 但是明显这个可以通过预处理 \mu 的前缀和加整除分块优化到 O(\max(\min(a, b)) + n\sum\sqrt{\min(a, b)}). (远古稚嫩代码警告)
int n, m, N, Pri[50004]/*存所有质数*/, t/*存n,m*/, d;
long long ans/*第0行和第0列的两个点提前算上*/, Mu[50004]/*一开始是μ(x), 后成前缀和*/;
bool Isntpri[50004]/*欧拉筛标记*/;
inline void Read(int & x) {//读入模块
int f = 1;
char c = getchar();
x = 0;
while (c < '0' || c>'9') {
if (c == '-')f = -1;
c = getchar();
}
while (c >= '0' && c <= '9') {
x = (x << 3) + (x << 1) + c - '0';
c = getchar();
}
x *= f;
}
inline void Prime(int x) {//欧拉筛求Mu(x)
Mu[1] = 1;//递推边界
for (register int i = 2; i <= x; i++) {//从2开始递推
if (!Isntpri[i]) {//没有被筛到过, i是质数
Pri[++Pri[0]] = i;//记录到Pri里
Mu[i] = -1;//质数只有一个质因数(它本身), 所以Mu(i)等于-1
}
for (register int j = 1; (j <= Pri[0]) && (i * Pri[j] <= x); j++) {//不管i是不是质数, 都要乘部分已知质数(积一定小于等于i^2)
Isntpri[i * Pri[j]] = 1;//筛掉积, 积一定是合数
if (i % Pri[j] == 0) {//当前质数是i的质因数时, 设i=n*Pri[j]=m*Pri[j+1], 则合数i*Pri[j]已经被筛掉了(先筛后Break), 而Pri[j+1]*i一定会被Pri[j+1]^2筛掉(或者是被Pri[j+k]筛掉)
break;
}//这样便可以不重不漏O(n)筛出所有质数
Mu[i * Pri[j]] = -Mu[i];//别忘了处理Mu(x)(积性函数只要用一对因数的函数值相乘就好)
}
}
}
int main() {
Prime(50004);//欧拉筛, 求出莫比乌斯函数Mu(x)
for (register int i = 1; i <= 50004; i++) {//这时的Mu(x)已经不是莫比乌斯函数了, 而是莫比乌斯函数的前缀和
Mu[i] = (Mu[i] + Mu[i - 1]) % 19268017;
}
Read(N);
for (int inn = 1; inn <= N; inn++) {
Read(n);
Read(m);
Read(d);//输入
n /= d;
m /= d;
if (n > m) {//先用T,t表示n,m中较大的和较小的
t = m;
}
else {
t = n;
}
ans = 0;
for (register int l = 1, r; l <= t; l = r + 1) {//这时开始进行分段优化
if (n / (n / l) < m / (m / l)) {//之前说的从区间任意点求区间终点的方法, 选择较小的
r = n / (n / l);
}
else {
r = m / (m / l);
}
ans += (Mu[r] - Mu[l - 1]) * (n / l) * (m / l);//这里的前缀和相减求出来的就是Mu(x)函数值从l到r的总和, 乘上这个暂时不变的积
}
printf("%lld\n", ans);//直接输出答案
}
return 0;
}
P1829
给 n, m, 求 \displaystyle{\sum_{i = 1}^{n} \sum_{j = 1}^{m} lcm(i, j)}, 结果对 20101009 取模. (20101009 是质数).
\begin{aligned}
&\sum_{i = 1}^n \sum_{j = 1}^m lcm(i, j)\\
=&\sum_{i = 1}^n \sum_{j = 1}^m \frac {ij}{gcd(i, j)}\\
=&\sum_{d = 1}^n \frac 1d \sum_{i = 1}^{\lfloor \frac nd \rfloor} \sum_{j = 1}^{\lfloor \frac md \rfloor} ijd^2 [gcd(i, j) = 1]\\
=&\sum_{d = 1}^n d \sum_{i = 1}^{\lfloor \frac nd \rfloor} \sum_{j = 1}^{\lfloor \frac md \rfloor} ij \sum_{k | i, k | j} \mu(k)\\
=&\sum_{d = 1}^n d \sum_{k = 1}^{\lfloor \frac nd \rfloor} \mu(k) \sum_{i = 1}^{\lfloor \frac n{dk} \rfloor} \sum_{j = 1}^{\lfloor \frac m{dk} \rfloor} ijk^2\\
=&\sum_{d = 1}^n d \sum_{k = 1}^{\lfloor \frac nd \rfloor} \mu(k)k^2 \sum_{i = 1}^{\lfloor \frac n{dk} \rfloor} i\sum_{j = 1}^{\lfloor \frac m{dk} \rfloor} j\\
=&\sum_{d = 1}^n d \sum_{k = 1}^{\lfloor \frac nd \rfloor} \mu(k)k^2 \frac {(1 + \lfloor \frac m{dk} \rfloor)\lfloor \frac m{dk} \rfloor}2 \sum_{i = 1}^{\lfloor \frac n{dk} \rfloor} i\\
=&\sum_{d = 1}^n d \sum_{k = 1}^{\lfloor \frac nd \rfloor} \frac {\mu(k)k^2(1 + \lfloor \frac n{dk} \rfloor)\lfloor \frac n{dk} \rfloor(1 + \lfloor \frac m{dk} \rfloor)\lfloor \frac m{dk} \rfloor}4\\
\end{aligned}
这样算也是 O(n \ln n) 的, n \leq 10^7 不太行, 实测无论是否开 -O2 都是 75'.
const long long Mod(20101009), Inv(15075757);
long long Ans(0), Tmp(0);
int Mu[10000005];
unsigned m, n;
unsigned A, B, C, D, t;
unsigned Prime[1000005], Cnt(0);
bitset<10000005> No;
signed main() {
n = RD(), m = RD(), Mu[1] = 1; if (n > m) swap(n, m);
for (unsigned i(2); i <= m; ++i) {
if (!No[i]) Prime[++Cnt] = i, Mu[i] = -1;
for (unsigned j(1), Des(i << 1); (j <= Cnt) && (Des <= m); ++j, Des = Prime[j] * i) {
No[Des] = 1, Mu[Des] = Mu[i] * Mu[Prime[j]];
if (!(i % Prime[j])) { Mu[Des] = 0; break; }
}
}
for (unsigned i(1); i <= n; ++i, Tmp = 0) {
long long Nd(n / i), Md(m / i);
for (long long j(Nd), Sq(Nd* Nd% Mod), Nk, Mk; j; --j, Sq = j * j % Mod)
Nk = Nd / j, Mk = Md / j, Tmp = (Tmp + (((((Mu[j] * Sq % Mod) * (Nk + 1) % Mod) * (Mk + 1) % Mod) * Nk % Mod) * Mk % Mod) * Inv) % Mod;
Ans = (Ans + i * Tmp) % Mod;
}
printf("%lld\n", Ans);
return Wild_Donkey;
}
仍然是前缀和加整除分块优化, 把每次枚举第二维的复杂度扣上个根号, 具体的复杂度我也不会算, 反正就是过了.
const long long Mod(20101009), Inv(15075757);
long long Mu[10000005], Ans(0), Tmp(0);
unsigned m, n;
unsigned A, B, C, D, t;
unsigned Prime[1000005], Cnt(0);
bitset<10000005> No;
signed main() {
n = RD(), m = RD(), Mu[1] = 1; if (n > m) swap(n, m);
for (unsigned i(2); i <= m; ++i) {
if (!No[i]) Prime[++Cnt] = i, Mu[i] = -1;
for (unsigned j(1), Des(i << 1); (j <= Cnt) && (Des <= m); ++j, Des = Prime[j] * i) {
No[Des] = 1, Mu[Des] = Mu[i] * Mu[Prime[j]];
if (!(i % Prime[j])) { Mu[Des] = 0; break; }
}
}
for (unsigned i(1); i <= m; ++i) { Mu[i] = (Mu[i - 1] + Mu[i] * i * i) % Mod; if (Mu[i] < 0) Mu[i] += Mod; }
for (unsigned i(1); i <= n; ++i, Tmp = 0) {
long long Nd(n / i), Md(m / i), Dn(Nd), Dm(Md);
for (long long L(0), R(0); R < Nd;) {
L = R + 1, Dn = Nd / L, Dm = Md / L;
R = min(Nd, min(Nd / Dn, Md / Dm));
Tmp = (Tmp + (((((Mod + Mu[R] - Mu[L - 1]) * (Dn + 1) % Mod) * (Dm + 1) % Mod) * Dn % Mod) * Dm % Mod) * Inv) % Mod;
}
Ans = (Ans + i * Tmp) % Mod;
}
printf("%lld\n", Ans);
return Wild_Donkey;
}
SDOI2015
定义 d(x) 表示 x 的约数个数, 给定 n, m, 求:
\sum_{i = 1}^{n} \sum_{j = 1}^{m} d(ij)\\
约数个数很容易想到狄利克雷卷积的形式, 于是继续推导:
\sum_{i = 1}^{n} \sum_{j = 1}^{m} d(ij) = \sum_{i = 1}^{n} \sum_{j = 1}^{m} \sum_{k | ij} 1\\
我一开始想到的是下面的式子, 取 k = k_1k_2, 其中 k_1 是 i 的因数, k_2 是 j 的因数.
\sum_{i = 1}^{n} \sum_{j = 1}^{m} \sum_{k_1 | i} \sum_{k_2 | j} 1
虽然任意 i 和 j 的两个因数 k_1, k_2 都满足 k_1k_2 | ij, 但是可能存在不同的两组 k_1, k_2 得到相同的乘积的情况, 所以会算重.
如果对于每个质数 p_t, 它在 i 中的次数是 a_t, 在 j 中的次数是 b_t, 在 k 中的次数是 c_t. 把 c_t 分给 k_1 中 d_t 个, 分给 k_2 中 c_t - d_t. 我们之前算重的情况就是出现了 c_t 对应多个 d_t 的情况.
我们为了给 c_t 确定唯一的 d_t, 当 c_t \leq a_t 时, 取 d_t = c_t. 当 c_t > a_t 时, 取 d_t = a_t.
现在考虑如何计数. 根据上面的策略可以把每一个三元组 (i, j, k) 找到唯一的 k_1, k_2 与其对应. 当 k_2 能被 p_t 整除的时候, 可以断定这个时候 d_t = a_t. 如果这时对于所有满足 p_t | k_2 的 t, 定义 k_3 = \frac{k_1}{{p_t}^{a_t}}, 一定有 gcd(k_3, k_2) = 1. 现在 (i, j, k)对应唯一的 (k_3, k_2). 已知变换规则 i, j 不变时, 所有互质的 k_2 | j, k_3 | i 可以得到唯一的 (k_1, k_2), 所以可以得到唯一的 k = k_1k_2.
问题转化为对每个 i, j 求所有满足 k_2 | j, k_3 | i, gcd(k_2, k_3) = 1 的 (k_2, k_3) 的数量.
\begin{aligned}
&\sum_{i = 1}^n \sum_{j = 1}^m \sum_{k_3 | i} \sum_{k_2 | j} [gcd(k_3, k_2) = 1]\\
= &\sum_{k_3 = 1}^n \sum_{k_2 = 1}^m [gcd(k_3, k_2) = 1] \lfloor \frac n{k_3} \rfloor\lfloor \frac m{k_2} \rfloor\\
= &\sum_{d = 1}^n \mu(d) \sum_{k_3 = 1}^{\lfloor \frac nd \rfloor} \sum_{k_2 = 1}^{\lfloor \frac md \rfloor} \lfloor \frac n{k_3d} \rfloor\lfloor \frac m{k_2d} \rfloor\\
= &\sum_{d = 1}^n \mu(d) (\sum_{k_3 = 1}^{\lfloor \frac nd \rfloor}\lfloor \frac n{k_3d} \rfloor) (\sum_{k_2 = 1}^{\lfloor \frac md \rfloor} \lfloor \frac m{k_2d} \rfloor)\\
= &\sum_{d = 1}^n \mu(d) (\sum_{k_3 = 1}^{\lfloor \frac nd \rfloor}\lfloor \frac {\lfloor \frac nd \rfloor}{k_3}\rfloor) (\sum_{k_2 = 1}^{\lfloor \frac md \rfloor} \lfloor \frac {\lfloor \frac md \rfloor}{k_2}\rfloor)\\
\end{aligned}
设:
f(x) = \sum_{i = 1}^x \lfloor \frac xi \rfloor
我们可以 O(\max(n, m)\sqrt{\max(n, m)}) 地预处理所有的 f, 然后就可以变成求:
\sum_{d = 1}^n \mu(d) f(\lfloor \frac nd \rfloor)f(\lfloor\frac md \rfloor)\\
现在已经把式子优化到 O(\min(n, m)), 但是十分遗憾, 这个题是多组数据, 所以即使是这样也无法通过, 显然我们用整除分块可以 O(T\sqrt{\min(n, m)}) 轻松解决此题.
long long f[50005], Mu[50005], Ans(0), Tmp(0);
unsigned Prime[50005], Cnt(0), m, n;
unsigned A, B, C, D, t;
bitset<50005> No;
inline void Clr() {
n = RD(), m = RD(), Ans = 0; if (m < n) swap(n, m);
}
signed main() {
for (unsigned i(1); i <= 50000; ++i) for (unsigned L(0), R(0), Div(0); R < i;)
L = R + 1, Div = i / L, R = i / Div, f[i] += (R - L + 1) * Div;
for (unsigned i(2); i <= 50000; ++i) {
if (!No[i]) Prime[++Cnt] = i, Mu[i] = -1;
for (unsigned j(1), Des(i* Prime[j]); (j <= Cnt) && (Des <= 50000); ++j, Des = i * Prime[j]) {
No[Des] = 1, Mu[Des] = Mu[i] * Mu[Prime[j]];
if (!(i % Prime[j])) { Mu[Des] = 0; break; }
}
}
t = RD(), Mu[1] = 1;
for (unsigned i(2); i <= 50000; ++i) Mu[i] += Mu[i - 1];
for (unsigned T(1); T <= t; ++T) {
Clr();
for (unsigned L(0), R(0); R < n;)
L = R + 1, A = n / L, B = m / L, R = min(n / A, m / B), Ans += (Mu[R] - Mu[L - 1]) * f[A] * f[B];
printf("%lld\n", Ans);
}
return Wild_Donkey;
}
Day29: 线性代数 (Linear Algebra)
线性代数是关于向量空间和线性映射的一个数学分支. 它包括对线, 面和子空间的研究, 同时也涉及到所有的向量空间的一般性质. ----Wikipedia
Vector
任意 n 维向量 (Vector) (a_0, a_1, a_2,...,a_{n - 1}), (b_0, b_1, b_2,...,b_{n - 1}), 其点乘定义为 \prod_{i = 0}^{n - 1} a_i + \prod_{i = 0}^{n - 1} b_i.
对于三维向量 (x_0, y_0, z_0), (x_1, y_1, z_1), 其叉乘定义为两个向量所在平面的法向量, 模长是两个向量决定的平行四边形的面积. 即为 (y_0z_1 - z_0y_1, z_0x_1 - x_0z_1, x_0y_1 - y_0x_1). 在右手系内, 对于法向量的方向, 可以用右手定则判断. 如果是左手系则用左手定则判断. 如果是二维向量, 可以将其作为第三维为 0 的向量做叉乘, 得到的向量关于两个向量所在平面垂直, 也就是关于 x 轴, y 轴所在平面垂直, 所以它的前两维一定是 0, 我们取它的第三维坐标作为二维向量叉乘的结果.
叉乘的反交换律可以表示为:
\vec a \times \vec b = -\vec a \times \vec b
System of linear equations
主要用高斯消元 (Gaussian Elimination) 来求解线性方程组(System of linear equations).
一个 n 未知数的线性方程组有唯一解, 需要存在 n 个线性无关的方程.
对于有 n 个未知数, n 个方程的线性方程组, 我们使得矩阵的第 i 行第 n + 1 列为第 i 个方程等号右边的常数. 前 n 列中, 第 i 行第 j 列表示第 i 个方程中第 j 个未知数的系数.
对于线性方程组的增广矩阵, 我们可以进行如下变换并且解不变:
我们把除第一行以外的行都减去第一行的特定倍数, 使得除第一行以外的每一行的第一项都为 0. 用同样的方法把 [3, n] 的第 2 项变成 0. 最后得到了第 i 行的前 i - 1 项为 0 的矩阵.
然后反过来, 把前 n - 1 行减去对应倍数的第 n 行, 就可以消掉前 n - 1 行的第 n 项. 以此类推可以让第 i 行只剩下第 i 列和第 n + 1 列. 最后只需要把所有行乘以对应倍数使得第 i 列为 1, 这时第 i 行的第 n + 1 列就是解中第 i 个未知数的值了.
复杂度 O(n^3). 下面是模板题代码:
double a[105][105];
unsigned m, n;
unsigned A, B, C, D, t;
unsigned Cnt(0), Ans(0), Tmp(0);
inline char Zer(double& x) { return (x <= 0.00000001) && (x >= -0.00000001); }
signed main() {
n = RD();
for (unsigned i(1); i <= n; ++i) for (unsigned j(1); j <= n + 1; ++j) a[i][j] = RDsg();
for (unsigned i(1); i <= n; ++i) {
unsigned Do(i);
while ((Zer(a[Do][i])) && (Do <= n)) ++Do;
if (Do > n) { printf("No Solution\n");return 0; }
if (Do ^ i) for (unsigned j(i); j <= n + 1; ++j) swap(a[i][j], a[Do][j]);
for (unsigned j(i + 1); j <= n; ++j) {
double Tms(-a[j][i] / a[i][i]);
for (unsigned k(i); k <= n + 1; ++k) a[j][k] += a[i][k] * Tms;
}
}
for (unsigned i(n); i; --i) {
if (Zer(a[i][i])) { printf("No Solution\n");return 0; }
for (unsigned j(i - 1); j; --j)
a[j][n + 1] -= (a[j][i] / a[i][i]) * a[i][n + 1], a[j][i] = 0;
}
for (unsigned i(1); i <= n; ++i) printf("%.2lf\n", a[i][n + 1] / a[i][i]);
return Wild_Donkey;
}
Determinant
对于一个 n 阶方阵 (行列相等的矩阵) A, 定义 \det(A) 表示它的行列式 (Determinant). 如果认为 S_n 是 [1, n] 中正整数的所有 n! 种置换的集合. \mathrm{sgn}(\sigma) 在 \sigma 为奇排列时为 -1, 是偶排列时是 1, 那么方阵 A 的行列式可以表示为:
\det(A) = \sum_{\sigma \in S_n} \mathrm{sgn}(\sigma) \prod_{i = 1}^n A_{i, \sigma(i)}
如果直接求那复杂度将是 O(n!n) 的, 我们仍然使用高斯消元. 其原理是:
-
任意两行(列)交换, 结果取反
-
某行(列)加减另一行(列), 结果不变
-
某行(列)乘以 k 倍, 结果乘以 k
我们用前面的变换将矩阵只留下第 i 行后 i 项的过程中记一下结果会变成之前的多少倍即可.
然后是求行列式, 发现所有第 i 项不是 i 的置换都不需要枚举了, 因为它的 \prod 中一定有至少一项是 0, 对结果没有贡献. 我们只要对这个矩阵对角线上的元素求积即可.
当需要取模时, 模数任意的情况下我们可能无法找到所需的逆元, 所以我们采用辗转相减法进行消元. 两行之间的减法是 O(n) 的, 每次消掉一个位置的元素需要 O(\log p) 次减法. 一共需要消 O(n^2) 个元素, 所以复杂度是 O(n^3\log p). 但是因为我们是连续消掉一列的元素, 每次相减后, 对应位置剩下的元素是上面所有元素的 GCD, 所以消掉一列元素均摊需要 O(n + \log p) 次减法, 因此更精确的复杂度应该是 O(n^2(n + \log p)).
下面是模板题代码:
unsigned long long Gcd(unsigned long long x, unsigned long long y) {
unsigned long long SwT;
while (y) SwT = x, x = y, y = SwT % y;
return x;
}
unsigned long long a[605][605], Mod, G, Tms(1), Ans(1);
unsigned m, n;
unsigned A, B, C, D, t;
unsigned Cnt(0);
inline void Dec(unsigned long long* f, unsigned long long* g, unsigned x) {
while (g[x]) {
unsigned long long Tmp(Mod - (f[x] / g[x]));
for (unsigned i(x); i <= n; ++i) f[i] = (f[i] + g[i] * Tmp) % Mod;
for (unsigned i(x); i <= n; ++i) swap(f[i], g[i]);
Tms = Mod - Tms;
}
}
signed main() {
n = RD(), Mod = RD();
for (unsigned i(1); i <= n; ++i) for (unsigned j(1); j <= n; ++j) a[i][j] = RD() % Mod;
if (n == 1) { printf("%llu\n", a[1][1]);return 0; }
for (unsigned i(1); i <= n; ++i) {
G = Gcd(a[i][1], a[i][2]);
for (unsigned j(3); j <= n; ++j) G = Gcd(G, a[i][j]);
if (G > 1) for (unsigned j(1); j <= n; ++j) a[i][j] /= G;
Tms = Tms * G % Mod;
}
for (unsigned i(1); i <= n; ++i) {
G = Gcd(a[1][i], a[2][i]);
for (unsigned j(3); j <= n; ++j) G = Gcd(G, a[j][i]);
if (G > 1) for (unsigned j(1); j <= n; ++j) a[j][i] /= G;
Tms = Tms * G % Mod;
}
for (unsigned i(1); i <= n; ++i) for (unsigned j(n); j > i; --j) if (a[j][i]) Dec(a[j - 1], a[j], i);
for (unsigned i(1); i <= n; ++i) Ans = Ans * a[i][i] % Mod;
printf("%llu\n", Ans * Tms % Mod);
return Wild_Donkey;
}
Matrix Multiplication
对于 m 行 n 列的矩阵 A, n 行 o 列的矩阵 B, 定义矩阵乘法运算为:
[AB]_{i,j} = \sum_{k = 1}^n A_{i,k}B_{k,j}
矩阵乘法的单位矩阵 $I_n$ 是一个 $n * n$ 的矩阵, 其左上右下对角线为 $1$, 其余部分为 $0$. 满足对于任意有 $n$ 列的矩阵 $A$, $AI = A$, 对于任意有 $n$ 行的矩阵 $B$, $IB = B$.
### Inverse Matrix
一个矩阵的乘法逆元是它的逆矩阵 (Inverse Matrix), 只有方阵存在逆矩阵, 定义 $A^{-1}A = I$.
我们把 $A$ 和 $I$ 并排放在一起, 组成 $n$ 行, $2n$ 列的矩阵. 用高斯消元把第 $i$ 行除第 $i$ 项和后 $n$ 项以外的项变成 $0$. 然后第 $i$ 行乘以相应的倍数把第 $i$ 项变成 $1$. 只要得到的左边 $n$ 列是 $I$, 那么右边 $n$ 列就是 $A^{-1}$.
求逆矩阵的过程就是高斯消元的过程, 复杂度 $O(n^3)$. 下面是[模板题](https://www.luogu.com.cn/problem/P4783)代码:
```cpp
const unsigned long long Mod(1000000007);
unsigned long long a[405][805];
unsigned A, B, C, D, t, m, n;
unsigned Cnt(0), Ans(0), Tmp(0);
unsigned long long Pow(unsigned long long x, unsigned y) {
unsigned long long Rt(1);
while (y) { if (y & 1) Rt = Rt * x % Mod; x = x * x % Mod, y >>= 1; }
return Rt;
}
signed main() {
m = ((n = RD()) << 1);
for (unsigned i(1); i <= n; ++i) for (unsigned j(1); j <= n; ++j) a[i][j] = RD();
for (unsigned i(1); i <= n; ++i) for (unsigned j(n + 1); j <= m; ++j) a[i][j] = 0;
for (unsigned i(1); i <= n; ++i) a[i][n + i] = 1;
for (unsigned i(1); i <= n; ++i) {
unsigned No(i);
while ((!a[No][i]) && (No <= n)) ++No;
if (No > n) { printf("No Solution\n");return 0; }
if (No ^ i) for (unsigned j(i); j <= m; ++j) swap(a[No][j], a[i][j]);
for (unsigned j(i + 1); j <= n; ++j) {
unsigned long long Tms(a[j][i] * (Mod - Pow(a[i][i], Mod - 2)) % Mod);
for (unsigned k(i); k <= m; ++k) a[j][k] = (a[j][k] + a[i][k] * Tms) % Mod;
}
}
for (unsigned i(n); i; --i) {
if (!a[i][i]) { printf("No Solution\n");return 0; }
unsigned long long Chg(Pow(a[i][i], Mod - 2));
if (Chg != 1) for (unsigned j(i); j <= m; ++j) a[i][j] = a[i][j] * Chg % Mod;
for (unsigned j(i - 1); j; --j) {
for (unsigned k(n + 1); k <= m; ++k) a[j][k] = (a[j][k] + a[i][k] * (Mod - a[j][i])) % Mod;
a[j][i] = 0;
}
}
for (unsigned i(1); i <= n; ++i) { for (unsigned j(n + 1); j <= m; ++j) printf("%llu ", a[i][j]); putchar(0x0A); }
return Wild_Donkey;
}
```
### Rank
矩阵的秩 (Rank) 定义为最多找出多少行使得它们两两线性无关. 一个矩阵的秩等于它转置矩阵的秩. 把一个矩阵高斯消元后不全为 $0$ 的行的数量就是这个矩阵的秩.
### Kirchhoff's Theorem
基尔霍夫定理 (Kirchhoff's Theorem), 因为是用矩阵求无向图的所有本质不同的生成树的数量, 所以又叫矩阵树定理 (Matrix Tree Theorem):
构造一个矩阵, 对角线上 $(i, i)$ 是第 $i$ 个点的度, 两个点 $i$, $j$ 之间连边就将 $(i, j)$ 和 $(j, i)$ 设为 $-1$. 钦定一个点为根, 则删掉这个点对应的行和列, 矩阵的行列式就是需要求的答案.
对于有向图, $(i, i)$ 记录出度, 每条从 $i$ 到 $j$ 的有向边将 $(i, j)$ 置为 $-1$. 需要枚举每个点作为根求行列式, 然后求和.
如果存在自环, 直接忽略这种边, 因为无论什么生成树都不可能包含自环边. 如果有重边, 我们可以认为这两个点之间有边的情况都要被计数两次, 分别给两个点的度数在之前的基础上再加一, 邻接矩阵上也再减一. 如果把重边看成是带权的边, 有几条重边边权就是几, 那么求得的行列式就是所有生成树的边权之积的总和. 发现两种情况是等价的.
对于带权图, 只要把 $-1$ 设为负的两点间边权总和, 让每条边对度数的共献为边权, 就可以求出每棵生成树的边权积之和了. 有向图也存在类似的结论.
下面是[模板题](https://www.luogu.com.cn/problem/P6178)代码:
```cpp
const unsigned long long Mod(1000000007);
unsigned long long a[305][305], Tms(1);
unsigned m, n;
unsigned A, B, C, D, t;
unsigned Cnt(0), Ans(1);
char Opt;
inline unsigned long long Pow(unsigned long long x, unsigned y) {
unsigned long long Rt(1);
while (y) { if (y & 1) Rt = Rt * x % Mod; x = x * x % Mod, y >>= 1; }
return Rt;
}
signed main() {
n = RD() - 1, m = RD(), Opt = RD();
for (unsigned i(1); i <= m; ++i) {
A = RD() - 1, B = RD() - 1, C = RD();
if (A ^ B) {
a[B][B] += C, a[A][B] += Mod - C;
if (!Opt) a[A][A] += C, a[B][A] += Mod - C;
}
}
for (unsigned i(1); i <= n; ++i) for (unsigned j(1); j <= n; ++j) a[i][j] %= Mod;
for (unsigned i(1); i <= n; ++i) {
unsigned No(i);
while ((No <= n) && (!a[No][i])) ++No;
if (No > n) { printf("0\n"); return 0; }
if (No ^ i) { for (unsigned j(i); j <= n; ++j) swap(a[No][j], a[i][j]); Tms = Mod - Tms; }
for (unsigned j(i + 1); j <= n; ++j) {
unsigned long long Tmp(a[j][i] * (Mod - Pow(a[i][i], Mod - 2)) % Mod);
for (unsigned k(i); k <= n; ++k) a[j][k] = (a[j][k] + a[i][k] * Tmp) % Mod;
}
}
for (unsigned i(1); i <= n; ++i) Ans = Ans * a[i][i] % Mod;
printf("%llu\n", Ans * Tms % Mod);
return Wild_Donkey;
}
```
## Day30: 欢乐模拟赛
### A
求最大非空子段和.
没读题亏死, "非空" 子段, 所以需要在最大子段和的程序上略加修改, 使得枚举的元素必选, 避免空选.
幸亏只挂了 $10'$.
```cpp
unsigned n;
long long a[1000005], K, B, Cnt(0), A, Ans(-0x3f3f3f3f3f3f3f3f), Tmp(0);
inline void Clr() {}
int main() {
n = RD(), K = RDsg(), B = RDsg();
for (register unsigned i(1); i <= n; ++i) {
a[i] = RDsg() * K;
}
Ans = Tmp = a[1];
for (register unsigned i(2); i <= n; ++i) {
Tmp += a[i];
if(Tmp < a[i]) Tmp = a[i];
Ans = max(Ans, Tmp);
}
printf("%lld\n", Ans + B);
// }
return Wild_Donkey;
}
```
### B
貌似可以 $O(n)$, 但是场上想的 $O(n \log n)$, 所以就写了, 而且飞快.
因为有两个值, 生命和收益, 给两个值做前缀和, 记为 $H$, $W$. 因为收益单调不减, 所以固定左端点, 不死亡的前提下尽可能多走一定不会更劣.
而左端点 $i$ 选在 $H$ 连续下降的末尾一定是极优的, 因为 $H_i < H_{i - 1}$, 所以选 $i - 1$ 相当于上来就直接去世. 而 $H_i \leq H_{i + 1}$, 所以选 $i$ 相当于比 $i + 1$ 多回了一次血或者多收益了一个单位.
接下来需要求固定左端点 $i$ 的不死亡最远点 $j$, 也就是右端点, 而这个左端点对应的答案就是 $W_j - W_{i - 1}$.
枚举左端点, 如果左端点为 $i$, 则右端点 $j$ 是 $j > i$ 的第一个 $H_j < H_i$ 的位置 $-1$.
使用 ST 查询 $H_i$ 的区间最小值, 然后二分右端点 $j$, 判断 $[i, j]$ 的最小值是否是 $H_i$, 如果是, 说明 $j$ 合法, 否则 $j$ 取大了.
ST 预处理 $O(n \log n)$, 枚举左端点 $O(n)$, 二分右端点 $O(\log n)$, 单次判断 $O(1)$, 总复杂度 $O(n \log n)$.
```cpp
int Pre[1000005][21];
unsigned m, n(1), Sum[1000005], Log[1000005], Bin[25], Cnt(0), A, B, C, D, t, Ans(0), Tmp(0);
char a[1000005];
int Find(unsigned L, unsigned R) {
register unsigned TmpF(Log[R - L + 1]);
return min(Pre[L][TmpF], Pre[R - Bin[TmpF] + 1][TmpF]);
}
int main() {
fread(a + 2, 1, 1000001, stdin);
for (; a[n + 1] >= 'A'; ++n) a[n] -= 'A';
a[n] -= 'A';
if(n == 1) {
if(a[1] == 0) Ans = 1;
printf("%u\n", Ans);
return 0;
}
for (register unsigned i(1), j(0); i <= n; ++j, i <<= 1) {
Log[i] = j, Bin[j] = i;
}
for (register unsigned i(1); i <= n; ++i) {
Log[i] = max(Log[i], Log[i - 1]);
}
Pre[0][0] = 0x3f3f3f3f, Pre[1][0] = 1, Sum[0] = 0;
for (register unsigned i(2); i <= n; ++i) {
Sum[i] = Sum[i - 1];
Pre[i][0] = Pre[i - 1][0];
if(!a[i]) ++Sum[i];
else {
if(a[i] ^ 1) ++Pre[i][0];
else --Pre[i][0];
}
}
for (register unsigned i(1), j(0); i < n; i <<= 1, ++j) {
for (register unsigned k(1); k + i <= n; ++k) {
Pre[k][j + 1] = min(Pre[k][j], Pre[k + i][j]);
}
}
for (register unsigned i(1); i + 2 <= n; ++i) {
if((Pre[i][0] < Pre[i - 1][0]) && (Pre[i][0] <= Pre[i + 1][0])) {
register unsigned L(i + 2), R(n), Mid;
while (L < R) {
Mid = ((L + R + 1) >> 1);
if(Pre[i][0] > Find(i, Mid)) {
R = Mid - 1;
} else {
L = Mid;
}
}
Ans = max(Ans, Sum[L] - Sum[i - 1]);
}
}
if(Sum[n - 1] - Sum[n - 2]) Ans = max(Ans, (unsigned)1);
if(Sum[n] - Sum[n - 1]) {
Ans = max(Ans, (unsigned)1);
if(Sum[n - 1] - Sum[n - 2]) Ans = max(Ans, (unsigned)2);
}
printf("%u\n", Ans);
return Wild_Donkey;
}
```
接下来是线性算法, 我们将之前枚举的极优左端点称为 "谷点", 考虑谷点的优劣关系, 如果一个谷点 $i_1 < i_2$, 且 $H_{i_1} < H_{i_2}$, 这时 $[i_2, j_2] \subset [i_1, j_1]$, 所以 $i_1$ 一定不比 $i_2$ 劣.
所以可能更新答案的谷点, 一定满足 $H$ 值随下标的增加而单调不增.
而这些谷点所对应的右端点是单调递增的, 所以可以双指针扫描整个数组, 总复杂度 $O(n)$.
```cpp
int Pre[1000005], Last(0x3f3f3f3f);
unsigned m, n(1), Sum[1000005], Cnt(0), A, B, C, D, t, Ans(0), Tmp(0);
char a[1000005];
int main() {
fread(a + 2, 1, 1000001, stdin);
for (; a[n + 1] >= 'A'; ++n) a[n] -= 'A';
a[n] -= 'A';
if(n == 1) {
if(a[1] == 0) Ans = 1;
printf("%u\n", Ans);
return 0;
}
Pre[0] = 0x3f3f3f3f, Pre[1] = 1, Sum[0] = 0;
for (register unsigned i(2); i <= n; ++i) {
Sum[i] = Sum[i - 1];
Pre[i] = Pre[i - 1];
if(!a[i]) ++Sum[i];
else {
if(a[i] ^ 1) ++Pre[i];
else --Pre[i];
}
}
for (register unsigned i(1), j; i <= n; ++i) {
if((Pre[i] < Pre[i - 1]) && (Pre[i] <= Pre[i + 1])) {
if(Pre[i] <= Last) {
Last = Pre[i];
for (j = i; (j < n) && (Pre[j] >= Pre[i]); ++j);
Ans = max(Ans, Sum[j] - Sum[i - 1]);
if(j > i) i = j - 1;
else i = j;
}
}
}
printf("%u\n", Ans);
return Wild_Donkey;
}
```
仍然有一种想法, 扫描的时候开一个 $Pre$ 数组记录最后一次前缀和出现这个值的位置
### C
讨论题.
首先可以发现, 一个点是前三名, 所有可到达这个点的点一定需要小于 $3$, 否则一定不合法. 所以所有入度大于等于 $3$ 的点都是废点, 不会被答案统计到, 并且所有它到达的点都是废点.
然后建分层图, 发现分层图中有用的节点最多只有 $3$ 层.
分析可能前三的点组成的性质:
- 每层节点内部没有连边
- 第一层节点入度为 $0
-
第二层节点入度为 1 或 2
-
第二层的点入度为 2 的情况下不能有出边
-
第三层节点的入度要么为 1, 要么入度为 2 的情况下满足两条入边起点中间也有连边, 深度分别是 1, 2, 也就是 a>b, b>c, a>c 三个约束同时出现, 这时可以直接删除 a>c 这条边. 所以可以认为最后分层图中第三层的点合法入度为 1.
然后对于每种情况分析答案数量:
这种情况是指指定一个第三层的点作为第三名, 由于它只有一个入度, 来自一个第二层的点, 于是选中这个点作为第二名, 因为有出度的第二层的点只有一个入度, 所以最后一个作为第一名的点也确定了. 所以每个第三层的点对应一个 1, 2, 3 方案. 剩下的情况都不含第三层的点.
这种情况选定了一个第一层的点做第一名, 然后任选两个入度为 1 的第二层点做第二和第三. 假设一个第一层的点出边连向 x 个入度为 1 的第二层的点, 那么这个点对 1, 2, 2 方案贡献的答案就是 A_2^x, 也就是 x(x - 1).
这是针对入度为 2 的第二层的点的, 选定一个入度为二的第二层的点做第三名, 它的两条入边对应的两个第一层的点分别做第一和第二, 每个入度为 2 的第二层的点对应 2 中方案.
这种方案选择了一个第一层的点, 一个它出边对应的入度为 1 的第二层的点, 然后任选另外一个第一层的点, 分别作第一, 第二, 第三. 一开始选定的两个点按顺序做剩下的两名. 假设第一层有 y 个点, 那么每个入度为 1 的第二层的点都会对答案做出 3(y - 1) 个贡献.
三个入度为零的点任意组合, 假设有 y 个入度为 0 的点, 则对答案贡献为 A^y_3[y \geq 3].
考场上得了 20', 原因是将第三层的入度大于 1 的点一棍子打死了, 没有考虑 a>b, b>c, a>c 也是可行的, 漏掉了 a 第一, b 第二, c第三的答案.
改了一下午变成 30', 原因是将所有第三层入度为 2 的点, 只要满足两个入度对应的点有约束关系就放走了, 以至于将 a>b, b>c, a>c, d>b 数据中的 c 放走了, 需要判断每个点的入度再讨论是否放走.
实现方面, 一开始从所有入度为 0 的点多源 BFS, 一边分层一边删除点. 然后在所有打 Ava 标记的可行点组成的分层图上以每个点为跑 DFS, 然后统计五种答案.
复杂度也很简单, 一开始排序去重 O(m \log m), BFS 时每个点都会入队一次, 遍历所有的边, O(n + m), DFS 的时候, 一个第三层的点只会被一个第一层的点搜到, 而一个第二层的点最多被搜到两次, 所以复杂度 O(n). 总复杂度 O(m \log m + n).
struct EdIn {
unsigned Fr, To;
inline const char operator < (const EdIn &x) const {
return (this->Fr ^ x.Fr) ? (this->Fr < x.Fr) : (this->To < x.To);
}
inline const char operator == (const EdIn &x) const {
return (this->Fr == x.Fr) && (this->To == x.To);
}
}EI[200005];
struct Edge;
struct Node {
Node *In1, *In2;
char Ava;
unsigned Dep, ID, OD;
Edge *Fst;
}N[100005], *Q[100005];
inline void Print(Node *x) {
printf("Node %u ID %u OD %u Ava %u Dep %u\n", x - N, x->ID, x->OD, x->Ava, x->Dep);
printf("In1 %u In2 %u\n", x->In1 - N, x->In2 - N);
}
struct Edge {
Node *To;
Edge *Nxt;
}E[200005];
unsigned m, n, Hd, Tl;
unsigned long long Cnt(0), Cnt0(0), Ans(0);
void DFS (Node *x) {
register Edge *Sid(x->Fst);
register unsigned TA(0);
while (Sid) {
if(Sid->To->Ava) {
++(x->OD);
if((Sid->To->Dep == 2) && (Sid->To->ID == 1)) DFS(Sid->To);
if(x->Dep == 1) {
if(Sid->To->ID == 2) ++Ans;// 1, 1, 2
else {
Ans += Sid->To->OD;// 1, 2, 3
Ans += 3 * (Cnt0 - 1); // 1, 2 + 1
++TA; // 1, 2, 2
}
}
}
Sid = Sid->Nxt;
}
Ans += ((unsigned long long)TA * (TA - 1));
}
int main() {
n = RD(), m = RD();
for (register unsigned i(1); i <= m; ++i) {
EI[i].Fr = RD(), EI[i].To = RD();
}
sort(EI + 1, EI + m + 1);
m = unique(EI + 1, EI + m + 1) - EI - 1;
for (register unsigned i(1); i <= m; ++i) {
++N[EI[i].To].ID;
E[i].Nxt = N[EI[i].Fr].Fst;
N[EI[i].Fr].Fst = E + i;
E[i].To = N + EI[i].To;
if(N[EI[i].To].In1) N[EI[i].To].In2 = EI[i].Fr + N;
else N[EI[i].To].In1 = EI[i].Fr + N;
}
Hd = Tl = 0;
for (register unsigned i(1); i <= n; ++i) if(!(N[i].ID)) {
++Cnt0, N[i].Dep = 1, Q[++Tl] = N + i, N[i].Ava = 1;
continue;
}
if(Cnt0 >= 3) Ans = (unsigned long long)Cnt0 * (Cnt0 - 1) * (Cnt0 - 2);
register Node *Now;
register Edge *Sid;
while (Hd < Tl) {
Now = Q[++Hd], Sid = Now->Fst;
while (Sid) {
if(!(Sid->To->Dep)) {
Sid->To->Dep = Now->Dep + 1;
Q[++Tl] = Sid->To;
if(Now->Dep == 1) {
if(Sid->To->ID <= 2) {
Sid->To->Ava = 1, Sid = Sid->Nxt;
continue;
}
} else {
if((Sid->To->ID == 1) && (Now->Dep == 2)) { // Available
Sid->To->Ava = 1, Sid = Sid->Nxt;
continue;
}
}
} else {// Visited
Sid->To->Dep = Now->Dep + 1;
if(Sid->To->Dep > 3) {
Sid->To->Ava = 0;
Sid = Sid->Nxt;
continue;
}
if(Sid->To->Dep == 3) {
if((Now->ID == 1) && (Sid->To->ID == 2)) { // Available
if(Sid->To->In1 == Now) {
if((Sid->To->In2 == Now->In1) || (Sid->To->In2 == Now->In2)) {
Sid->To->Ava = 1, --(Now->OD), Sid = Sid->Nxt;
continue;
}
} else {
if((Sid->To->In1 == Now->In1) || (Sid->To->In1 == Now->In2)) {
Sid->To->Ava = 1, --(Now->OD), Sid = Sid->Nxt;
continue;
}
}
}
Sid->To->Ava = 0;
}
}
Sid = Sid->Nxt;
}
}
for (register unsigned i(1); i <= n; ++i) if(!(N[i].ID)) DFS(N + i);
printf("%llu\n", Ans);
return Wild_Donkey;
}
D
给一棵无根树, 每条边权有 \frac 12 的概率为 1, 剩下 \frac 12 的概率为 2. 求其直径的期望. 点数不超过 60.
一开始想直接求每个子树的直径的期望和最深叶子的深度期望来合并, 但是被第二个样例叉掉了.
设计状态 f_{i, j, k}, 表示第 i 个点的子树, 最深的叶子到自己的距离为 j, 子树直径是 k 的概率.
转移就是每次遍历 i 的一个儿子 Son 之后, 将 Son 的信息合并到 i 上. 两行分别对应 i 到 Son 的边取 0 和 1 的情况.
f_{i, \max(Sm + 1, Mem), \max(Med, Sm + Mem + 1, Sd)} += \frac{f_{Son, Sm, Sd} * f_{i, Mem, Med}}2\\
f_{i, \max(Sm + 2, Mem), \max(Med, Sm + Mem + 2, Sd)} += \frac{f_{Son, Sm, Sd} * f_{i, Mem, Med}}2
答案是
\sum_i i \sum_j f_{1, j, i}
状态 O(n^3), 转移 O(n^2), 复杂度 O(n^5).
因为所有边取两个值的概率是 \frac 12, 所以所有 DP 值一定可以用自然数 a, b 表示为 \frac a{2^b}. 而且 b < n \leq 60, 所以我们可以用 unsigned long long 代替 double. 虽然占内存空间相同, 但是运算效率更高, 而且没有精度问题. 只需要保存 DP 值的 2^{63} 倍, 这个值一定是自然数, 在乘法运算时需要把结果除以 2^{63}.
虽然这个题的复杂度算出来很大 (7.7*10^8), 但是实际上跑得飞快 (50 个点跑了约 20ms).
#define Lbt(x) ((x)&((~(x))+1))
unsigned long long T63((unsigned long long)1 << 63);
double Ans(0);
unsigned a[10005], m, n;
unsigned A, B, C, D, t;
unsigned Cnt(0);
struct Node {
vector <Node*> Son;
unsigned long long f[120][120];
Node* Fa;
unsigned Dep, Len;
}N[65];
inline unsigned long long Mul(unsigned long long x, unsigned long long y) {
if ((!x) || (!y)) return 0;
unsigned long long Tm2((T63 / Lbt(x)) << 1);
x /= Lbt(x), y /= Tm2;
return x * y;
}
inline void DFS(Node* x) {
x->Len = x->Dep = 0, x->f[0][0] = ((unsigned long long)1 << 63);
unsigned long long Tmp[120][120];
for (auto i : x->Son) if (i != x->Fa) {
i->Fa = x, DFS(i);
memset(Tmp, 0, sizeof(Tmp));
for (unsigned Mem((x->Dep) << 1); (~Mem) && (Mem >= x->Dep); --Mem) {
for (unsigned Med((x->Len) << 1); (~Med) && (Med >= x->Len); --Med) {
for (unsigned Sm((i->Dep) << 1); (~Sm) && (Sm >= i->Dep); --Sm) {
for (unsigned Sd((i->Len) << 1); (~Sd) && (Sd >= i->Len); --Sd) {
unsigned long long Mt(Mul(x->f[Mem][Med], i->f[Sm][Sd]));
Tmp[max(Mem, Sm + 1)][max(Mem + Sm + 1, max(Med, Sd))] += Mt;
Tmp[max(Mem, Sm + 2)][max(Mem + Sm + 2, max(Med, Sd))] += Mt;
}
}
}
}
memcpy(x->f, Tmp, sizeof(Tmp));
x->Len = max(x->Len, max(i->Len, x->Dep + i->Dep + 1));
x->Dep = max(x->Dep, i->Dep + 1);
}
}
signed main() {
n = RD();
for (unsigned i(1); i < n; ++i) A = RD(), B = RD(), N[A].Son.push_back(N + B), N[B].Son.push_back(N + A);
DFS(N + 1);
for (unsigned Mem((N[1].Dep) << 1); Mem >= N[1].Dep; --Mem) {
for (unsigned Med((N[1].Len) << 1); Med >= N[1].Len; --Med) {
Ans += ((double)N[1].f[Mem][Med] / T63) * Med;
}
}
printf("%.10lf", Ans);
return Wild_Donkey;
}
完结撒花
暑假的培训 (2021 年 7 月 17 日到 2021 年 8 月 15 日) 仿佛近在眼前, 但是我把这 30 天所学内容整理完的这一天, 是 2022 年 1 月 22 日. Flag 也从 CSP 之前补完, 改到 NOIP 之前补完, 又改到省选前补完. 不过终于是补完了, 三篇 Markdown 的大小达到了 645KB. 一些补题衍生出来的各种算法笔记只是留下了一个链接, 并未收录到笔记本身 (比如为了补 DP 优化现学的卷积), 除了部分板块的题记引用了维基百科的原文, 其他内容都是由我独立完成. 如果你对 645KB 没有概念, 那么一本红楼梦有 78.8 万字, 一个字占两个字节, 也就是大约 1600KB.
第 1-10 天: 传送门
第 11-20 天: 传送门
这次培训让我收获了算法知识, 比赛技巧, 酒量, 友谊甚至还有爱情 (虽然已经没了). 补完了题, 就给这段时光画上一个句号. 在退役后它仍然可以作为一次难忘的 OI 经历被我铭记.