【洛谷日报#161】浅谈在上古题库USACO中的刷题技巧

#### 本文中的$USACO$均指的是$USACO ~training$，此外还有$USACO$月赛题目同样值得去做，本文不做赘述。 # [$\color{violet} ~~~~\mathbb{HERE'S~~MY~ ~BLOG}~~~~$](https://xtzorz.github.io/) ## 前言： 最近在老师的建议~~压迫~~下刷完了$USACO$，我觉得~~题出的好!难度适中,覆盖知识点广,题目又着切合实际的背景,解法比较自然。给出题人点赞 !~~ 可惜的是，随着各大OJ的兴起，$USACO$这个题库却渐渐淡出大家的视野。于是借此机会，由我向大家介绍一下这个美帝的上古题库。 #### 这篇文章您将看到： - 简短的对$USACO$及其题目的介绍 - 对于不同阶段OIer的正确食用方法 - 一些适用于不同阶段OIer的题目典型栗子 顺便附上最终进度：  其中有些题实在太暴力不想打，外加有一道题查看权限没了，所以终究没有AK。。 ## $0.~$更新后的一些修正 好像成功入选洛咕日报了QAQ 看到评论区有人吐槽$training$并不是上古题库一事，这肯定是有些许夸张的因素啦，作者只想表达出$usaco~training$有较长历史这一事实罢了（毕竟十多年肯定是有了）。 至于`淡出大家视野`只是作者处在弱省弱市的环境中从而得出的结论，至于在某些强校仍把usaco作为基础题库训练一事就不得而知了，这里是作者的疏忽但也也是作者作此文的初衷，就不删了。 ## $1.~USACO$及其题目特色 USACO是美国中学生的官方竞赛网站，分为training和月赛两部分，是美国著名在线题库。 — —摘自百度百科 其中$training$部分共分为6章，每章3~4节不等，每节题目1~5不等。扳指算来也不过百题，如果您想挑战usaco题库，对建议在1~2个月内将其大体上做完。 $P.S.~$当然，$USACO$题面中的主角往往会发生在一个叫约翰的农夫以及他的农场中的神仙奶牛身上，这使得很多老辈的OIer看到题面中有奶牛啥的第一反应都会怀疑这是哪年USACO月赛的题目。 --- #### 话说回来，$USACO$的题目质量到底如何呢？ ~~USACO题库是把双刃剑。~~ 我们先说明一下$USACO$有哪些优点： 1. **题目具有梯度**，方便不同阶段的选手选择与自己实力相合的题目进行练习。 2. **涉及大量常用模板**。其中最短路，背包模型，凸包，网络流等至今NOIp和NOI都常考的算法，里面均有涉及。 3. **具有一定思维性。** 在第三章之后的题目基本上是平均蓝题水平的，并不**全**是因为代码长，而是很多毒瘤DP需要花费大量的思维时间。如果您想锻炼自己的脑洞水平，建议对于每题有20分钟充分的思考再去选择题解。 4. **刷题有便捷的途径。** 不同于其他国外题库，USACO题库不需要$remote~judge$，并且在试炼场最下方LG已经良心的整理好了各章节的所有题目，这样就不用担心高阶OIer想要刷难题还要重头从小学题目刷起的尴尬了。 然而$USACO$确实有一些硬伤存在，主要是： 1. 全英文题面看不懂。 其实在洛谷这并不算问题，因为每道题都已经具备了详细的翻译，有些难于理解的地方译者还特别做了注释，~~当然不排除某些OIer是为了学英语去刷USACO~~。 ~~当然这些翻译大部分来源于几年前一个叫NOCOW的网站，可惜如今此网站由于维护不足而报废了。。~~ 2. **题型单一。** 虽说$USACO$已经涉猎一些模板，但却将大量的经历放在深搜和动态规划上，导致一些NOIP常考算法没有提及。**尤其是在数论方面除了盲押一道小凯的疑惑外，基本不涵盖任何内容。** **所以作者的建议是，各位在临近$NOIp$时不要仅刷$USACO$，而忽略了历年的$NOIp$题的存在，毕竟做了多少题都是为了联赛服务的。** 3. **毒瘤的题目描述和输出格式。** 由于上古题库并不具备SPJ，导致很多输出方案的题目总会加入十分繁琐的输出格式增大题目难度。 ~~最出名的是P2724，这道题对输出格式的处理超了主程序十几行，而且各种恶心的小细节让您WA了又WA。讨论贴里面五条有三条是骂输出格式的。~~ 但这些题毕竟占少数，大部分题都是很良心的，甚至有一道题目在原USACO要求输出的方案的顺序，在洛谷由于太过毒瘤就删去了子问题。 ## $2.$ 对不同阶段$OIer$，刷$USACO$的不同策略 听了以上作者对于USACO优缺点的分析，相信您对$USACO$题目的整体水平已经有了一些了解。~~但正所谓 “高处不胜寒”~~ ，一昧地往后刷却不兼顾~~历史的进程~~$NOIp$实际的难度，您是要对自己的成绩负责任的，选择适合自己层次的题目才真正能达到高效刷题。 接下来作者将根据自己刷题的见解对五章节难易度进行划分，请大家根据自己的能力科学选择： 第一章： 主要考察对题面的理解程度和简单模拟暴力，建议语言初学者，普及水平前期OIer食用。 第二章： 已经涉及到BFS洪水填充，基础DP等一些进阶小技巧。对于DP模块不熟练的人还是先去做做01背包等板子题再来碰，建议普及水平中后期的OIer食用。 第三章： 并没有啥新添的，依然是一些DP和暴力。适用于普及后期至提高前期。 **然而第三章与第四章有个断层，从算法难度直接从普及+跳到了省选-。** 建议去学一下提高的一些基础数论，数据结构等（虽然以上算法未必会用到，但是对于国内比赛尤为重要）。 第四章： 涉及到了省选才考的网络流。。但除此之外都是些提高OIer的基础操作。 第五章： 二维凸包板子题，您如果是备考tg的话可不必写。。还涉及了网络流继续入门+DP进阶+数据结构进阶。适用于提高后期至省选前期。 从以上论述来看： - 如果您是普及阶段的OIer，刷至第三章已经达到PJ省一的标准，也可以适当选择后两章的暴力练练手； - 但如果您是提高阶段的OIer且想冲提高省一，最好将五章刷完（如果您觉得第一章过水而不屑于刷，那也请口头AC再跳过）； - 如果您是省选OIer，那这个题库您可以只用做做里面 “提高+/省选” 难度的**动规**即可，因为其他的算法您肯定都能在别的地方找到类似的影子，没有再做的必要了。 ## $3.~$一些不同类型的典型栗子： 为了更全面的熟悉USACO题库的尿性，作者在这里选了4道比较有代表性的题目，难度从`普及-到省选-`不等，让大家对此有一定具体的概念。 当然，短短的4道题并不能涵盖整个题库的内容，~~希望大家不要因为这四道题过于水而产生了USACO全是水题的想法~~。 ## [$\color{purple} eg.1:P2693:[USACO1.3] Combination~ Lock$](https://www.luogu.org/problemnew/show/P2693) **题面：** 农夫约翰知道他的奶牛很聪明，所以他希望确保它们不会在简单地试了很多不同的号码组合之后就能轻易开锁。**锁上有三个转盘，每个上面有数字1..N (1 <= N <= 100)，因为转盘是圆的，所以1和N是相邻的。** 有两种能开锁的号码组合，一种是农夫约翰设定的，还有一种“预设”号码组合是锁匠设定的。但是，锁有一定的容错性，所以，**在每个转盘上的数字都与一个合法的号码组合中相应的数字相距两个位置以内时，锁也会打开。** 比如说，如果农夫约翰的号码组合是(1,2,3)，预设号码组合是(4,5,6)，在转盘被设定为(1,4,5)（因为这和农夫约翰的号码组合足够接近）或(2,4,8)（因为这和预设号码组合足够接近）。注意，(1,5,6)并不会打开锁，因为它与任一号码组合都不够接近。 询问所有不同的能够开锁的号码组合的总数。 **分析：** ~~LG日报讲这么水的题会不会被打。~~ 其实对于普及OIer来说真的就是理解题意的问题了，题面中的关键部分已经加粗，结合下面的例子应该可以做到很快理解。 然后就三重循环暴力枚举可能的方案，然后暴力判断与哪个号码相近即可。。 没有代码。 ## [$\color{purple} eg.2:P2727 ~ Stringsobits$](https://www.luogu.org/problemnew/show/P2727) **题面：** 考虑排好序的N(N<=31)位二进制数。他们是排列好的，而且包含所有长度为N且这个二进制数中1的位数的个数小于等于L(L<=N)的数。 你的任务是输出第i（1<=i<=长度为N的二进制数的个数）小的（注：题目这里表述不清，实际是，从最小的往大的数，数到第i个符合条件的，这个意思），长度为N，且1的位数的个数小于等于L的那个二进制数。 （例：100101中，N=6，含有位数为1的个数为3）。 可能题面第一遍读完并没有懂。。您可以去讨论区里面找找关于样例解释的讨论，很多USACO题目都会有。。 **分析：** USACO对于DP的~~七十二般~~ 变化可谓出神，有很多本文作者想都没想过的清奇思路，这里就挑选一道比较有特点的说一下。 暴力搜肯定是不行的，那就得考虑DP了。求出第i个符合条件的不知道，但设$f[i][j]$为长度为i，含有j个”1”的个数，求这个还是很好想的: $$f[i][j]=f[i-1][j]+f[i-1][j-1]$$ 第一项考虑i位是0，第二项考虑i为是1。先定义一个前缀和$s[i][j]$表示“含有<=j个1”的个数，之后会用的（但是正常的思路肯定是先想到后面的）。 这东西有啥用呢？**看上面样例就知道，第一次超过L个”1”的地方，的下一位一定会进位。** 也就是说问长度为N的第K位，如果$K$比$s[N-1][L]$大，说明首项肯定进位了，就先输出首项的1，然后递归下去求还有$N-1$的长度，第$K-s[N-1][L]$项，如果不进位了就输出0继续递归。 于是之前搞出的DP就派上用场了，就这样不断逼近即可得出答案。 **代码：** ```cpp #include <iostream> using namespace std; int n,l,k; int f[33][33],s[33][33]; //f[i][j] --> L=i,have "1"=j //s[i][j] --> L=i,have "1"<=j void dfs(int n,int m,int k) { if (n<1) return; if (s[n-1][m]<k) cout<<1,dfs(n-1,m-1,k-s[n-1][m]); else cout<<0,dfs(n-1,m,k); } int main() { cin>>n>>l>>k; for (int i=0;i<=n;i++) s[i][0]=f[i][0]=1; for (int i=1;i<=n;i++) s[0][i]=f[0][i]+s[0][i-1]; s[0][1]=0; for (int i=1;i<=n;i++){ for (int j=1;j<=i;j++) //可处理m>n情况 f[i][j]=f[i-1][j]+f[i-1][j-1]; for (int j=1;j<=n;j++) s[i][j]=f[i][j]+s[i][j-1]; } dfs(n,l,k);cout<<endl; } ``` ## [$\color{purple}eg.3:P1560 [USACO5.2]Snail~ Trails$](https://www.luogu.org/problemnew/show/P1560) **题面：** 萨丽·斯内尔（Sally Snail，蜗牛）喜欢在N x N 的棋盘上闲逛（1 < n <= 120）。 她总是从棋盘的左上角出发。棋盘上有空的格子（用“.”来表示）和B 个路障（用“#”来表示）。 萨丽总是垂直（向上或者向下）或水平（向左或者向右）地走。她可以从出发地（总是记作A1 ）向下或者向右走。一旦萨丽选定了一个方向，她就会一直走下去。如果她遇到棋盘边缘或者路障，她就停下来，并且转过90 度。她不可能离开棋盘，或者走进路障当中。并且，萨丽从不跨过她已经经过的格子。当她再也不能走的时候，她就停止散步。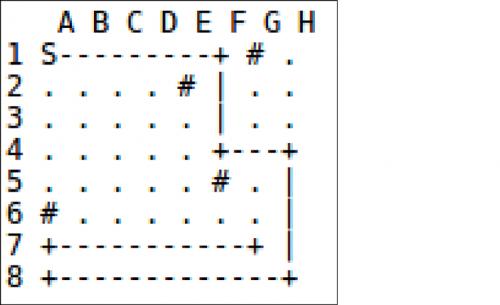 这里是上面的棋盘上的一次散步路线图示：  萨丽向右走，再向下，向右，向下，然后向左，再向上，最后向右走。这时她遇到了一个她已经走过的格子，她就停下来了。但是，如果她在F5 格遇到路障后选择另外一条路——向我们看来是左边的方向转弯，情况就不一样了。 你的任务是计算并输出，如果萨丽聪明地选择她的路线的话，她所能够经过的最多格子数。 **分析：** 这就是USACO比较标准的~~暴力~~深搜题了，虽然思路直白但是细节众多，于是被评到了蓝。。 **直接想法就是每次撞墙时枚举四个方向深搜，直到碰到自己走过的路。走过的路可以开一个地图存，同时再开一个栈来存路径（方便你撤销步数）。** 然后就是一些乱七八糟的小细节： 1. 存图的时候后面数字会超过10，所以要读入一个字符一个整型。。 2. 深搜的时候要判断当前是不是没有移动，直接continue防止死循。 3. 一条路走死可能由于撞墙（或边界）或是走过的路，但往下深搜的时候只能是由于第一种情况。 **代码：** ```cpp #include <iostream> #include <algorithm> #include <stack> using namespace std; int v[200][200],g[200][200]; int ans,n,m; stack<pair<int,int> > q; int dx[4]={1,0,-1,0}; int dy[4]={0,1,0,-1}; char c; int vv; void out(int xx,int yy){ int x=q.top().first,y=q.top().second; while (!q.empty()&&x!=xx||y!=yy)//坐标均不满足！！ { q.pop(); v[x][y]=0; x=q.top().first,y=q.top().second; } //弹出 } bool yuejie(int x,int y) { return (x<=n&&x>0&&y<=n&&y>0); } void dfs(int bx,int by,int sm,int dep) { int now=sm; for (int d=0;d<4;d++) //four direction { int x=bx+dx[d],y=by+dy[d]; while (!g[x][y]&&!v[x][y]&&yuejie(x,y)){ q.push(make_pair(x,y)); v[x][y]=1; now++; x=x+dx[d],y=y+dy[d]; } x=x-dx[d],y=y-dy[d]; if (x==bx&&y==by)continue; //防死循 ans=max(ans,now); if (!v[x+dx[d]][y+dy[d]]) dfs(x,y,now,dep+1); //不因为走过而停止 now=sm; out(bx,by); //还原 } } int main() { cin>>n>>m; for (int i=1;i<=m;i++) { cin>>c>>vv; g[vv][c-'A'+1]=1;//"A11"意会 ,方向 } q.push(make_pair(1,1)); v[1][1]=1; dfs(1,1,1,1); cout<<ans<<endl; } ``` ## [$\color{purple}eg.4:P2747[USACO5.4]Canada~ Tour$](https://www.luogu.org/problemnew/show/P2747) **题面：** 旅行在这家航空公司开放的最西边的城市开始，然后一直自西向东旅行，直到你到达最东边的城市，再由东向西返回，直到你回到开始的城市。除了旅行开始的城市之外，每个城市只能访问一次，因为开始的城市必定要被访问两次（在旅行的开始和结束）。 给出这个航空公司开放的城市的列表，和两两城市之间的直达航线列表。找出能够访问尽可能多的城市的路线，这条路线必须满足上述条件，也就是从列表中的第一个城市开始旅行，访问到列表中最后一个城市之后再返回第一个城市。 **分析：** 这是一道与图论擦边的DP题。这里摘抄一些写题时的思路历程。 首先容易想得到把过去再回来的路径转换成两条不相交过去的路径 不容易想到 设f[i][j]表示起点同时到i,j的最短路径。 容易 得f[i][j]=f[j][i] (3) 得答案应该是f[i][n],i与n连通，这样就可通过i从n返回。 想到既然(3)，那只要转移一维就可以了，f[i][j]=max{f[i][k]}+1，当g[j][k]=1 并不容易 想到如果有香蕉情况出现，则一定会重复经过某点，有f[i][i]答案不为0. 于是我们强制限制j>i搜索，就不会有香蕉啦！ **代码：** ```cpp #include <iostream> #include <map> using namespace std; int n,m,f[1000][1000]; int g[1000][1000],ans=1,num; string s,s1,s2; map<string,int> hash; int main() { cin>>n>>m; for (int i=1;i<=n;i++) cin>>s,hash[s]=++num; for (int i=1;i<=m;i++) { cin>>s1>>s2; int k1=hash[s1],k2=hash[s2]; g[k1][k2]=g[k2][k1]=1; } int ans=1; f[1][1]=1; for (int i=1;i<n;i++) for (int j=i+1;j<=n;j++) for (int k=1;k<j;k++) if (g[j][k]&&f[i][k]) f[i][j]=f[j][i]=max(f[i][j],f[i][k]+1); for (int i=1;i<n;i++) if (g[i][n]) ans=max(ans,f[i][n]); cout<<ans<<endl; } ``` --- 可以注意到，作者所选的题目并不要求代码长度，而是注重在一定的思维性，这也是USACO的题目最考量人的地方。 最后再次建议大家在刷USACO题库的时候也能进行一些取舍，对于无脑爆搜码量大的题目仅要求做到口头AC即可。**（当然，如果您是普及组初学者，爆搜仍是一个重要的技能，还是建议多多练习）** ## $4.~$后续： 关于$USACO$我也只能~~剧透~~说这么多了，更多精彩的题目有待各位OIer们前去发掘，相信这个题库一定不会辜负你们的期望。 除此之外可以分享一下LG管理员[某红包的博客](http://redbag.pw/categories/USACO/training/)，里面对于USACO题库均有较为详细的解释，作者在刷题时也时常参考。 顺便~~厚颜无耻地~~ 再次安利[自己的博客](https://xtzorz.github.io/categories/USACO/)，里面主要是针对一些思维性较高的题目给出的思路分析~~并且自认为写得十分详细~~。 希望大家能通过在USACO上的练习，在OI之路上越走越远。 以上。