浅谈线段树分裂
\text{Part -1} 目录
\text{Part 0} 前言
- Q:有什么数据结构是支持用合并&分裂查询答案信息的呢?
- A:\text{fhq-Treap}
- Q:还有吗?
- A:当然,线段树。
前置芝士:权值线段树、线段树合并
约定:val_x 为节点 x 的权值, ls(x),rs(x) 分别为 x 节点的左儿子、右儿子。
## $\text{Part 1}$ 介绍
线段树分裂,顾名思义就是将线段树分裂开。为了维护线段树合并所维护的可重集,我们需要将权值线段树中前 $k$ 小的位置和其余数分在两颗权值线段树上进行维护。
具体怎么分裂呢?我们来看一张图:
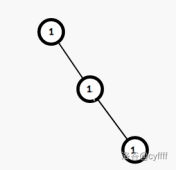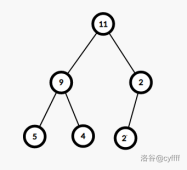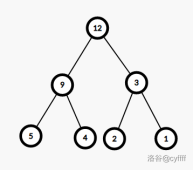
最左边的线段树即可按 $[1,3]$ 和 $[4,4]$ 分裂成右边两颗线段树。
(wtcl 不会画树请谅解)
## $\text{Part 2}$ 实现
怎么实现?
~~我会暴力 $O(n)$!~~
回顾 $\text{Part 0}$,我们将线段树分裂与 $\text{fhq-Treap}$ 对比,现在我们也可以参考 $\text{fhq-Treap}$ 的分裂方法。
考虑函数 $\text{split}(x,y,k)$ 分裂线段树上以 $x$ 为根节点的子树,另一颗线段树为 $y$,其中定义 $v=val_{ls(x)}$。
- $v<k$,左端不需要修改,直接执行 $\text{split}(rs(x),rs(y),k-v)$。
- $v=k$,那么我们发现左子树正好包含前 $k$ 个,于是直接将右子树归给 $y$,即${rs(y)=rs(x),rs(x)=0}$。
- $v>k$,右子树全部大于 $k$,直接归给 $y$,接着递归左子树,执行 $\text{split}(ls(x),ls(y),k)$。
代码很好写,贴一下:
```cpp
inline void split(int x,int &y,ll k){
if(!x) return ;
y=newnode();
ll v=val[son[x][0]];
if(k>v)
split(son[x][1],son[y][1],k-v);
else
swap(son[x][1],son[y][1]);
if(k<v)
split(son[x][0],son[y][0],k);
val[y]=val[x]-k;
val[x]=k;
}
```
我们发现上述三种情况都是每层只递归 $O(1)$ 次,复杂度 $O(\log n)$。
## $\text{Part 3}$ 应用
### 例1 P5494 【模板】线段树分裂
[$\text{Link}$](https://www.luogu.com.cn/problem/P5494)
简化题意:维护一些可重集支持以下操作:
- $\text{cut}(p,x,y)$,将可重集 $p$ 中在 $[x,y]$ 范围中的数移动到一个新的可重集中。
- $\text{copy}(p,t)$,将可重集 $t$ 中的数放入可重集 $p$ 并删除 $t$。
- $\text{insert}(p,x,q)$,向可重集 $p$ 中放入 $x$ 个数字 $q$。
- $\text{query}(p,x,y)$,统计可重集 $p$ 中在 $[x,y]$ 范围中的数的个数。
- $\text{queryk}(p,k)$,查询可重集 $p$ 中第 $k$ 小的数。
每个操作分析一下:
$\text{copy}$ 可以直接 $p=\text{merge}(p,t)$,也就是直接合并线段树。
$\text{insert}$ 可以直接在 $p$ 中单点修改,复杂度 $O(\log n)$。
$\text{query}$,直接区间求和,复杂度 $O(\log n)$。
$\text{queryk}$,求全局第 $k$ 小,复杂度 $O(\log n)$。
$\text{cut}$,考虑将 $[1,x-1],[x,y],[y+1,n]$ 三段 $\text{split}$ 出来,将 $[1,x-1],[y+1,n]\,\,\text{merge}$ 回去即可。
然后是证一下合并的复杂度:
$\text{insert}$ 在线段树中只会新建 $O(1)$ 个叶子,则对于两棵树合并只会造成 $O(\log n)$ 的影响,则总的复杂度是 $O(n\log n)$ 的。
对于 $\text{cut}$ 操作,单次复杂度 $O(\log n)$,如果分裂出来 $x$ 个叶结点,则减少了此后 $O(x\log n)$ 的合并复杂度。如果合并被分裂出来的复杂度增加则需要插入重新补充叶结点,转化为 $\text{insert}$ 的影响。
时间复杂度 $O(n\log n)$。
代码:
```cpp
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=4e5+10;
int n,m;
struct Segment_Tree{
int son[N*20][2],rt[N],cnt,rtc=1;
ll val[N*20];
int pool[N*20],delcnt;
#define ls (son[rt][0])
#define rs (son[rt][1])
inline int newnode(){
return delcnt?pool[delcnt--]:++cnt;
}
inline void del(int rt){
pool[++delcnt]=rt;
ls=rs=val[rt]=0;
}
inline void modify(int &rt,int l,int r,int p,int v){
if(!rt)
rt=newnode();
val[rt]+=v;
if(l==r) return ;
int mid=l+r>>1;
if(p<=mid)
modify(ls,l,mid,p,v);
else
modify(rs,mid+1,r,p,v);
}
inline ll query(int rt,int l,int r,int L,int R){
if(R<l||r<L)
return 0;
if(L<=l&&R>=r)
return val[rt];
int mid=l+r>>1;
return query(ls,l,mid,L,R)+query(rs,mid+1,r,L,R);
}
inline int queryk(int rt,int l,int r,int v){
if(l==r) return l;
int mid=l+r>>1;
if(val[ls]>=v)
return queryk(ls,l,mid,v);
else
return queryk(rs,mid+1,r,v-val[ls]);
}
inline int merge(int a,int b){
if(!a||!b) return a+b;
val[a]+=val[b];
son[a][0]=merge(son[a][0],son[b][0]);
son[a][1]=merge(son[a][1],son[b][1]);
del(b);
return a;
}
inline void split(int x,int &y,ll k){
if(!x) return ;
y=newnode();
ll v=val[son[x][0]];
if(k>v)
split(son[x][1],son[y][1],k-v);
else
swap(son[x][1],son[y][1]);
if(k<v)
split(son[x][0],son[y][0],k);
val[y]=val[x]-k;
val[x]=k;
}
}t;
int main(){
n=read(),m=read();
for(int i=1;i<=n;i++){
int x=read();
t.modify(t.rt[1],1,n,i,x);
}
for(int i=1;i<=m;i++){
int opt=read();
switch(opt){
case 0:{
int x=read(),y=read(),z=read();
ll q1=t.query(t.rt[x],1,n,1,z),q2=t.query(t.rt[x],1,n,y,z);
int a=0;
t.split(t.rt[x],t.rt[++t.rtc],q1-q2);
t.split(t.rt[t.rtc],a,q2);
t.rt[x]=t.merge(t.rt[x],a);
break;
}
case 1:{
int x=read(),y=read();
t.rt[x]=t.merge(t.rt[x],t.rt[y]);
break;
}
case 2:{
int x=read(),y=read(),z=read();
t.modify(t.rt[x],1,n,z,y);
break;
}
case 3:{
int x=read(),y=read(),z=read();
write(t.query(t.rt[x],1,n,y,z));
putc('\n');
break;
}
case 4:{
int x=read(),y=read();
if(t.val[t.rt[x]]<y) write(-1);
else write(t.queryk(t.rt[x],1,n,y));
putc('\n');
break;
}
}
}
flush();
}
```
(我所有代码中的快读快写都删掉了,需要的可以在[$\text{ P7809 }$](https://www.luogu.com.cn/problem/P7809)找到。)
### 例2 P2824 [HEOI2016/TJOI2016]排序
[$\text{Link}$](https://www.luogu.com.cn/problem/P2824)
简化题意:维护一个 $[1,n]$ 的排列,$m$ 次操作,每次操作区间升序或者降序排序,最后求位置 $p$ 上的数。
考虑排序之后合并可以用权值线段树简单合并。
考虑用珂朵莉树维护有序区间,$\text{sort}(l,r,op)$ 可以直接先 $\text{split}'(r+1),\text{split}'(l)$(注意 $\text{split}'$ 是珂朵莉树上的分裂操作),可以将两边的区间 $\text{split}$ 开,再在珂朵莉树中间区间的线段树 $\text{merge}$ 起来即可。
时间复杂度感性分析一下每次分裂多出来 $O(1)$ 级别的区间,总共合并是 $O(n+m)$ 级别的,所以时间复杂度为 $O(n\log n)$($n,m$ 同级)。
```cpp
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=4e5+10;
int n,m;
struct Segment_Tree{
int son[N*20][2],rt[N],cnt,rtc=1;
ll val[N*20];
int pool[N*20],delcnt;
#define ls (son[rt][0])
#define rs (son[rt][1])
inline int newnode(){
return delcnt?pool[delcnt--]:++cnt;
}
inline void del(int rt){
pool[++delcnt]=rt;
ls=rs=val[rt]=0;
}
inline void modify(int &rt,int l,int r,int p){
if(!rt){
rt=newnode();
}
val[rt]=1;
if(l==r) return ;
int mid=l+r>>1;
if(p<=mid) modify(ls,l,mid,p);
else modify(rs,mid+1,r,p);
}
inline int merge(int a,int b){
if(!a||!b) return a+b;
val[a]+=val[b];
son[a][0]=merge(son[a][0],son[b][0]);
son[a][1]=merge(son[a][1],son[b][1]);
del(b);
return a;
}
inline void split(int &x,int y,int v,int p){
if(val[y]==v) return ;
x=newnode();
val[x]=val[y]-v;
val[y]=v;
ll q=val[son[x][0]];
if(v<=val[son[y][p]]){
split(son[x][p],son[y][p],v,p);son[x][!p]=son[y][!p],son[y][!p]=0;
}else{
split(son[x][!p],son[y][!p],v-val[son[y][p]],p);
}
}
inline int query(int rt,int l,int r){
if(l==r) return l;
int mid=l+r>>1;
return ls?query(ls,l,mid):query(rs,mid+1,r);
}
}t;
#define sit set<node>::iterator
struct node{
int l,r;
mutable int v;
node(int L,int R=-1,int V=0):l(L),r(R),v(V){}
friend bool operator<(const node& a,const node &b){
return a.l<b.l;
}
};
set<node>a;
inline sit split(int p){
sit it=a.lower_bound(node(p));
if(it!=a.end()&&it->l==p)
return it;
it--;
int l=it->l,r=it->r,v=it->v;
a.erase(it);
t.split(t.rt[p],t.rt[l],p-l,v);
a.insert(node(l,p-1,v));
return a.insert(node(p,r,v)).first;
}
int main(){
n=read(),m=read();
a.insert(node(n+1,n+1,0));
for(int i=1;i<=n;i++){
t.modify(t.rt[i],0,n,read());
a.insert(node(i,i,0));
}
while(m--){
int opt=read(),l=read(),r=read();
sit R=split(r+1),L=split(l);
L->v=opt;
for(sit i=++L;i!=R;i++)t.merge(t.rt[l],t.rt[i->l]);
a.erase(L,R);
}
int q=read();
split(q+1),split(q);
printf("%d\n",t.query(t.rt[q],0,n));
flush();
}
```
### 例3 CF558E A Simple Task
[$\text{Link}$](https://www.luogu.com.cn/problem/CF558E)
简化题意:维护一个字符串,$m$ 次操作,每次操作区间升序或者降序排序,最后求整个字符串。
我们发现这道题和上一道题基本一样,于是把代码一粘,改几下,发现过不了样例!
于是我们发现上一道题的序列是 $[1,n]$ 的一个排列,这道题的却是有重复的。
怎么处理呢?我们可以强行将 $[1,26]$ 的一个序列“离散化”成 $[1,n]$ 的排列,我们可以用 $\text{pair}$ 进行离散化。
离散化:
```cpp
int d[N],e[N];
pair<int,int>c[N];
for(int i=1;i<=n;i++){
c[i]=make_pair(d[i]=getc()-'a'+1,i);
}
sort(c+1,c+n+1);
for(int i=1;i<=n;i++){
int k=lower_bound(c+1,c+n+1,make_pair(d[i],i))-c;
e[k]=d[i];
}
```
要完整代码可以点 [$\text{Here}$](https://www.luogu.com.cn/paste/ztiz3sk1)。
## $\text{Part 4}$ 后记
写这篇文章加深了我对线段树分裂的理解,因为线段树分裂考到的次数很少,所以没有找到多少题做例子,非常感谢你看到这里,我有些东西写得不够好、不够严谨,或者有其他例题,你们可以帮忙指出,万分感谢!
## $\text{Part 5}$ 参考
[题解 P6012 【【模板】线段树分裂】 - ix35](https://www.luogu.com.cn/blog/ix-35/solution-p6012)
[题解 P2824 【[HEOI2016/TJOI2016]排序】 - 一扶苏一](https://www.luogu.com.cn/blog/fusu2333/solution-p2824)
- $\text{upd 2021.7.4}$:感谢 [dying](https://www.luogu.com.cn/user/85593) 和 [GuidingStar](https://www.luogu.com.cn/user/75840) 指出合并的复杂度证明问题。如果仍错误请继续指出!
- $\text{upd 2021.7.28}$:对部分代码的实现进行修改,更能看了。
- $\text{upd 2021.8.21}$:$\text{fixed a typo}$。
- $\text{upd 2021.8.27}$:$\text{added\&fixed something}$。
- $\text{upd 2021.8.28}$:$\text{fixed something}$。