浅谈斜率优化

参考资料：

https://www.cnblogs.com/Xing-Ling/p/11210179.html

https://blog.csdn.net/mrcrack/article/details/88252442

https://oi-wiki.org/dp/opt/slope/

https://zhuanlan.zhihu.com/p/235343360

绘图：

drawboard PDF

mspaint

前置知识

• 会DP

• 单调队列

• 平面直角坐标系内，两点连线的斜率：\dfrac{y_1 - y_2}{x_1 - x_2}。

• 叉积判断相对位置

Ⅰ 状态转移方程

列出状态转移方程，如果化简为以下的形式：

dp(i) = \min/\max(a(i) \times b(j) + c(i) + d(j)+C)

此时转移时间复杂度 O(n^2)，毒瘤们很不爽。

聪明的前辈们就想：既然状态数是 O(n) 的，可不可以 快速地转移呢？

于是就有了斜率优化DP。

先给出一些约定：

注：没有 a(i)\times b(j) 的 DP 叫做单调队列优化DP，详见往期日报。

Ⅱ 决策点关系

先去掉 \min/\max。

将只有 i ，只有 j 和 i,j 杂糅的项分别合并：

dp(i) = C+(c_1(i) + c_2(i) + ...) + (d_1(j) + d_2(j) + ...) + (a_1(i) + a_2(i) + ...) \times (b_1(j) + b_2(j) + ...)

分析一下：如果存在 j1,j2 使得 j2 优于 j1（\min对应F(j_1)> F(j_2) ，反之为 F(j_1)< F(j_2)，F(j_x) 表示 \min/\max 里在j取j_x时的值），j1,j2 会有什么关系。

\, \boxed{C+(c_1(i) + c_2(i) + ...)} + (d_1(j_1) + d_2(j_1) + ...) + (a_1(i) + a_2(i) + ...) \times (b_1(j_1) + b_2(j_1) + ...) </> \boxed{C+(c_1(i) + c_2(i) + ...)} + (d_1(j_2) + d_2(j_2) + ...) + (a_1(i) + a_2(i) + ...) \times (b_1(j_2) + b_2(j_2) + ...) \, (d_1(j_1) + d_2(j_1) + ...) + (a_1(i) + a_2(i) + ...) \times (b_1(j_1) + b_2(j_1) + ...) </> (d_1(j_2) + d_2(j_2) + ...) + (a_1(i) + a_2(i) + ...) \times (b_1(j_2) + b_2(j_2) + ...)

令：

(d_1(x) + d_2(x) + ...) = Y(x) (a_1(i) + a_2(i) + ...) = k_0 (b_1(x) + b_2(x) + ...) = X(x) \, Y(j_1) + k_0 \times X(j1) </> Y(j_2) + k_0 \times X(j_2) -k_0 </> \dfrac{Y(j_2) - Y(j_1)}{X(j_2) - X(j_1)}

当上述不等式成立时，j_2 优于 j_1。

注：推式子时记得让 X(j_2)>X(j_1)，乱做不等式乘法的小朋友是长不大的qwq

Ⅲ 凸壳

为方便计算，将 k_0 先赋值为 k_0 \times -1

不难发现，上述不等式很像斜率式。

将决策点的 X,Y 丢进平面直角坐标系里。

假设有三个决策点组成点 A,B,C。

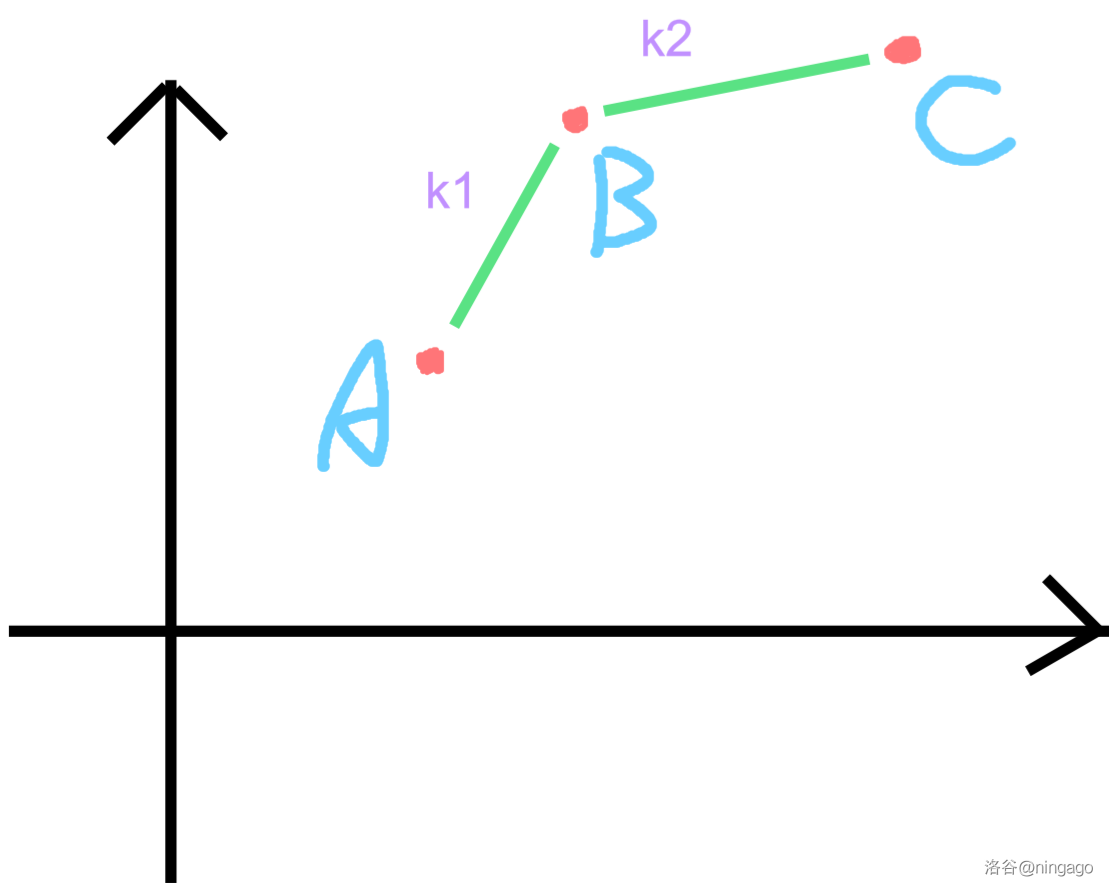
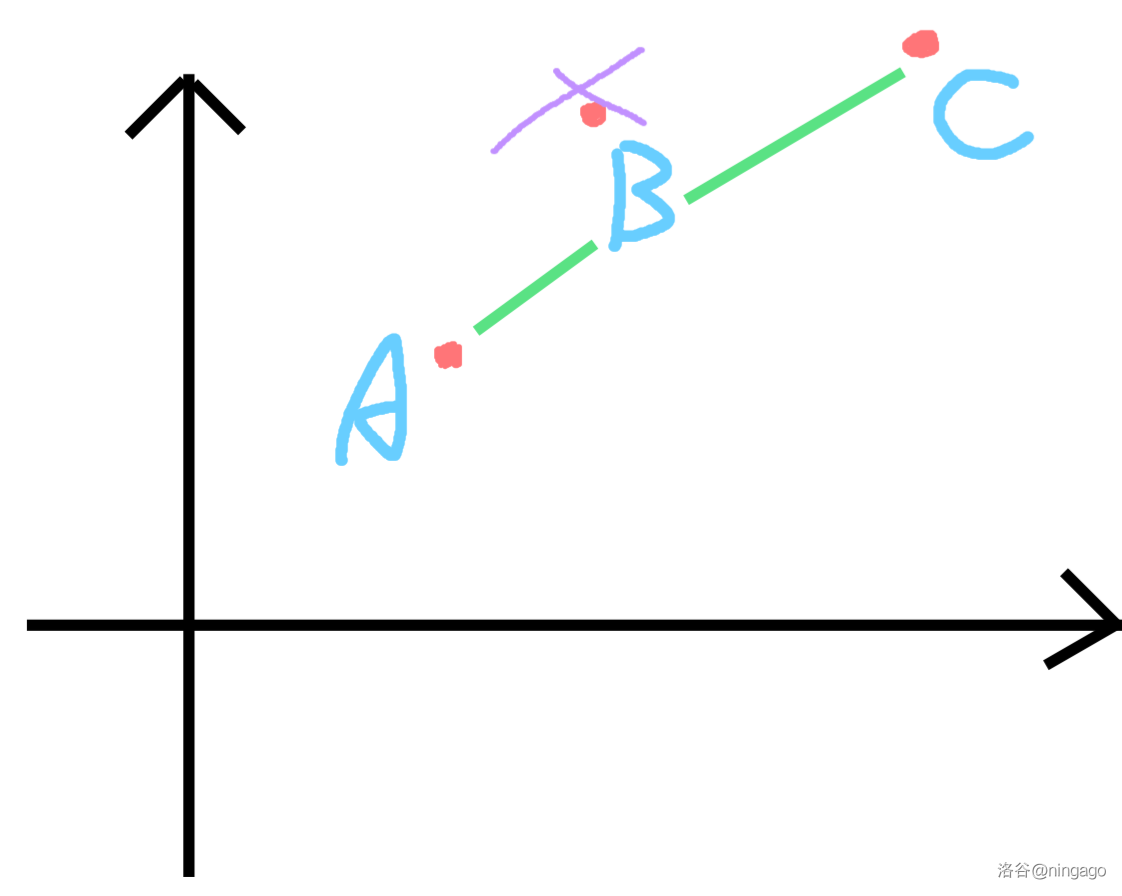
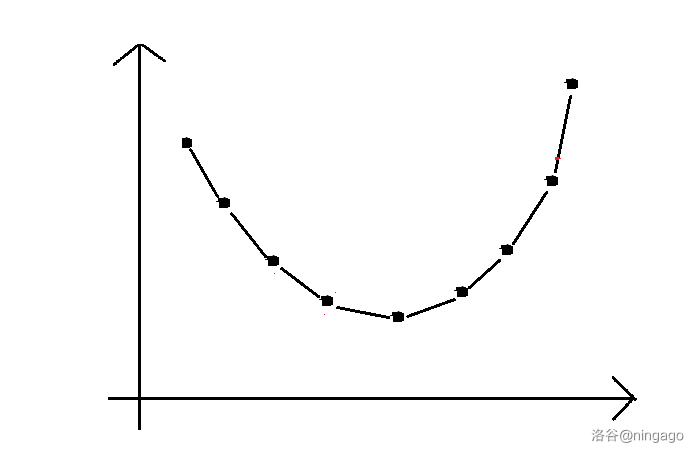
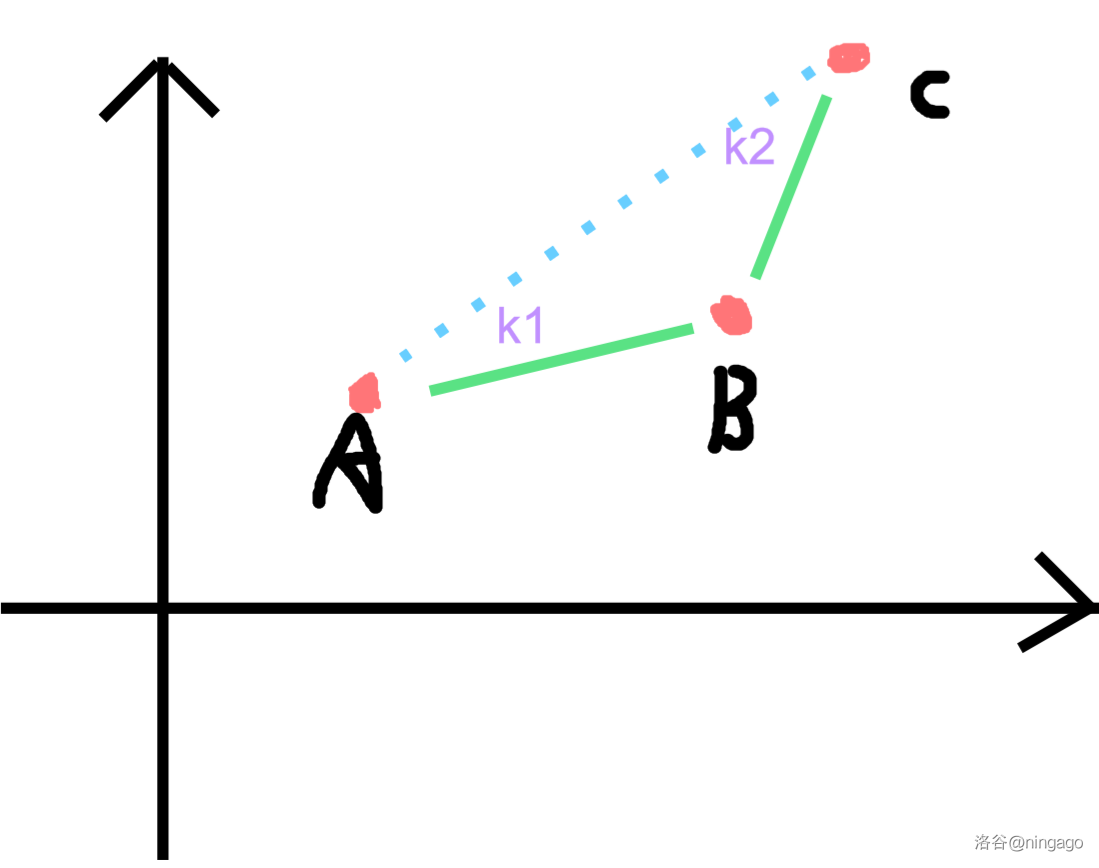
进行如下分类讨论： #### 当 $k_1 > k_2$ 时 如图：  ##### 如果不等式符号为 $>$ : $k_0 > k_1$ 时，$B$ 优于 $A$，反之 $A$ 优于 $B$。 $k_0 > k_2$ 时，$C$ 优于 $B$，反之 $B$ 优于 $C$。 有三种情况： - $k_0 > k_1 > k_2$ ，$C$ 优于 $B$ 优于 $A$。 - $k_1 > k_0 > k_2$ ，$A$ 和 $C$ 优于 $B$。 - $k_1 > k_2 > k_0$ ，$A$ 优于 $B$ 优于 $C$。 综上所述，$B$ 永远不会成为决策点，如下图：  不难发现，可能成为决策点的点形成了一个下凸壳：  ##### 如果不等式符号为 $\le$ : 啥也研究不出…… #### 当 $k_1 < k_2$ 时 思路同上，如图：  ##### 如果不等式符号为 $\le$ : 同理，但形成上凸壳，不再证明。 ##### 如果不等式符号为 $\ge$ : 啥也研究不出…… ## Ⅳ 维护答案 ### 求DP值 下文默认下凸壳。 假设平面上已经维护了一个凸壳，现在需要知道 $dp_i$，假设 $i$ 对应的 $k_0$ 所构成的斜率是图中红线。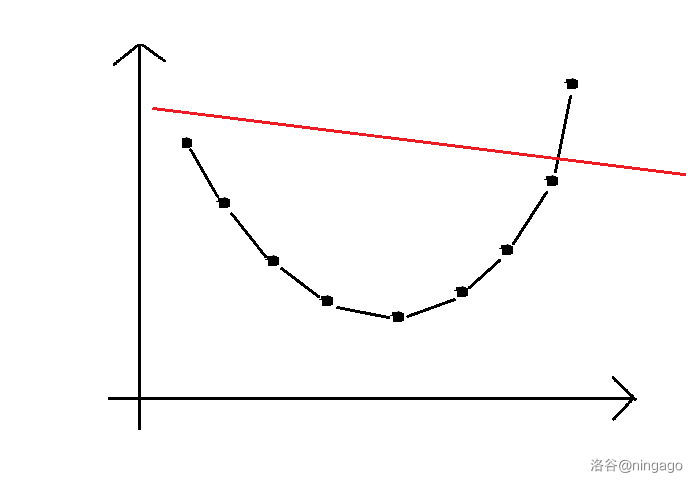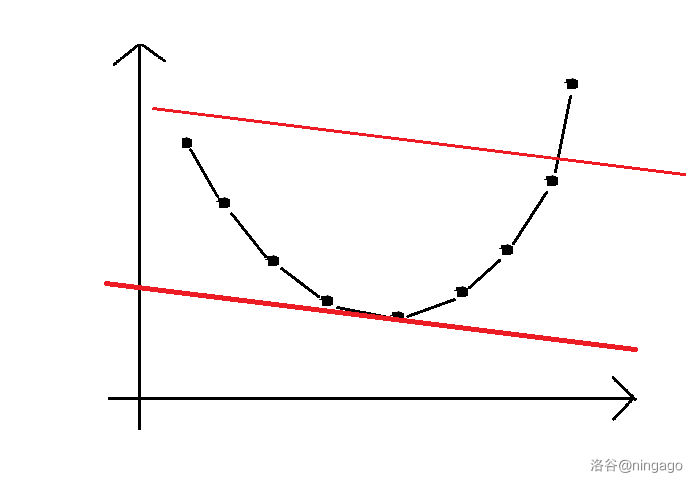  用眼睛可以看出五号点就是最优决策点：  设维护出凸包的点集为 $\{(x_i,y_i)\}(i\in [1,m])$，$m$ 为集合大小。 由于凸壳的性质（默认下凸），这些点满足：$\dfrac{y_i-y_{i+1}}{x_i-x_{i+1}}<\dfrac{y_j-y_{j+1}}{x_j-x_{j+1}}$，其中 $i<j,i\text{ 和 }j\in [1,m)$，通俗地讲就是前面的斜率小于后面的斜率。 注意到决策点的优劣满足传递性：即如果 $A$ 优于 $B\ (A<B)$，那么 $\forall B$ 优于 $C (B<C)$，$A$ 优于 $C$。 这启发我们使用二分，$O(\log n)$ 得到答案。 初始化将 $l,r$ 设为 $1,m-1$（$m-1$ 是因为 $m$ 个点连 $m-1$ 条线），二分的答案先赋为一个不存在的值，并计算出 $k_0$： ```cpp int l = 1,r = m - 1,j = -0x3f3f3f3f; k0 = /**/; ``` 如果此时 $mid$ 优于 $mid+1$，就把答案 $j$ 更新为 $mid$，移动右端点。反之移动左端点 ```cpp while(l <= r) { ll mid = l + r >> 1; // > if(k0 * (X(mid + 1) - X(mid)) < (Y(mid + 1) - Y(mid))) r = mid - 1,j = mid; else l = mid + 1; } ``` 二分结束后，如果 $j=\texttt{-0x3f3f3f3f}$，那么说明切点在 $[1,m-1]$ 之外的那个点上，也就是 $m$ 号点，此时将 $j$ 赋值为 $m$。 ```cpp if(j == -0x3f3f3f3f) j = m; ``` 然后根据转移方程填充 $dp_i$ 即可。 注：维护的数据结构不同，需要适当地改变二分模板。 ### 加点 也就是把一个点（$(X_i,Y_i)$）塞入凸包里 动态凸包问题可以使用平衡树或CDQ分治、李超树解决。 **不会平衡树的萌新可以跳过这一节，因为 $70\%$ 的题都用不上** 李超树是不可能的，这辈子都不可能的（） 离线是不可能的，这辈子都不可能的（） 这里介绍平衡树做法： （下文默认下凸） ① 判断点是否在凸壳内部 如图所示：如果以该点为观测点，该点的前驱在后继的顺时针方向，那么就说明在凸壳内部（上凸对应逆时针），反之就在外部。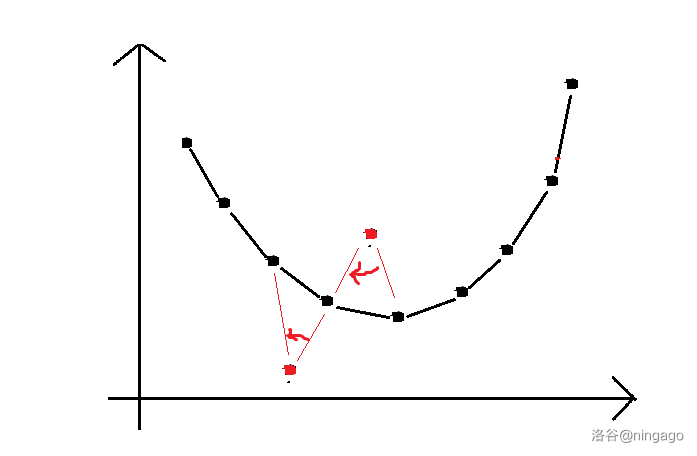 （前驱，后继指 $X$ 值小于/大于此点的最大/最小的点）  特殊地，没有前驱或后继相当于在凸包外部。 为方便理解且每个人使用平衡树不同，这里给出 `set` 实现的代码，读者在练习时可将模板转移到自己擅长的平衡树上。 定义结构体存点： ```cpp struct node { int x,y; node operator - (const node &B)const { return (node){x - B.x,y - B.y}; } int operator * (const node &B)const { return x * B.y - y * B.x; } bool operator < (const node &B)const { return (x != B.x) ? x < B.x : y > B.y; } }; multiset<node>s; #define sit multiset<node>::iterator ``` 顺逆时针使用叉积判断即可 ```cpp bool inside(sit p) { if(p == s.begin()) return 0; sit nx = next(p); if(nx == s.end()) return 0; sit pre = prev(p); return ((*pre - *p) * (*nx - *p)) >= 0; // <= } ``` ②加点 显然，如果该点在凸壳内部，就无需加入凸壳（永远不可能成为决策点） ```cpp void ins(node t) { sit p = s.insert(t); if(inside(p)) { s.erase(p); return; } ... ``` 否则先将点加入凸壳，再`while`判断前驱后继在不在新凸壳里，要不要删去。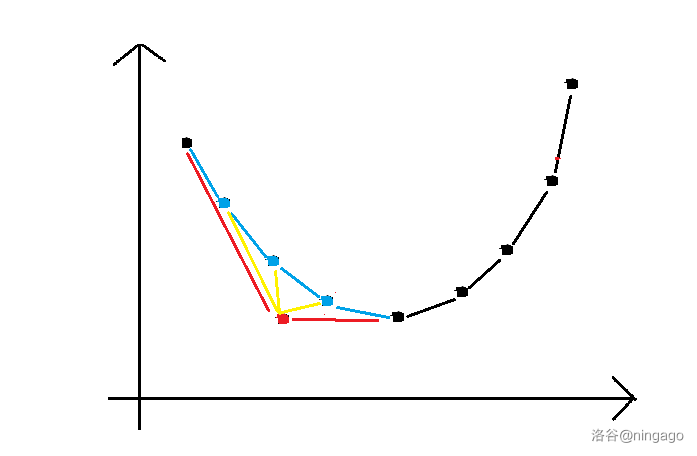  ```cpp while(p != s.begin() && inside(prev(p))) s.erase(prev(p)); while(next(p) != s.end() && inside(next(p)) s.erase(next(p)); } ``` ## Ⅴ 特殊性 由于一些特殊的单调性，大部分题目都用不着平衡树和二分，可以特殊解决： ### $k_0

如果 k_0 随着 X_i 的递增单调（下凸对应递增，上凸对应递减），说明决策点随着 X_i 的增大而增大，就说明如果决策点 j 在 dp_p(p<i) 的答案计算时被淘汰了，那么就再也成为不了决策点了。

此时可以使用一个单调队列来维护，避免了二分的过程。

ll k0 = /**/;

先计算出 i 点的 k_0。

//                  <=
while(hh < tt && k0 >= K(q[hh],q[hh + 1]))
    hh++;
ll j = q[hh];
dp[i] = /**/;

用暴力的方法找到决策点，不同于普通暴力的是不符合条件的点直接被弹出队列。

由于每个节点只会被插入和删除一次，统计答案的时间复杂度是单次均摊 O(1) 的

X_i

如果 X_i 是单调的，意味着每次插入点都是在凸包后面（如果是前面也是可行的，但似乎没见过这样的魔怔题），如图（红点为新加点，蓝点为被删点）：

这样使得在平衡树中，每次插入点都是在平衡树尾部，也就是说没有必要使用平衡树了，使用栈维护即可（栈可嵌入到 k_0 单调的单调队列里去）。

由单调性可知，加点 i 一定在原凸壳外部，无需inside 函数判断。

//                                  <=
while(hh < tt && K(q[tt - 1],q[tt]) >= K(q[tt - 1],i))
    tt--;
q[++tt] = i;

把不符合凸性的点直接出队，最后将 i 入队。

在凸包最后加点。

加点的时间复杂度加速为单次均摊 O(1)

Ⅵ 模板Code

二分（X_i 单调，k_0 不单调）：

#include <cstdio>

#define N 300010
#define ll long long

ll q[N],hh = 1,tt = 1;

inline ll Y(ll x)
{
    return /**/;
}

inline ll X(ll x)
{
    return /**/;
}

int main()
{
    /*输入*/
    for(ll i = 1;i <= n;i++)
    {
        ll k0 = /**/;
        ll l = hh,r = tt - 1,j = -0x3f3f3f3f;
        while(l <= r)
        {
            ll mid = l + r >> 1;
            //                                  >=
            if(k0 * (X(q[mid + 1]) - X(q[mid])) <= (Y(q[mid + 1]) - Y(q[mid])))
                r = mid - 1,j = q[mid];
            else
                l = mid + 1;
        }
        if(j == -0x3f3f3f3f)
            j = q[tt];
        dp[i] = /**/;
        while(hh < tt && (Y(i) - Y(q[tt])) * (X(q[tt]) - X(q[tt - 1])) <= (Y(q[tt]) - Y(q[tt - 1])) * (X(i) - X(q[tt])))
        //                                                             >=
            tt--;
        q[++tt] = i;
    }
    /*输出*/
    return 0;
}

都单调：

#include <cstdio>
#include <iostream>
#include <cstring>

#define ll long long
#define N 50005
using namespace std;
ll n,dp[N],q[N];
inline ll X(ll x)
{
    return /**/;
}

inline ll Y(ll x)
{
    return /**/;
}

inline double K(ll j1,ll j2)
{
    double res = (double)(Y(j2) - Y(j1)) / (double)(X(j2) - X(j1));
    return res;
}

int main()
{
    /*输入*/
    ll hh = 1,tt = 1;
    for(ll i = 1;i <= n;i++)
    {
        ll k0 = /**/;
        while(hh < tt && k0 >= K(q[hh],q[hh + 1]))
        //                  <=
            hh++;
        ll j = q[hh];
        dp[i] = /**/;
        while(hh < tt && K(q[tt - 1],q[tt]) >= K(q[tt - 1],i))
        //                                  <=
            tt--;
        q[++tt] = i;
    }
    /*输出*/
    return 0;
}

Ⅶ 注意事项

ⅰ 有时将除法写成乘法以保证精度；

ⅱ 有时，dp 数组为多维，也就是 dp[i][j] 等，此时可考虑将 i,j 都枚举，再找 j 的决策点；

ⅲ 注意初值，从 0 号点（也就是从头）转移有时要提前在凸壳里加入 \{0,0\} 等初值

ⅳ 对于一些题目，X(j2) - X(j1) = 0，此时做除法直接爆炸，建议写成 X(j2) - X(j1) == 0 ? eps : X(j2) - X(j1)，eps 为极小值，例如 1e-6；

ⅴ按照题目的取等条件，注意是否要维护严格凸的凸壳，例如下面这样（共线）

ⅵ 加点和统计答案是两个不同的事件，不是所有题目都统计完就加点

ⅶ 凸包维护有时不止一个，具体问题具体分析

Ⅷ 例题

P3628 [APIO2010] 特别行动队

以 dp_i 表示以 i 为某一队的结尾，最大的价值。

显然可以枚举上一队的结尾 j(j\in[0,i-1])，则转移方程：

dp_i = \max_{j<i}\{dp_j+a(s_i-s_j)^2+b(s_i-s_j)+c\} 拆开平方，提取常数： $$dp_i = \max_{j<i}\{dp_j-2as_is_j+as_j^2-bs_j\}+bs_i+c+as_i^2$$ 若 $j_2$ 优于 $j_1$，则 $$dp_{j1}-2as_is_{j1}+as_{j1}^2-bs_{j1}<dp_{j2}-2as_is_{j2}+as_{j2}^2-bs_{j2}$$ $$2as_i(s_{j2}-s_{j1})<(dp_{j2}+as_{j2}^2-bs_{j2})-(dp_{j1}+as_{j1}^2-bs_{j1})$$ $$2as_i<\dfrac{(dp_{j2}+as_{j2}^2-bs_{j2})-(dp_{j1}+as_{j1}^2-bs_{j1})}{(s_{j2}-s_{j1})}$$ $(s_{j2}>s_{j1})

令 X_x = s_x，Y_x=dp_x+as_x^2-b_x，k_0=2as_i

k0<\dfrac{Y(j2)-Y(j1)}{X(j2)-X(j1)}

维护上凸包即可

#include <cstdio>

#define N 1000010
#define ll long long
inline ll max(ll x,ll y){return x < y ? y : x;}
inline ll min(ll x,ll y){return x < y ? x : y;}
#define pow2(x) ((x) * (x))

ll n,a,b,c;
ll s[N],dp[N];
inline ll Y(ll x)
{
    return dp[x] + a * pow2(s[x]) - b * s[x];
}

inline ll X(ll x)
{
    return s[x];
}

inline double k(ll x,ll y)
{
    return (double)(Y(x) - Y(y)) / (double)(X(x) - X(y) == 0 ? 0.00001 : X(x) - X(y));
}
ll q[N],hh = 1,tt = 1;
int main()
{
    scanf("%lld%lld%lld%lld",&n,&a,&b,&c);
    for(ll i = 1,x;i <= n;i++)
    {
        scanf("%lld",&x);
        s[i] = s[i - 1] + x;
    }
    for(ll i = 1;i <= n;i++)
    {
        ll k0 = 2 * a * s[i];
        while(hh < tt && k0 <= k(q[hh],q[hh + 1]))
            hh++;
        ll j = q[hh];
        ll S = s[i] - s[j];
        dp[i] = dp[j] + a * pow2(S) + b * S + c;
        while(hh < tt && k(q[tt],q[tt - 1]) <= k(i,q[tt - 1]))
            tt--;
        q[++tt] = i;
    }
    printf("%lld\n",dp[n]);
    return 0;
}

Ⅸ 练习

[HNOI2008]玩具装箱 入门（单调队列）；

[NOIP2018 普及组] 摆渡车 入门（单调队列）；

任务安排 入门（单调队列） / [SDOI2012]任务安排 （单调队列上二分）；

[SDOI2016]征途 二维DP，细节较多（单调队列）。

[CEOI2017] Building Bridges （平衡树）；

[NOI2019] 回家路线 拆事件/多个凸包（单调队列）

End.

笔者垃圾，错误请在评论区指出qwq

Ⅹ 评论区问题解答