一些基本的记号和约定(并不包括本文的所有):
$n(G)=|V|$,$e(G)=|E|$,$f(G)$ 表示可平面图的平面嵌入的面数。
$G-u$ 表示 $G$ 去掉点 $u$ 得到的图,$G-e$ 表示 $G$ 去掉边 $e$ 得到的图。
$\delta (G)$ 表示图 $G$ 节点的最小度,$\Delta(G)$ 表示图 $G$ 的最大度。
诱导子图是一个图中保留一部分节点和两端都在这些节点中的边的子图。生成子图指保留全部节点和部分边的子图。
$K_n$ 表示大小为 $n$ 的完全图。
$\omega(G)$ 表示图 $G$ 的最大团的大小。最大团就是一个图中最大的是完全图的诱导子图。
$N(V)$ 表示与节点 $v$ 相邻的所有节点组成的集合,$d(v)$ 表示 $v$ 的度。
$\chi(G)$ 表示给图 $G$ 的点染色使相邻节点颜色不同的最小颜色数目。
$\chi(G,k)$ 既可以表示 $G$ 的色多项式,也可以表示用 $k$ 种颜色给 $G$ 染色的方案。其他意义在以后会提。
为了方便,颜色编号从 $1$ 开始,是正整数。
本文所讨论的所有图都是简单连通图。
# 一些显然或较为简单的定理:
**定理一**:$\chi(G)\le \Delta(G)+1
事实上,不等式中的等号在 G 是完全图或者有奇数个节点的环时才成立(连通图),这就是 Brooks 定理。证明有点复杂,这里就不放上来了抄书没有意思。
定理二:\chi(K_n)=n
定理二的推论: \chi(G) \ge \omega(G)。
前面的内容都很平凡。
定理三:\chi(G) \le 1+\max\limits_{H\subseteq G} \delta(H)
证明:显然,在图 G 中,不断去掉一条边使 G 的色数减一或不变。于是可以找到这样一个连通生成子图 H 使 \chi(H)=\chi(G) 且在 H 中去掉任意一条边后色数刚好减一。于是对于任意一个节点 u,\chi(H-u)=\chi(G)-1。先在 H-x 用 \chi(G)-1 种颜色染色,若 d(u)\le \chi(G)-2,则 N(u) 中最多出现 \chi(G)-2 种颜色,所以用没有出现过的那个颜色就得到 \chi(H)=\chi(G)-1,矛盾。所以 d(u) \ge \chi(G)-1,\delta(H)\ge\chi(G)-1=\chi(H)-1。
现在,找到这样的 H 就可以得到 \chi(G)=\chi(H) \le \delta(H)+1 \le 1+\max\limits_{H\subseteq G} \delta(H)
在 OI 中,巧妙运用这些定理也许可以用来骗分(
染色计数:
图 G 的色多项式 \chi(G,k)=f(k) 就是一个多项式使得对于任意的 k,G 用小于等于 k 种颜色染色的方案数是 f(k) 。
先来看一些结构较为简单的图的色多项式:
对于有 n 个节点的树,\chi(T,k)=k(k-1)^{n-1}。
对于树 $T$,从根节点往下染色就会发现除了根节点,所有的节点都有 $k-1$ 中选择而根有 $k$ 种。对于完全图,涂上 $i$ 个节点的颜色后下一个节点就只有 $k-i$ 种选择了。每次乘上每个节点的可能的选择就得到了那两个式子。
大多数时候色多项式不容易求出,下面给出一些简化方法:
**定理四**:$\chi(G,k)=\sum\limits^{|V(G)|}_{i=1} f(G,i)A^k_i$,其中 $f(G,i)$ 表示将 $G$ 划分为 $i$ 个非空独立集的方案数。
**证明**:对于每个染色,其中出现的每一种颜色中的节点就可以看作非空独立集。枚举颜色的个数,$f(G,i)$ 就表示正好用 $i$ 种给 $G$ 上色的方案数。而有 $k$ 种颜色的话,从中选 $i$ 种颜色的方案就是 $A^k_i$。相乘就可以得到这个定理。
这个定理在 $k$ 远远大于 $G$ 的点数时可以较为简便的计算染色方案数。
定理四的推论:色多项式 $\chi(G,k)$ 是一个 $|V(G)|$ 次多项式,且首项系数为 $1$ ,第二项系数为 $-|E(G)|$。
用这个定理来计算色多项式的时间复杂度依然过高并且容易使运算途中出现过大的数。所以我们需要一个新的方法去计算它。
**定理五**:对于任意$e\in E(G)$ 有 $ \chi(G,k)=\chi(G-e,k)-\chi(G\cdot e,k)$。这里 $G \cdot e$ 表示在 $G$ 中去掉 $G$ 的端点 $x$,$y$并加入一个新节点 $z$,让 $z$ 和 $N(x)\cup N(y)$ 中不为 $x,y$ 的节点连边。得到的新图就是 $G\cdot e$。(其实就是收缩边 $e$。)
**证明**:考虑 $G-e$ 的所有染色方案,显然,在其中减去 $e$ 的两端的节点颜色相同但其他相邻节点颜色都不同的方案就是 $G$ 的染色方案。这种情况下,收缩边就得到 $G \cdot e$ 的一个合法方案。同样,$G \cdot e$ 中把节点拆开来,也可以得到这样( $e$ 的两端的节点颜色相同但其他相邻节点颜色都不同)的一个染色方案。
直接这个方法计算图的色多项式的时间复杂度很容易得出是 $O(2^{|E|}(|V|+|E|)$ 的。并且中途还会因为收缩边时出现重边而降低时间。不过代码十分复杂,于是我们有下面的定理:
**定理六**:$\chi(G,k)=\sum \limits_{S \subseteq E} (-1)^{|s|}k^{c(G(S))}
$,其中 $G(S)$ 表示只保留 $S$ 中的边得到的生成子图,$c(G(S))$ 表示这个图的分量个数。
证明略,读者自证不难(
其实把 $S$ 中的边当做定理五中收缩掉的边就行了。
这个式子不仅用代码直接计算方便,还可以用于计算特殊图的色多项式。
求色多项式的代码:
```cpp
#include<bits/stdc++.h>
using namespace std;
int n,m,u,v,f[1005],vis[1005],cnt;
struct node{
int to,p;
};
vector<node>ve[1005];
int q(int num){
int res=0;
while(num){
res+=(num&1);
num>>=1;
}
return res;
}
void dfs(int now,int opt){
vis[now]=1;
for(int i=0;i<ve[now].size();i++){
if(!((1<<ve[now][i].p)&opt))continue;
int y=ve[now][i].to;
if(vis[y])continue;
dfs(y,opt);
}
}
signed main() {
cin>>n>>m;
for(int i=0;i<m;i++){
cin>>u>>v;
ve[u].push_back((node){
v,i
});
ve[v].push_back((node){
u,i
});
}
for(int i=0;i<(1<<m);i++){
for(int j=1;j<=n;j++)vis[j]=0;
cnt=0;
for(int j=1;j<=n;j++)if(!vis[j])dfs(j,i),cnt++;
f[cnt]+=(q(i)&1)?-1:1;
}
for(int i=n;i>=0;i--)cout<<f[i]<<' ';
cout<<endl;
}
```
对于一个 $n$ 个节点的环 $C_n$,有
$$\chi(C_n,k)=\sum \limits_{S \subseteq E} (-1)^{|s|}k^{c(G(S))}$$
$$=\sum\limits_{i=0}^{n-1}(-1)^i\tbinom{n}{i}k^{n-i}+(-1)^{n}k$$
$$=\sum\limits_{i=0}^{n}(-1)^i\tbinom{n}{i}k^{n-i}+(-1)^{n}k-(-1)^n$$
$$=(k-1)^n+(-1)^{n}k-(-1)^n$$
$$=(k-1)^n+(-1)^{n}(k-1)$$
(第二个式子里直接按 $|S|$ 的大小分类讨论了一下,然后上二项式定理,下面也是一样的思路。)
对与 $n$ 个节点,环长为 $a$ 的基环树 $T$,有
$$\chi(T,k)=\sum \limits_{S \subseteq E} (-1)^{|s|}k^{c(G(S))}$$
$$=\sum\limits_{i=0}^{n-a}\sum\limits_{j=0}^{a-1} (-1)^{i+j}\tbinom{n-a}{i}\tbinom{a}{j}k^{n-i-j}+\sum\limits_{i=0}^{n-a}(-1)^{i+a}\tbinom{n-a}{i}k^{n-i-a+1}$$
$$=k^n(\sum\limits_{i=0}^{n-a}(-1)^i\tbinom{n-a}{i}k^{-i})(\sum\limits_{j=0}^{a-1} (-1)^{j}\tbinom{a}{j}k^{-j})+k(-1)^a\sum\limits_{i=0}^{n-a}(-1)^{i}\tbinom{n-a}{i}k^{n-i-a}$$
$$=(\sum\limits_{i=0}^{n-a}(-1)^i\tbinom{n-a}{i}k^{n-a-i})(\sum\limits_{j=0}^{a-1} (-1)^{j}\tbinom{a}{j}k^{a-j})+(-1)^ak(k-1)^{n-a}$$
$$=(k-1)^{n-a}((k-1)^{a}-(-1)^a)+(-1)^ak(k-1)^{n-a}$$
$$=(k-1)^{n}-(-1)^a(k-1)^{n-a}+(-1)^ak(k-1)^{n-a}$$
一道例题(JSOI2020冬令营的,已取得出题老师同意):
```
天际的光,依旧亮着。 好像来自遥远的地方,或许永远也触及不到吧。 但这已经是夜了。 那么为什么世界还是一片白色? 或许,这就是白夜吧。 白夜,实际上是不眠的人呢。 他们眼中的世界,真的是纯白的呢。 纯白的世界,真的好无聊呢…… 那不如……
白夜中的世界可以看作一棵 n 个点的树。
你现在觉得这个白色的世界过于单调,因此想用颜料给树上的每个点染上颜色,相邻两 个点不能染成同色。
如果仅仅染上颜色,也没什么意思,树的形态也要变一变对吧。
有 q 次询问,每次询问形如 u v k,表示假设在(u,v)之间连一条边,然后询问使用不 超过 k 种颜色将整棵基环树染色的方案数。
(如果存在自环,那么方案数为 0)
注意:每次询问是独立的,即不会真正修改树的形态。
```
显然,用刚才的式子带进去,再套上 LCA 求环长即可。代码略,因为这篇文章基本上不是讲 OI 的。
你也许以为这一节讲完了,但我还有个奇妙的玩意要讲。
**定理七**:一个图 $G$ 的无环定向数目为 $(-1)^{n(G)}\chi(G,-1)
对 e(G) 使用归纳大法,当 e(G)=0 时显然。
若 e(G) \ge1,那么由归纳法,(-1)^{n(G)}\chi(G-e,-1) 和 (-1)^{n(G)-1}\chi(G \cdot e,-1) 分别表示 G-e 和 G \cdot e 的无环定向个数。而 \chi(G,-1)=\chi(G-e,-1)-\chi(G \cdot e,-1),故 (-1)^{n(G)}\chi(G,-1)=(-1)^{n(G)}\chi(G-e,-1)+(-1)^{n(G)-1}\chi(G \cdot e,-1)。由此我们可以得出,证明这个定理只要证明 G 的无环定向数量等于 G-e 的无环定向数目加上 G \cdot e 的无环定向数目。
设 e 连接的是 u 和 v。对于 G-e 的每个无环定向,显然我们做一次拓扑排序,按拓扑序小的往大的连,就可以得到 G 的一个无环定向。
由上面的结论可得 $G$ 的无环定向数目 $=$ $G-e$ 的无环定向数目 $+ G-e$ 中不存在 $u$ 到 $v$ 或 $v$ 到 $u$ 路径的无环定向数目$=$ $G-e$ 的无环定向数目 $+ G \cdot e$ 的定向数目。定理得证。
# 特殊图的染色:
## 可平面图
**定理八:可平面图的色数最多为 $6$**
首先平面图的欧拉公式 $n(G)+f(G)-e(G)=2$ 这里就不证明了。收缩边归纳一下就好。显然,对于任意平面一个图 $G$,如果有 $n(G) \ge 4$ 且 $G$ 连通的话,则对于每个面,都至少由 $3$ 条边围成,而一条边最多左右各一个面。于是 $2e(G) \ge 3f(G)$。带入,$2=n(G)+f(G)-e(G)\le n(G)-\frac{1}{3}e(G)$,所以 $e(G)\le 3n(G)-6$。
这样就得到了所有点的度数的和 $2e(G)\le 6n-12$,所以必有一点度小于 $6$。于是就可以归纳了。
对于 $n(G)\le6$ 的图,定理成立。
对于图 $G$,现在假定所有点数小于 $n(G)$ 的可平面图可以用六种颜色染色。找到 $G$ 里的一个度小于 $6$ 的点。去掉这个点,得到一个新的可平面图。这个点取与它相邻的点中没有出现过的第 $6$ 种颜色即可。由归纳假设,$G$ 有一个用六种颜色染色的方案。
**定理九:可平面图的色数最多为 $5$**
下文颜色用 $12345$ 表示,归纳法中待染色的节点用 $0$ 表示,与 $0$ 号节点相邻的节点用它的颜色编号表示
我们在上个定理的基础上继续推导。在做归纳法的时候,假设被去掉的点的相邻的五个节点只有颜色互不相同的染色方案,也就是说去掉的点只能用第 $6$ 种颜色表示,如下图:
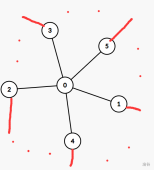
设 $G_{i,j}$ 为所有颜色为 $i$ 或 $j$ 的节点的诱导子图。如果 $1$ 号节点和 $3$ 号节点不在 $G_{1,3}$ 的同一分量中的话,那么在 $3$ 所在的分量中把颜色为 $1$ 的颜色换成 $3$ ,颜色为 $3$ 的颜色换成 $1$,那么 $3$ 号点的颜色就变成了 $1$ ,节点 $0$ 就可以用 $3$ 染色,与假设矛盾。
如果 $1$ 号节点和 $3$ 号节点在 $G_{1,3}$ 的同一分量中如下图(旁边标的数字表示颜色编号):
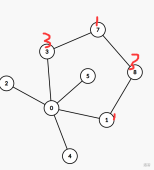
那么容易得到 $5$ 号节点和 $2$ 号节点不在 $G_{2,5}$ 的同一分量中(被 $G_{1,3}$ 隔开了),所以 $5$ 号节点可以用 $2$ 染色。
当然,这种情况也是一样的:
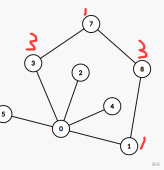
## 完美图
阅读如下内容时建议先了解 [弦图OI-wiki](https://oi-wiki.org/graph/chord/),其中提到的记号会在接下来直接使用。
**定义:** 图 $G$ 是 $\alpha$-完美的当且仅当对于 $G$ 的任意诱导子图 $H$,有 $\theta(H)=\alpha(H)$,图 $G$ 是 $\gamma$-完美的当且仅当对于 $G$ 的任意诱导子图 $H$,有 $\chi(H)=\omega(H)$。
令 $\overline{G}$ 为去掉 $G$ 中所有边并连接上所有 $G$ 中没有的边得到的图 ($G$ 的补图),那么显然图 $G$ 是 $\alpha$-完美的和图 $\overline{G}$ 是 $\gamma$-完美的等价。
**定义:** 在图 $G$ 中添加一个顶点 $u'$ 使得 $N(u')=N(u)$,那么得到的新图叫做对 $G$ 中顶点 $u$ 的顶点复制,记为 $G\circ u$。给定非负整数向量 $h=(h_1,h_2,\dots,h_n)$,定义图 $H=G\circ h$。$H$ 的顶点包含了 $G$ 中顶点 $x_i$ 的 $h_i$ 个复制。而$x_i$ 和 $x_j$ 的复制之间有边当且仅当 $x_i$ 和 $x_j$ 之间有边。从 $G$ 得到这个新图也叫多重顶点复制。
由定义易知 $G\circ(1,1,\dots,1)$ 就和 $G$ 同构而 $G\circ (1,1,\dots,2,\dots,1)$ 就是 $G$ 的一个定点复制。
**定理十: 多重顶点复制保持 $\gamma-$ 完美和 $\alpha-$ 完美。**
**证明**:显然 $G\circ h$ 可以由 $G$ 的一个诱导子图进行连续的顶点复制得到,所以只要证明定点复制保持两个完美性即可。
进一步的,因为 $G\circ u$ 的每个诱导子图都是 $G$ 的诱导子图或$G$ 的诱导子图的一个定点复制,所以证明 $\theta(G\circ u)= \alpha(G\circ u)$ 和 $\chi(G\circ u)=\omega(G\circ u)$ 就行了。
如果 $G$ 是 $\alpha-$ 完美的,那么在 $G\circ u$ 中,给 $u'$ 染上和 $u$ 一样的颜色即可,这样就得到了 $\chi(G)=\chi(G
\circ u)$。而 $u$ 和 $u'$ 不会在同一个团里,故 $\omega(G)=\omega(G\circ u)$。
如果 $G$ 是 $\gamma-$ 完美的,那么对 $u$ 分类讨论。
若 $u$ 在 $G$ 的一个最大独立集内,那么 $u'$ 加上 $G$ 的这个最大独立集得到 $\alpha(G\circ u)=\alpha(G)+1$,此时用 $G$ 的最小团覆盖和一个大小为 $1$ 的团覆盖 $u'$ 即得 $\theta(G\circ u)\le \theta(G)+1$。而显然 $\theta(G\circ u)\ge \alpha(G\circ u)$,故 $\theta(G\circ u)= \theta(G)+1=\alpha(G\circ u)$。
若 $u$ 不在 $G$ 的任何一个最大独立集中,那么显然 $\alpha(G)=\alpha(G\circ u)$。此时在 $G$ 的最小团覆盖中,找到一个覆盖 $u$ 的团 $Q$。由于 $\theta(G)=\alpha(G)$,$Q$ 与 $G$ 的一个最大独立集相交。由于 $u$ 不在任意一个最大独立集中,所以 $Q'=Q-u$ 也和任意一个最大独立集相交。于是 $\theta(G-Q')=\alpha(G)-1$。由 $G-Q'$ 的完美性,
theta(G-Q')=\alpha(G-Q')。故将 Q' 和 u' 得到的 G\circ u 的诱导子图作为一个团覆盖加入 G-Q' 的团覆盖得到 \theta(G\circ u)=\theta(G-Q')+1=\alpha(G)=\alpha(G\circ u)$。
定理十一: 在最小的(所有诱导子图都是 \gamma- 完美图)非 \gamma- 完美图中,任意一个独立集不可能和每个最大团相交。
证明:假如存在一个独立集 S 和每个最大团相交,那么由 G-S 的完美性得到 \chi(G-S)=\omega(G-S)=\omega(G)-1,此时给 S 中的元素染上同一种颜色,得到 \omega(G)=\omega(G-S)+1=\chi(G-S)+1=\chi(G)。矛盾。
定理十二(PGT):图 G 是完美的当且仅当图 \overline G 是完美的。
证明:显然这个定理和 \alpha- 完美与 \gamma- 完美等价是一样的。考虑一个最小的 \alpha- 完美但不是 \gamma- 完美的图。根据定理十一,可以假设它的每个最大独立集和一个最大团 Q(S) 不相交。
对 G 构造一个多重顶点复制。定义 S=\{S_i\} 为 G 的所有独立集,\{Q(S_i)
\} 为与 \{S_i\} 中每个最大独立集不相交的一个团组成得到的集合。对于每个节点 x_i,给它一个权值 h_i。h_i 等于 x_i 在 \{Q(S_i)\} 出现的频率。由定理十,H=G\circ h 是 \alpha- 完美的。现在我们试图找到一个矛盾。
将 \{Q(S_i)\} 和 V 之间的关系表示成一个矩阵 A。a_{i,j}=1 当且仅当 x_j\in Q(S_i)。这样,A 中 1 的个数等于 n(H),并且每行有 \omega(G) 个1。显然定点复制不会产生更大的团,故 n(H)=\omega(G)|S|=\omega(H)|S|。所以 \theta(G)\ge n(H)/\omega(H)=|S|。
下面我们试图通过证明 \alpha(H)<|S| 来得到矛盾。显然 H 的每个最大独立集都包含了 G 的每个最大独立集中的节点的所有复制。所以 \alpha(H)=\max\limits_{T\in S}\sum\limits_{i:x_i\in T}h_i。后面的和式计算了 A 中在 T 内的各个节点与 \{Q(S_i)\} 相交的个数,也就是每个节点代表的列上 1 的个数。按行来计数得到 \alpha(H)=\max
\limits_{T\in S}\sum\limits_{i:S_i\in S} |T\cap Q(S_i)|。由于 T 是独立集,所以对于每个 i 来说 T 中最多有 1 个顶点在 Q(S_i) 中。而 T 又不与 Q(T) 相交,故 |T\cap Q(S_i)|\le 1 且 |T\cap Q(T)|=0。由此得到 \alpha(H)< |S|。命题得证。