【日报】从背包问题来谈空间优化

## 前言 之前[洛谷日报](https://www.luogu.com.cn/blog/RPdreamer/bei-bao-wen-ti)也写过一篇背包来着，但这篇主要是讲背包问题上存在的空间优化，不过尽量将点比较基础的东西。 本人尚菜，图丑，轻喷。图片已经尽量做得色盲患者友好了。 ## 正文 ### $\bm {01}$ 背包的空间优化 例 $1$： > 有 $n$ 个物品，第 $i$ 个物品有体积 $v_i$，价值 $w_i$。现在有一个总体积为 $v$ 的背包，询问在恰好把它装满的前提下，用它最多能装下多少价值的物品。 > $1\le n\le 3\times 10^3$，$1\le v\le 2\times 10^4$，$1\le v_i\le v$，$1\le w_i\le 10^4$。 $n$ 个物品比较多，但我们可以从第 $n$ 个物品选还是不选开始入手。 - 如果选择了第 $n$ 个物品，那么问题转化为计算前 $n-1$ 个物品填充一个大小为 $v-v_n$ 的背包，所能获得的最大价值。这个价值加上 $w_n$ 就是在**钦定要选择**第 $n$ 个物品的情况下，所能获得的最大价值。 - 如果不选择第 $n$ 个物品，那就和第 $n$ 个物品没啥关系了，问题转化为计算前 $n-1$ 个物品填充一个大小为 $v$ 的背包，所能获得的最大价值。这个价值就是在**钦定不选择**第 $n$ 个物品的情况下，所能获得的最大价值。 也就是说，对于 $n$ 个物品的问题，只要考虑第 $n$ 个物品选不选，就可以转化为 $n-1$ 个物品的问题。同样地，$n-1$ 个物品的问题可以转化为 $n-2$ 个物品的问题，以此类推，可以一直转化为 $0$ 个物品的问题。 考虑记 $f_{i,j}$ 表示，在仅仅考虑前 $i$ 个物品的情况下，**装满**一个体积为 $j$ 的背包，所能获得的最大价值。同样是考虑第 $i$ 个物品选不选，那么就有： $$f_{i,j}=\max\{f_{i-1,j-v_i}+w_i,f_{i-1,j}\}$$ 举一个例子：$n=6$，$v=8$，$v=\{1,1,4,5,1,4\}$，$w=\{1,9,1,9,8,1\}$，最终得到的 $f$ 数组如下图所示：  观察 $\text{dp}$ 数组间的递推关系。  可以发现，我们可以根据上一行的 $\text{dp}$ 数组推断出下一行。因此可以从这个角度开始优化空间。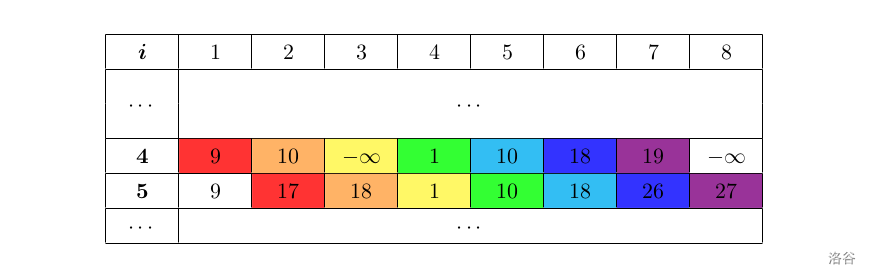 #### 思路 $\bm 1$：空间复用  我们希望用尽可能少的内存存储每一行的元素。最好希望只使用 $v$ 大小的数组，上一轮枚举存储的是第 $i-1$ 行的元素，在经过一轮枚举后就变成了第 $i$ 行的元素。 观察第 $5$ 行更新时使用第 $4$ 行元素的顺序。可以发现，当前处理的第 $5$ 行第 $j$ 列会使用第 $4$ 行第 $j-v_i$ 列的元素。如果从左往右更新第 $5$ 行，那么不可避免导致第 $4$ 行元素已经被覆盖，而第 $5$ 行还没成功更新。比如，当处理第 $5$ 行第 $3$ 列元素时，我们需要用到第 $4$ 行第 $2$ 列元素。如果从左往右枚举，那么在更新第 $5$ 行第 $2$ 列元素时已经覆盖了原来存储第 $4$ 行第 $2$ 列元素的内存。但是只要**从右往左枚举**，就不会发生这样情况。事实上，枚举的顺序与 $v_i$ 的正负有关（如果 $v_i$ 不全为正数的话）。当 $v_i>0$，应当从右往左枚举；当 $v_i<0$，应当从左往右枚举；$v_i=0$ 时两者均可。  #### 思路 $\bm 2$：开两个数组 由于计算第 $i$ 行时，只需要保留 $f$ 的第 $i-1$ 行，那么我们另开一个数组 $g$，用来存储第 $i-1$ 行的状态，$f$ 存储第 $i$ 行的状态，每次 $j$ 利用 $g$ 更新 $f$ 数组，循环一轮后 $f$ 数组完成更新，那就将 $f$ 复制到 $g$ 中即可。 这种做法的优点就是不用考虑应当从左枚举还是从右枚举。并且处理类似 $v_i$ 可正可负的情况比较简单。  不过这种做法每次滚动的时候要交换两个数组，常数较大。事实上只要交换两个数组的名字就可以做到滚动数组了，并且省去了交换两个数组带来的时间开销。  ### 完全背包的空间优化 例 $2$： > 有 $n$ 种物品，第 $i$ 种物品有无穷个，每个物品体积 $v_i$，价值 $w_i$。现在有一个总体积为 $v$ 的背包，询问在恰好把它装满的前提下，用它最多能装下多少价值的物品。 > $1\le n\le 3\times 10^3$，$1\le v\le 2\times 10^4$，$1\le v_i\le v$，$1\le w_i\le 10^4$。 考虑记 $f_{i,j}$ 表示，在仅仅考虑前 $i$ 个物品的情况下，**装满**一个体积为 $j$ 的背包，所能获得的最大价值。同样是考虑第 $i$ 个物品选不选，那么就有： $$f_{i,j}=\max\{f_{i,j-v_i}+w_i,f_{i-1,j}\}$$ 然后发现只要从左往右枚举就可以压缩到 $\mathcal O(m)$ 的空间复杂度了。不再赘述。  ### 多重背包的空间优化 例 $3$：[$\text{P1776}$ 宝物筛选](https://www.luogu.com.cn/problem/P1776) > 有 $n$ 种物品，第 $i$ 种物品有 $c_i$ 个，每个物品体积 $v_i$，价值 $w_i$。现在有一个总体积为 $v$ 的背包，询问用它最多能装下多少价值的物品。 > $1\le n\le 100$，$1\le \sum c_i\le 10^5$，$1\le v\le 4\times 10^4$。 #### 二进制拆分 二进制拆分优化的思路是，将每一种物品的 $c_i$ 个物品，划分为若干堆，每一堆物品再看成一个物品（有点绕口），这「一个」物品体积就是这堆物品的体积和，价值就是这对物品的价值和。这若干堆物品的特点是，选择其中的一些堆，它们可以组成 $0\sim c_i$ 当中任何一个物品。 例如，假定 $c_i=13$，而 $13=7+3+2+1$，那么这一种物品可以看成 $4$ 个物品，这四个物品的价值分别为 $7\cdot w_i,3\cdot w_i,2\cdot w_i,w_i$，体积分别为 $7\cdot v_i,3\cdot v_i,2\cdot v_i,v_i$。又因为： $$\begin{aligned} 13&=7+3+2+1 \cr 12&=7+3+2 \cr 11&=7+3+1 \cr \cdots \cr 2&=2\cr 1&=1 \end{aligned}$$ 因此用这 $4$ 个物品，就可以达到原先 $1$ 种物品、共 $13$ 个的效果。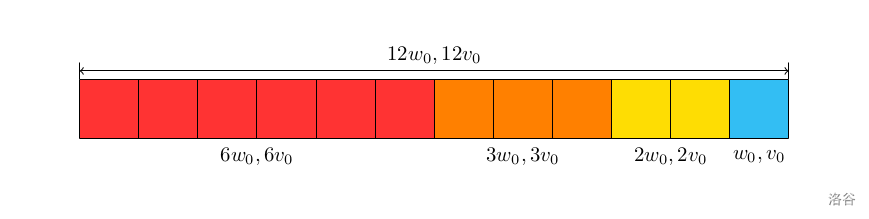  这个是 $c_i=12$ 拆成四个物品的例子。 二进制拆分的方法是简单的：假设现在要将 $c$ 个同种物品拆分下来，那么取出其中 $\left\lceil \frac{c}{2}\right\rceil$ 个物品作为一个物品，剩下来的 $c-\left\lceil \frac{c}{2}\right\rceil$ 进行递归拆分。子问题解决后，我们可以组合出 $0\sim \left(c-\left\lceil \frac{c}{2}\right\rceil\right)$ 中的任意一个数量；对于每个数量，再加上 $\left\lceil \frac{c}{2}\right\rceil$ 个物品作为的一个物品，又可以组合出 $\left\lceil \frac{c}{2}\right\rceil\sim c$ 当中任意一个数量。因此分出来的所有堆可以组合出 $0\sim c$ 中任意一个数量。 不过有些多重背包的二进制拆分做法，是真的把每个物品拆成 $\lceil\log v_i\rceil$ 个物品，然后跑一次 $01$ 背包。但这样子空间复杂度达到了 $\mathcal O(n\log c+v)$，能不能再优化一点呢？答案是显然的。我们没有必要先拆完了再跑 $01$ 背包，可以边跑边拆。具体而言，枚举当前处理到的物品种类 $i$，分出 $\left\lceil \frac{c_i}{2}\right\rceil$ 个物品跑一论，再将 $\left\lceil \frac{1}{2}\left(c-\left\lceil \frac{c_i}{2}\right\rceil\right)\right\rceil$ 个物品分出来跑一轮，以此类推，就用不着 $\mathcal O(n\log c)$ 的空间来存储所有拆出来的物品啦！ ~~虽然通常瓶颈不在空间，而在运行速度~~。同样给出伪代码：  #### 单调队列 既然要讲多重背包，那么单调队列顺带提一嘴。~~水字数~~。 假设我们要计算 $f_{i,j}$，那么显然 $f_{i,j}$ 的值只跟 $f_{i-1,j},f_{i-1,j-v_i},f_{i-1,j-2\cdot v_i},\cdots f_{i-1,j-c_iv_i}$ 有关。换言之，我们只考虑模 $v_i$ 与 $j$ 同余的那些下标。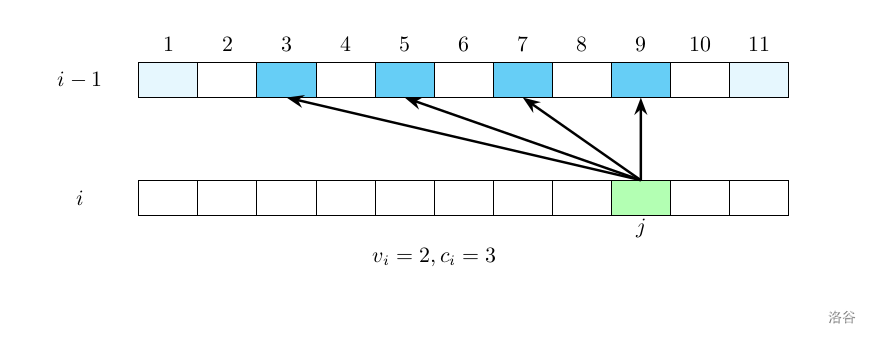  那么我们对每个同余系（即每次把模 $v_i$ 余数相同的那些 $j$ 放在一起考虑）分别处理。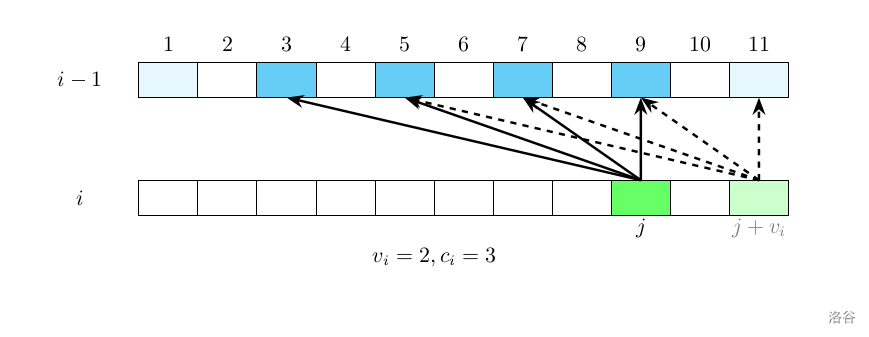考虑到： $$f_{i,j}=\max_{0\le k\le c_i}\{f_{i-1,j-kv_i}+w_ik\}$$ 设 $g_{j}=f_{i-1,j}-w_i\cdot\left\lfloor \dfrac{j}{v_i}\right\rfloor$，于是有： $$f_{i,j}=\max_{0\le k\le c_i}\{g_{j-kv_i}\}+w_i\cdot\left\lfloor \dfrac{j}{v_i}\right\rfloor$$  例如上图，所有蓝色（包括淡蓝色）的位置都是模 $2$ 同余的同余系，对于位置 $j$ 考虑的就是那四个深色的蓝色位置；下一个处理的是与 $j$ 同余的 $j+2$ 位置（图上标为浅绿色），它要考虑另外的四个蓝色位置（图中使用虚线箭头指向的）。 那么 $\max_{0\le k\le c_i}\{g_{j-kv_i}\}$ 这部分是可以使用单调队列优化的。这本质上是个滑动窗口问题。 有一种做法是，开 $v$ 个单调队列，一次性处理所有单调栈的问题。这样的缺点就是单调队列占用的空间较大（当然，如果你使用 $\text{STL}$ 里面的 $\text{queue}$，那么占用空间总和是 $\mathcal O(v)$ 的。但是这里讨论静态数组）。那么可以挨个处理每个同余系，这样只用开一个单调队列。  ### 树形背包的空间优化 大 的 药 来 了。 例 $4$：[$\text{P2014}$ [CTSC1997] 选课](https://www.luogu.com.cn/problem/P2014) > 有 $n$ 个物品，第 $i$ 个物品体积 $v_i$，价值 $w_i$，在选择第 $i$ 个物品前，需要选择第 $f_i$ 个物品。特别地，若 $f_i=0$ 则表示该物品没有前置物品需要选择。现在有一个总体积为 $v$ 的背包，询问在恰好把它装满的前提下，用它最多能装下多少价值的物品。 > $1\le n\le 300$，$1\le v\le 300$，$1\le v_i\le v$，$1\le w_i\le 20$。 首先假定有个物品 $0$，它价值为 $0$、体积为 $0$，所有 $f_i=0$ 的物品的前置物品就是这个物品 $0$。那么这所有物品的依赖关系就组成了一棵树，而非一个森林，便于我们求解。当然，因为物品 $0$ 的存在，$v$ 需要加上 $1$ 来处理这个多选择的物品 $0$。 现在假设 $f_{i,j}$ 表示在子树 $i$ 中，选择了恰好 $j$ 的体积，可以获得的最大价值。 现在假定我们已经计算好了一个节点 $u$ 所有子树的 $f$。那么我们考虑枚举 $u$ 的子节点，然后合并到 $f_u$ 上来。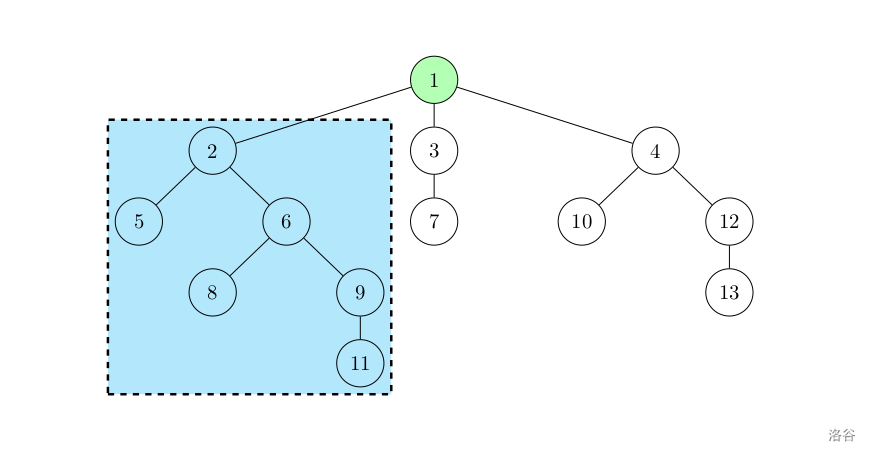如下图这个例子：  我们枚举整个子树 $1$ 所使用的空间 $i$，再枚举整个子树 $2$ 所使用的空间 $j$，然后进行更新： $$f_{1,i}\gets \max \{f_{1,i},f_{1,i-j}+f_{2,j}\}$$ 这样相当于把子树 $2$ 合并到了当前以 $1$ 为根的连通块上。不过应当注意的是，我们应该从大到小枚举这个 $i$，不然就相当于对每个子树做了一次完全背包。但实际上我们对子树做的是 $01$ 背包。合并其他子树同理。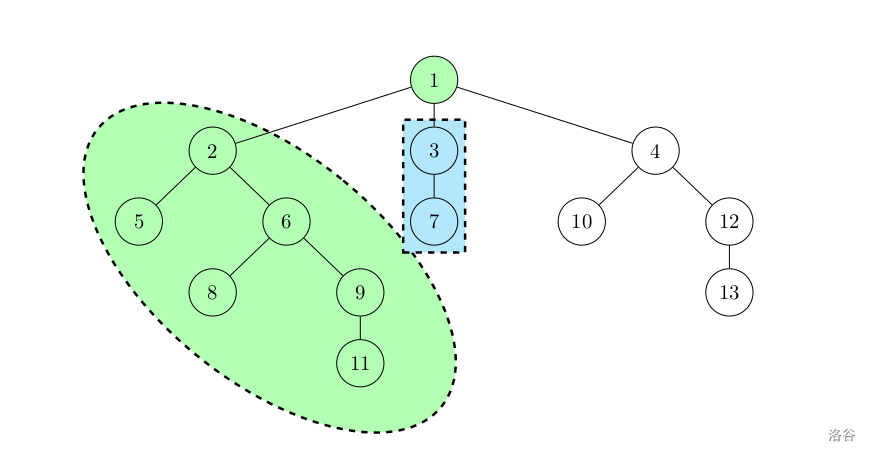  接着再把子树 $3$ 合并到以 $1$ 为根的连通块（所有绿色节点组成的区域）上。 $$f_{1,i}\gets \max \{f_{1,i},f_{1,i-j}+f_{3,j}\}$$ 上。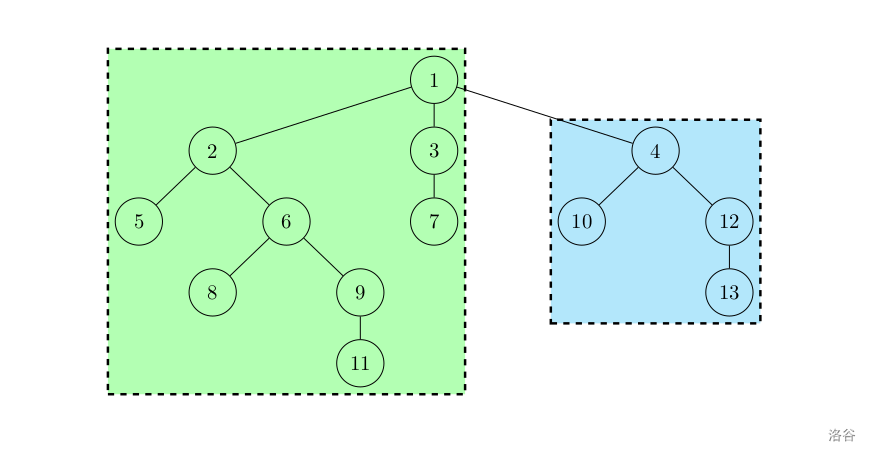  最后再把子树 $4$ 合并到以 $1$ 为根的连通块（所有绿色节点组成的区域） $$f_{1,i}\gets \max \{f_{1,i},f_{1,i-j}+f_{4,j}\}$$ 那么这个以 $1$ 为根的连通块，就已经完成了合并，变成了以 $1$ 为根的子树。往上回溯就能处理完整棵树。 然后就能发现，这个做法的空间复杂度为 $\mathcal O(nm)$。能不能再进行优化呢？ 考虑**重链剖分**。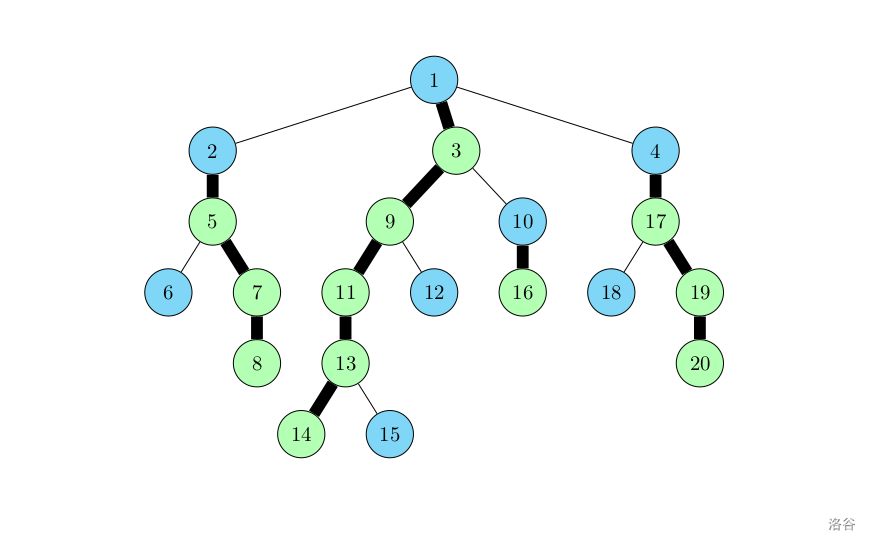  对于每个节点 $u$，取它最大的子树对应的根节点作为重儿子。图中蓝色节点是轻儿子/根节点，绿色节点为重儿子。以蓝色节点作为一条树链的起点，可以将整棵树剖分为若干条树链（图中黑色加粗部分）。 **引理**：一个大小为 $n$ 的树，按照子树大小进行重链剖分后，从根到达任意一个叶节点经过的重链数目（也可以理解成经过的蓝色节点的数目）不超过 $\lfloor \log _2n\rfloor+1$。 **证明**：使用归纳法。 - 对于大小为 $1$ 的树，显然根节点到达叶节点经过的重链数目为 $1$。 - 设结论对于 $n\le k$ 成立。那么对于一个节点个数为 $k+1$ 的子树 $u$，它的一个节点 $v$ 可以成为 $u$ 的一个重儿子，当且仅当子树 $v$ 的大小最大。那么如果一个节点 $v'$ 不能成为 $u$ 的重儿子，就说明子树 $v'$ 的大小不超过子树 $u$ 大小的一半，不然它必然是 $u$ 的重儿子。 - 如果 $u$ 经过 $v$ 到达叶节点，那么经过的重链条数的最大值就是从 $v$ 到达叶节点经过的重链条数的最大值，不超过 $\lfloor \log _2k\rfloor+1\le \lfloor \log _2(k+1)\rfloor+1$。 - 如果 $u$ 经过 $v'$ 到达叶节点，那么由于子树 $v'$ 的大小不超过 $\frac{(k+1)-1}{2}=\frac{k}{2}<k$，由归纳法，于是 $u$ 经过 $v'$ 到达根节点经过的重链个数不超过 $1+\left(\lfloor\log \frac{k}{2}\rfloor+1\right)=\lfloor\log k\rfloor+1\le \lfloor\log (k+1)\rfloor+1$。 证毕。 --- 回到本题上来。我们希望用尽量少的空间实现树形背包。直接 $\text{dfs}$ 的瓶颈在于，在回溯之前我们无法释放根节点到当前节点的这条链上，所对应的节点的 $\text{dp}$ 数组占用的空间。解决方法其实很简单：对于每条树链，我们只在它的链的顶端使用 $\text{dp}$ 数组。当深搜到这条树链上的点时，这个点要借用链顶节点的内存。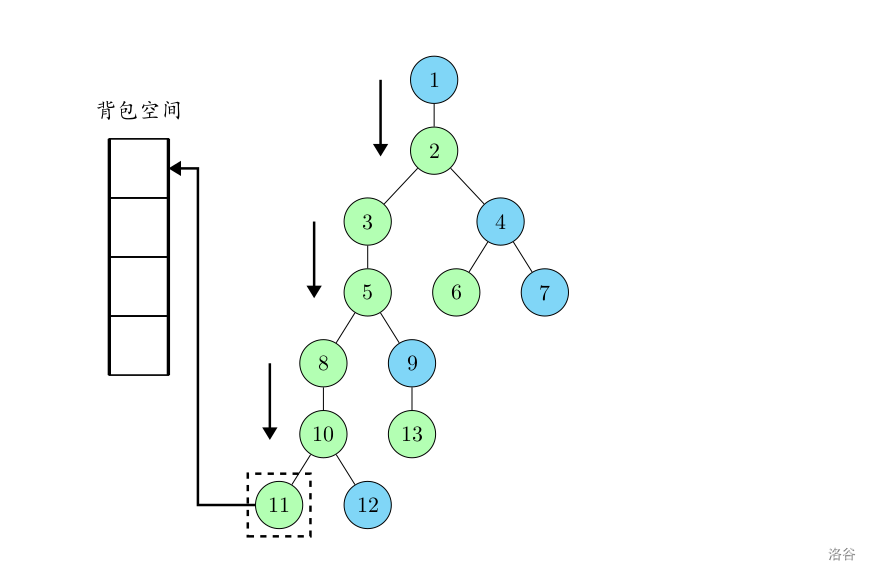 举个例子：  第一步，从根节点 $1$ 开始，沿着重儿子向下深度优先搜索，一直搜到叶子节点开始回溯。此时 $11$ 占用的数组位置就是第一位。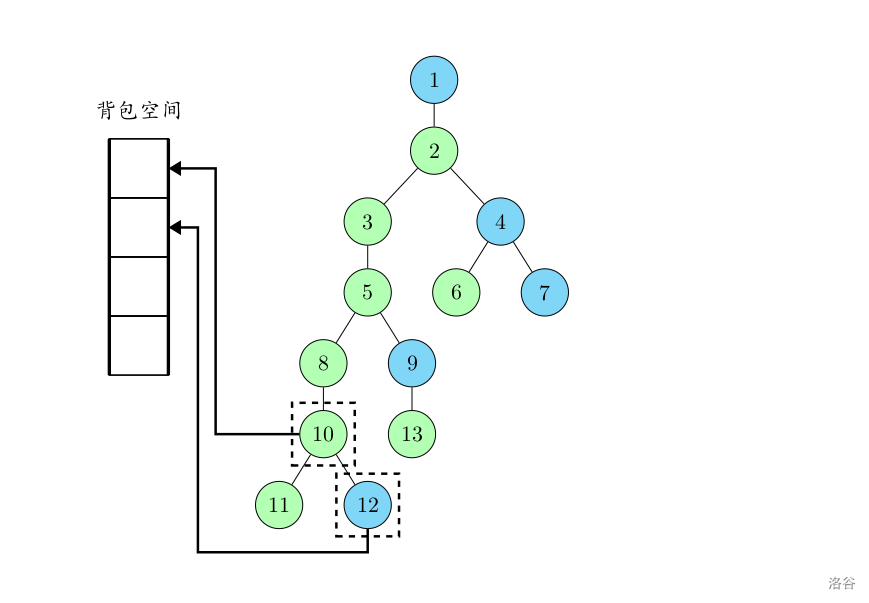  回溯到 $10$ 的时候，向下处理轻儿子 $12$。此时 $12$ 因为是新的树链的顶端，于是给他分配一个新的数组位置。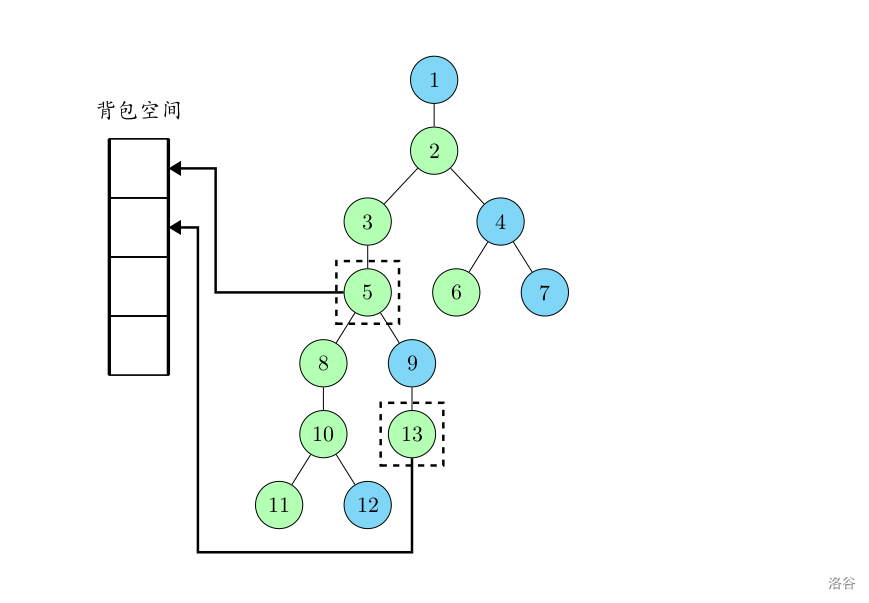  继续向上回溯，处理到了节点 $5$。此时向下处理它的轻儿子 $9$。从 $9$ 开始沿着重儿子链处理，使用的空间是数组的第二位。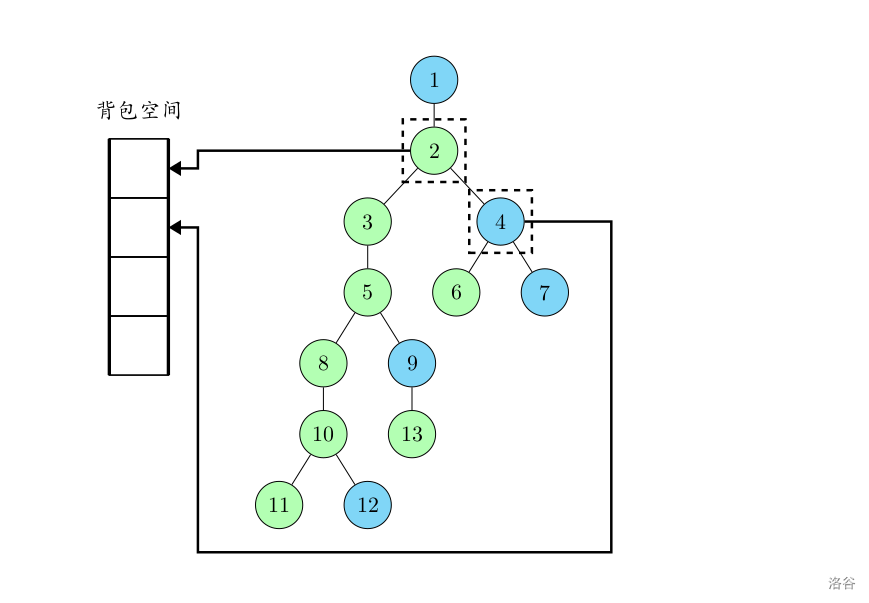  持续回溯，到了节点 $2$。处理它的轻儿子，节点 $4$ 向下搜索，处理完节点 $6$ 回溯到节点 $4$，接着处理 $4$ 的轻儿子节点 $7$。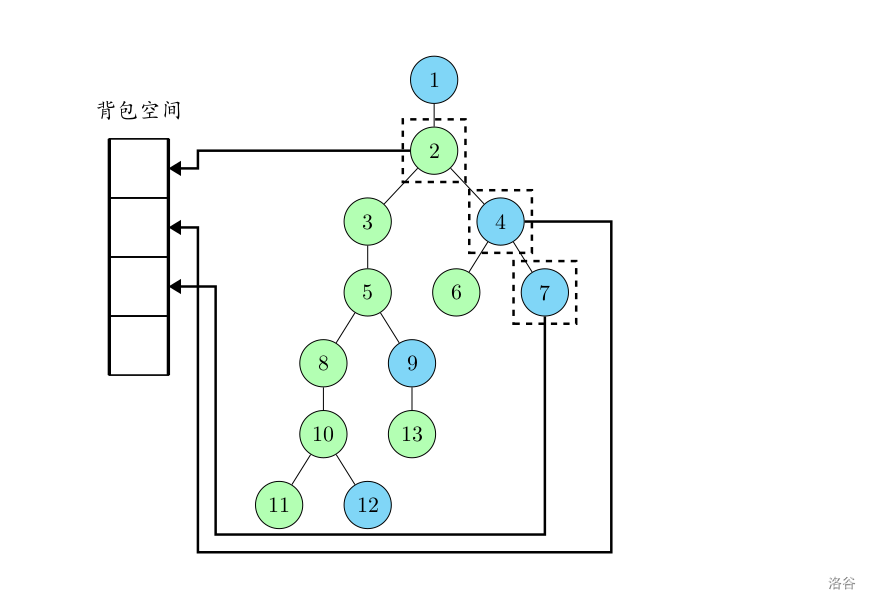  因为节点 $7$ 是轻儿子，所以需要给它开一个新的数组位置。  最后回溯到根节点，此时根节点所使用的数组的第一位就是 $f_{1,0\sim v}$。 根据刚刚的结论，从根节点到任意叶子节点经过的轻儿子个数不超过 $\lfloor\log_2 n\rfloor+1$，因此总空间复杂度为 $\mathcal O(v\log_2 n)$。  ### 可撤回背包（离线）的空间优化 一 转 攻 势。 例 $5$：[$\text{P5391}$ [Cnoi2019]青染之心](https://www.luogu.com.cn/problem/P5391) > 有一个大小为 $v$ 的背包，现在你有 $q$ 个操作，分为两种： > - `add x y` : 表示加入一种体积为 $x$, 价值为 $y$ 的物品到序列末尾； > - `erase` : 表示删除序列末尾的物品。 > 每个操作结束以后，你需要求出： > - 假设序列中的每种物品都有无穷多个，这个背包背包可以装下的物品最大价值和。 > $1\le q,v,x,y\le 2×10^4$。 因为需要支持撤回操作，所以滚动数组行不通了。$\mathcal O(qv)$ 的空间复杂度会空间爆炸。 那么先考虑往序列后面增加物品、删除物品对当前物品序列的改变。物品序列可以看作一个线性的结构，增加物品只需要在这个结构后面加一个节点即可。但是删除物品，**不一定非得将最后一个位置擦除**。使用变量 $p$ 维护物品序列最后一个物品的位置，然后就可以软删除。那么，在增加物品的时候也可以不把原来被「废弃」的位置覆盖掉，而是可以开出一个新的分支。换言之，此时这个物品序列成为了一棵**物品树**。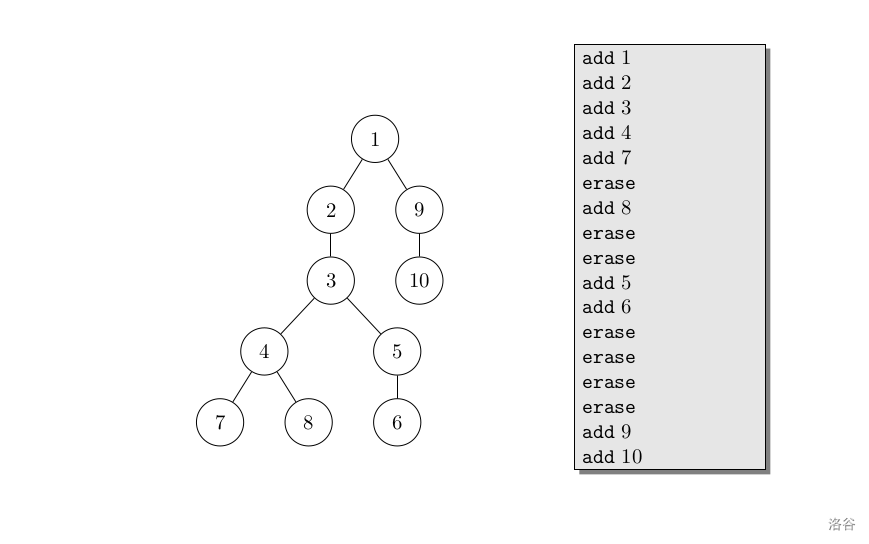  （为了方便起见，图中的 $\verb!add!$ 的定义和题面并不一样。$\verb!add!$ 后面的数字是对应物品的编号）。 那么可以将所有操作离线下来把这棵物品树建起来。根据刚刚的经验，对它进行树链剖分。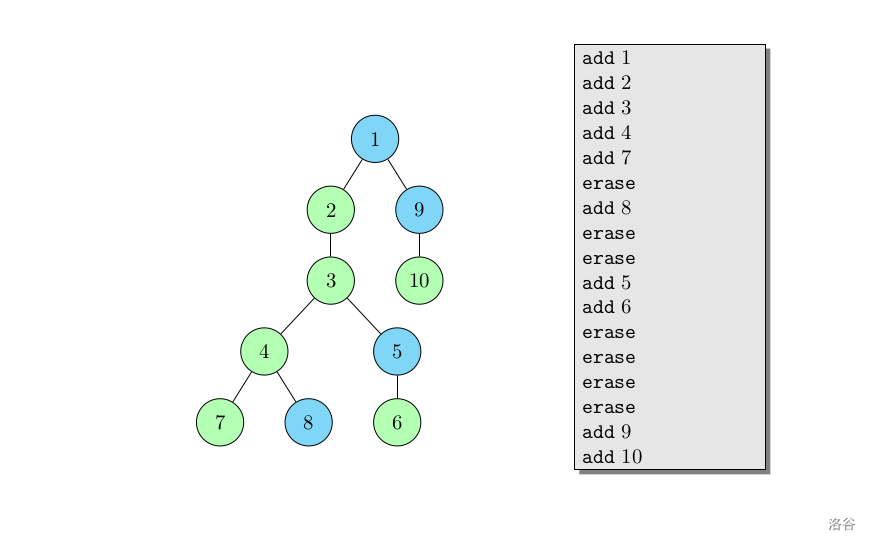  不过这次树形 $dp$ 的状态转移方程和上题有所不同。我们记 $f_{i,j}$ 表示，操作序列中的物品为 $1$ 到 $i$ 的路径上所有的物品节点组成的物品，使用了 $j$ 的空间，所能够得到的最大物品价值。容易得到状态转移方程： $$f_{i,j}=\max\{f_{\operatorname{fa}(i),j},f_{i,j-v_i}+w_i\}$$ 注意：这次每个结点的 $dp$ 数组仅由它的父亲转移而来，而上一例中，则是由它的所有儿子转移而来。但是我们仍然对于每个树链，只在它的链顶（轻儿子）开 $\mathcal O(v)$ 的空间。不过要稍微修改一下搜索的方式： - 首先把当前节点的**轻儿子**进行处理。处理轻儿子的时候需要额外开辟内存。 - 然后再处理**重儿子**。处理重儿子的时候不需要额外使用内存，这样就大大减小了空间开支。 为什么要最后处理重儿子呢？因为重儿子不会开新的内存，那么在旧的内存上更新后，原来的信息就没有了。此时就无法处理轻儿子。但是当轻儿子处理完后，旧的内存就没用了，可以留给重儿子使用。 由于该例做法与上一例几乎一致，因此不给出图片分解了。（上一例画图画的累死我了）。另外，因为有可能所有物品都 $\verb!erase!$ 完了，这个时候就可能形成森林。为了避免这个情况，所以物品树上应该弄个根节点 $0$，对应的物品的体积为 $1$（防止完全背包炸了），价值为 $0$，对应啥物品都没有的状态。 同样是上一例的结论，从根到达每个叶子节点，经过的轻儿子个数不超过 $\lfloor \log n\rfloor+1$。因此总的空间复杂度为 $\mathcal O(v\log n)$。  ### 可撤回背包（在线）的空间优化 图 穷 匕 见。 例 $6$： > 初始时原材料会有一个初始权值。然后它会经过若干个机器的加工，花费若干点**加工指数**，得到最终产品。 > 河童的机器有两种： > - 0 型：每次加工花费 $v_i$ 的加工指数，让材料的附加值增加 $w_i$。材料经过时**最多只能加工一次**。 > - 1 型：每次加工花费 $v_i$ 的加工指数，让材料的附加值增加 $w_i$。材料经过时**加工次数无限制**。 > 现在河童会利用一个机械臂来设计这套工艺流程。初始时，流水线上没有一台机器，机械臂放在位置 $0$。机器的位置编号是从 $1$ 开始的。现在河童会告诉你加工指数的最大值 $v$，然后她会下达 $q$ 个命令。不妨设每个指令执行前，机械臂的位置在 $p$。 > 每个指令的格式为 $\colorbox{#f0f0f0}\verb!opt ti vi wi xi yi!$，其中 $opt$ 表示操作的种类。共有如下几种： > 1. **右移**：将机械臂向右移动一格，即 $p\gets p+1$。 > 2. **左移**：将机械臂向左移动一格，即 $p\gets p-1$。 > 3. **插入机器**：在机械臂当前位置插入一个机器，它的类型为 $t_i$，每次消耗的加工指数为 $v_i$，材料的附加值会增加 $w_i$，插入的机器的位置为 $p+1$。机械臂位置不变，但是被插入的机器右侧的机器都会向右移动一格。 > 4. **删除机器**：在机械臂当前位置移除一个机器，移除的机器位置为 $p+1$。移除机器后机械臂位置不变，但是被移除的机器右侧的机器都会向左移动一格。 > 5. **修改机器**：在机械臂当前位置修改一个机器的参数。即修改的机器的位置为 $p+1$。 > 对于操作 1, 2, 4，请忽略参数 $\colorbox{#f0f0f0}\verb!ti vi wi!$。 > 每次操作完，河童会询问你，如果一个初始权值为 $x_i$ 的物品从左侧起第一个机器进去，直到从右边机器出来，依次加工，消耗最多 $y_i$ 点加工点数（ $y_i\le v$ ），这个物品可以获得的最大权值。特别地，如果此时没有一台机器，此物品权值不变。 > 假设某一时刻共有 $u$ 台机器，那么数据保证在此时刻机械臂的位置必然在 $[0,u]$ 内。 一眼扫过该题，你会发现它是个背包板子。先不考虑其他问题，让我们想想朴素的背包做法怎么做。 如果你接触过对顶堆一类的简单科技，你会发现这题相当于将两个背包问题拼接在了一起。首先实现一个简单的数据结构（？），不妨称为背包栈。它应该支持在顶部插入一种物品，弹出顶部的那种物品，以及快速查询，一个空间为 $v_0$ 的背包能装下的最大价值是多少。简要的实现办法如下： - 用 $dp_{i,j}$ 表示前 $i$ 个物品，使用不超过 $j$ 的空间可以获得的最大价值。 - 现在加入了一个物品 $(v_i,w_i,t_i)$ ,表示它的体积为 $v_i$，价值为 $w_i$，类型为 $t_i$ （只有一个，还是有无穷个）。那么转移方程如下： $$dp_{u,i}=\max\{dp_{u-1,i},dp_{u,i},dp_{u,i-v_i}+w_i\}$$ 它的枚举顺序与 $t_i$ 相关。其中，$u$ 表示当前这个物品序列中有多少个物品。 - 删除一个物品就更简单了，你只需要 $u\gets u-1$ 就行了。 回到正题，你现在实现了这样的数据结构，按照对顶堆的样子放在一起。显然需要两个背包栈，不妨称为 $\mathit{Bag}_1,\mathit{Bag}_2$。考虑如何完成题目中要求的五种操作。两个结构的顶端相对。 - 机械臂向右移动。只要弹出 $Bag_2$ 顶端的物品，然后插入到 $Bag_1$ 顶端即可。 - 机械臂向左移动。只要弹出 $Bag_1$ 顶端的物品，然后插入到 $Bag_2$ 顶端即可。 - 插入一个物品。这一部分也很简单，你直接向 $Bag_2$ 顶部插入一个物品即可。 - 删除一个物品。与插入物品类似，改为移除 $Bag_2$ 顶部的物品。 - 修改一个物品。比较简单的做法就是直接弹出 $Bag_2$ 顶部，然后再插入一个物品。 容易发现，这样空间复杂度为 $\mathcal O(vq)$，在本题会 $\text{MLE}$。下面考虑如何优化这个背包栈。 --- 如果你接触过简单背包问题，那么你应该知道滚动数组优化。可惜的是，这题因为需要支持弹出操作，而滚动数组会丢失掉很多信息，所以朴素的滚动数组是会出锅的。但这不妨是一个很好的启发。 于是考虑分块。~~这思维跳跃也太生硬了吧~~。 由于操作 $1,2$ 的存在，于是每次操作的位置都是相邻的。考虑记录 $p\in[l,r]$ 时的所有 $dp$ 信息，那么当 $p$ 在这个范围内游走时就可以直接取出对应的 $dp$ 数组了。我们不能无限制开大 $r-l$ 的大小，于是不妨设 $s=r-l$，其中 $s$ 是常数。这部分空间复杂度是 $\mathcal O(vs)$ 的。下面考虑 $p$ 跃出这个范围应该如何处理。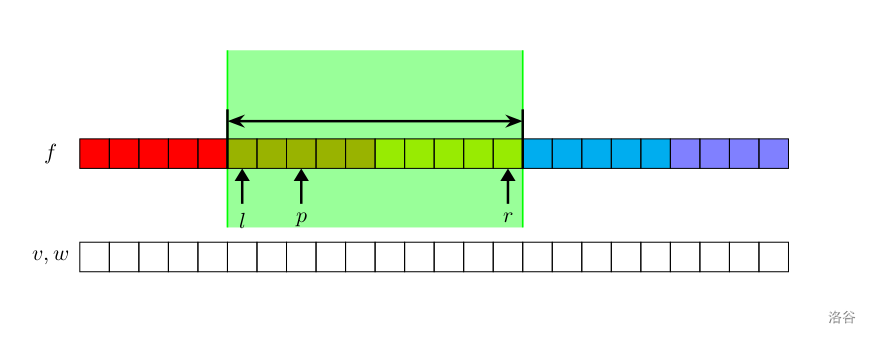  如图所示，我们将 $f$ 数组的第一维分成 $n/s$ 个块，每一块的长度为 $s$。$l,r$ 指针是我们维护的 $dp$ 数组的区域，$p$ 指针是当前河童机械臂 $u$ 所在的位置对应的 $dp$ 数组的第一维下标。图中绿色部分就是我们在 $dp$ 数组上的空间开销。 背包问题有个非常好的性质，当你知道了 $dp_{u,x}(x\in[0,v])$，以及它后面一些物品的属性（大小、价值），你就能快速生成 $dp_{u+1,x},dp_{u+2,x}\cdots$。不妨记录 $u\equiv 0\pmod{s'}$ 时的 $dp_{u,x}$ 作为关键点，其中 $s'$ 是常数。当 $u$ 跨出 $[l,r]$ 时就对它进行调整（比如，$u<l$ 时就 $l\gets l-s',r\gets r-s'$ ），然后花费 $\mathcal O(vs)$ 的时间重新生成这一部分的 $dp$ 数组。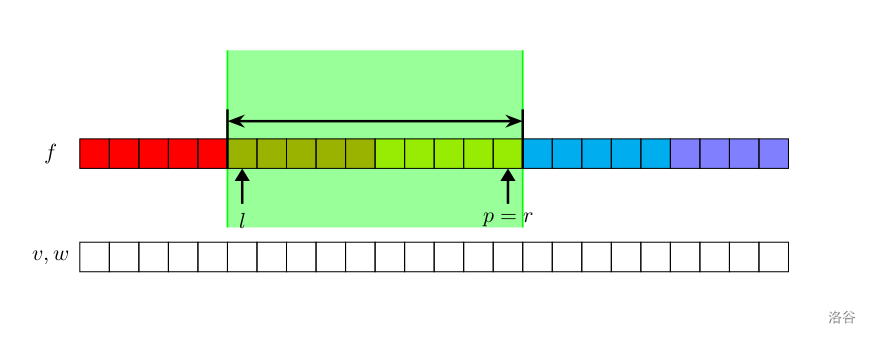  这张图是 $p$ 到达了已知信息边界的情况。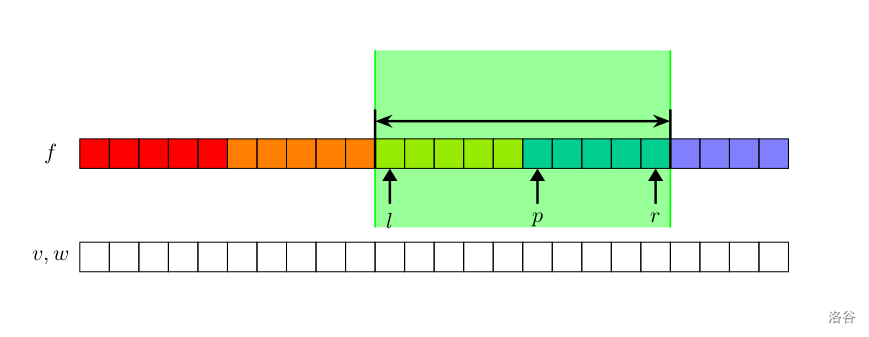  这张图中，$p$ 跳出了右边界。因此我们同步更新 $l$ 指针和 $r$ 指针，并且花费 $\mathcal O(vs)$ 的时间复杂度更新已经维护的 $dp$ 区域。 下面考虑确定常数 $s$ 具体的值，来达到最佳的空间优化的效果。 初始时，显然 $l=0,r=s$。我们希望每次更新 $l,r$，都使得 $u$ 在 $l,r$ 的中点，这样子到下一次更新需要更新 $u$ 的次数最少。于是令 $s'=\frac{1}{2}s$。每次更新 $l,r$，时间复杂度是 $\mathcal O(vs)$。最坏情况下要更新 $\frac{q}{s'}$ 次，于是时间复杂度是 $\mathcal O(vq)$，这是没有问题的。关键点的数目是 $\frac{q}{s'}$，每个关键点都要维护 $\mathcal O(v)$ 的空间，这部分空间是 $\mathcal O(v\cdot \frac{q}{s'})$。同时维护 $[l,r]$ 也要花费 $ \mathcal O(vs)$，所以总共花费的空间复杂度是 $\mathcal O(v\cdot(\frac{q}{s'}+s))$，取 $s=\sqrt{\frac{q}{2}}$ 可以得到最小的空间复杂度。 总时间复杂度 $\mathcal O(vq)$，空间复杂度 $\mathcal O(v\sqrt q)$，可以通过本题。   ## 习题 哪有神秘出题人卡背包的空间。所以没有课后习题。