0. 头文件与常数
#include <iostream>
#include <cmath>
#include <vector>
#include <complex>
using namespace std;
const double EPS = 1e-6, Pi = 3.141592653589793;
本篇文章涉及到大量人类智慧
有错误或疏漏请及时在评论区指出或私信
1. 一次方程
形如 ax+b=0 (a\neq0) 的方程叫做一次方程,最简单的方程,小学五年级知识。
解法
- 首先移项,变为 ax=-b;
- 两边同时除以 a,解得一次方程求根公式 \boxed{x=-\dfrac ba}。
例:解方程 2x+6=0。
解:代入求根公式得 x=-\dfrac ba=-\dfrac62=3。
代码
double solve1(double a, double b)
{
return -b / a;
}
真没啥可说的,注意 a\neq0,考试坑死人。
2. 二次方程
形如 ax^2+bx+c=0 (a\neq0) 的方程叫做一元二次方程,初中二年级知识。
配方法
配方法,顾名思义,就是将一个式子或其中的某一部分通过恒等变形化为完全平方式或几个完全平方式的和。
对于二次方程的配方,我们需要用到完全平方公式:a^2+b^2+2ab=(a+b)^2。
解法
- 方程两边同时除以最高次项系数 a,移项后得 x^2+\dfrac bax=-\dfrac ca;
- 左边利用完全平方公式配方得 \left(x+\dfrac{b}{2a}\right)^2-\dfrac{b^2}{4a^2}=-\dfrac ca;
- 移项后得 \left(x+\dfrac{b}{2a}\right)^2=\dfrac{b^2-4ac}{4a^2};
- 两边同时开平方,得 x+\dfrac{b}{2a}=\pm\dfrac{\sqrt{b^2-4ac}}{2a};
- 移项后解得二次方程求根公式 \boxed{x=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}}。
求根公式中根号下的东西叫二次方程的判别式,\Delta=b^2-4ac。
- 若 \Delta>0,方程有两不等实根:x_1=\dfrac{-b+\sqrt \Delta}{2a},x_2=\dfrac{-b-\sqrt \Delta}{2a};
- 若 \Delta=0,方程有两相等实根:x_1=x_2=-\dfrac{b}{2a};
- 若 \Delta<0,方程无实根,有两复数根:x_1=\dfrac{-b+\text{i}\sqrt{-\Delta}}{2a},x_2=\dfrac{-b-\text{i}\sqrt{-\Delta}}{2a}。
当根为整数时,解二次方程也可使用十字相乘法。
例:解方程 x^2+3x+2=0。
解:十字相乘后分解因式得:(x+1)(x+2)=0,解得两根分别为 x_1=-1,x_2=-2,与求根公式求得的两根相同。
代码
pair<complex<double>, complex<double> > solve2(double a, double b, double c)
{
double delta = b * b - 4 * a * c;
if(delta > 0)
{
double x1 = (-b + sqrt(delta)) / (2 * a), x2 = (-b - sqrt(delta)) / (2 * a);
return {{x1, 0}, {x2, 0}};
}
if(delta == 0)
{
double x1 = -b / (2 * a), x2 = x1;
return {{x1, 0}, {x2, 0}};
}
if(delta < 0)
{
double x_re = -b / (2 * a), x1_im = sqrt(delta) / (2 * a), x2_im = -sqrt(delta) / (2 * a);
return {{x_re, x1_im}, {x_re, x2_im}};
}
}
事实上,在 OI 中,复数根用处不算很大,所以在保证 \Delta\ge 0 的情况下,程序可简化成:
pair<double, double>, solve2(double a, double b, double c)
{
double delta = b * b - 4 * a * c;
double x1 = (-b + sqrt(delta)) / (2 * a), x2 = (-b - sqrt(delta)) / (2 * a);
return {x1, x2};
}
图像性质
中学阶段(尤其是初中)最重要的函数就是二次函数,所以这里让我扯两句关于二次函数图像的性质。
二次函数图像是关于一条对称轴对称的;两根分布于对称轴的两侧,与对称轴距离相等,关于对称轴对称。
对于任意二次函数 f(x)=ax^2+bx+c (a\neq0),求导得 f'(x)=2ax+b。当 f'(x)=0 时,对称轴 x=-\dfrac{b}{2a},也是二次函数极值点的 x 坐标。
将 x=-\dfrac{b}{2a} 代入 f(x),得到 f(x) 的极值点 \boxed{\left(-\dfrac{b}{2a},-\dfrac{\Delta}{4a}\right)}。
若 a>0,则在极值点时函数取得最小值;
若 a<0,则在极值点时函数取得最大值。
韦达定理(根与系数的关系)
对于任意二次方程 ax^2+bx+c=0 (a\neq0),两根 x_1,x_2 有关系:
x_1+x_2=-\dfrac ba\\
x_1x_2=\dfrac ca
\end{matrix}\right.
证明可由求根公式直接推得,这里不详细说明。
逆定理:如果两数 \alpha,\beta 满足 \alpha+\beta=-\dfrac ba,\alpha\beta=\dfrac ca,则 \alpha,\beta 为方程 ax^2+bx+c=0 的两根。
通过逆定理,可以利用两数的和积关系构造一元二次方程,在数学竞赛中常用。
韦达定理的推广
设一元 n 次方程 a_nx^n+a_{n-1}x^{n-1}+\dots+a_1x+a_0=0 的根为 x_1,x_2,\dots,x_n,则有:
x_1+x_2+\dots+x_n=-\dfrac{a_{n-1}}{a_n}
x_1x_2\dots x_n=(-1)^n\dfrac{a_0}{a_n}
证明:
建议手推一遍,有助于加深理解
众所周知,一元五次及以上的方程没有通用的求根公式,所以不能直接通过求根公式来推出根系关系。
那么怎么办呢?
设一元 n 次方程 a_nx^n+a_{n-1}x^{n-1}+\dots+a_1x+a_0=0 的根为 x_1,x_2,\dots,x_n,那么这个 n 次方程也可以表达成另一种形式:a_n(x-x_1)(x-x_2)\dots(x-x_n)=0。
接下来对比原方程和变形后的方程的系数。如何找到 x^k 的系数呢?
我们可以在变形后的方程中的 n 个因式 (x-x_i) 中,任选 k 个 x 相乘得到 x^k;
然后在剩下的 n-k 个因式中选择 -x^i,就得到了 x^k 的系数(别忘了乘上最前面的 a_n!):
例如我们想要得到 $x^{n-1}$(此时 $k=n-1$),我们可以在 $n-1$ 个因式中选择 $x$ 相乘,并在剩下的 $1$ 个因式中选择 $-x^i$ 相乘,因此系数就是 $a_n\times-(x_1+x_2+\dots+x_n)=a_{n-1}$。
因此
$$x_1+x_2+\dots+x_n=-\dfrac{a_{n-1}}{a_n}$$
同理可得
$$x_1x_2+x_1x_3+\dots+x_2x_3+\dots+x_{n-1}x_n=\dfrac{a_{n-2}}{a_n}$$
$$\vdots$$
$$x_1x_2\dots x_n=(-1)^n\dfrac{a_0}{a_{n}}$$
将 $n=2$ 代入,发现与二次方程的韦达定理形式一样。
# 3. 三次方程
### 接下来两章的例题:[洛谷P1024](https://www.luogu.com.cn/problem/P1024)
形如 $ax^3+bx^2+cx+d=0$ $(a\neq0)$ 的方程叫做一元三次方程。
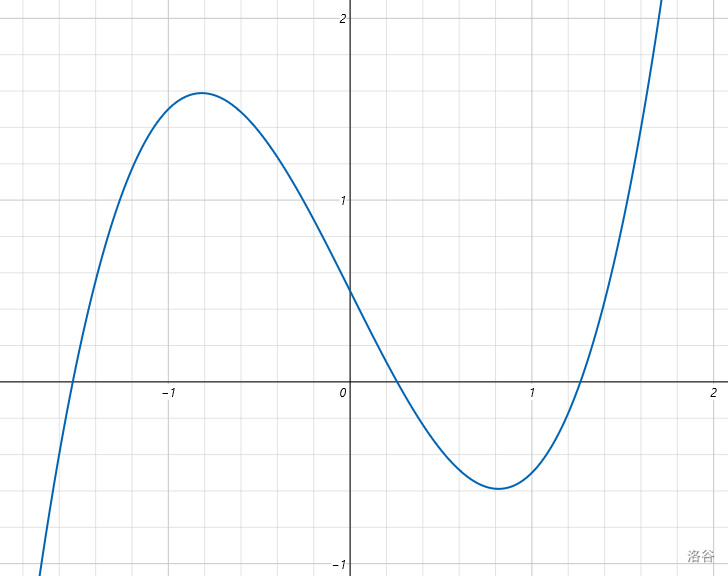
> 图:${\color{Blue}f(x)}=x^3-2x+0.5$,from Windows Calculator
解此类方程中学一般采用因式分解和试根法。
## 试根法
试根法,顾名思义,就是把整系数方程的根一个一个试出来。
令 $n$ 次**整系数**多项式为 $a_0+a_1x+a_2x^2+\dots+a_nx^n$,函数 $f(x)=a_nx^n+a_{n-1}x^{n-1}+\dots+a_1x+a_0$,其中 $a_0,a_1,\dots,a_n\in\mathbb{Z}$。
### 余数定理
**定理**:如果 $f(x_0) = 0$,那么 $(x-x_0)$ 是 $f(x)$ 的因式;反过来也成立。
显然成立,不证明。
### 有理根求法
**定理**:若方程存在有理根 $x_0$,则有理根 $x_0=\dfrac pq$($p,q$ 互质)的分子 $p$ 是常数项 $a_0$ 的因数,分母 $q$ 是最高次项系数 $a_n$ 的因数。
证明:
1. 因为 $f(x_0)=0
- 所以 a_n\left(\dfrac pq\right)^n+a_{n-1}\left(\dfrac pq\right)^{n-1}+\dots+a_1\left(\dfrac pq\right)+a_0=0
- 同乘 q^n 得 a_np^n+a_{n-1}p^{n-1}q+\dots+a^1pq^{n-1}+a_0q^n=0\quad(*)
- 因为 (*) 式右边为 0,能被 p 整除,所以左边也能被 p 整除。
- 显然左边前 n 项都能被 p 整除,所以最后一项 a_0q^n 也能被 p 整除。
- 但 p 与 q 互质,所以 p 整除 a_0,p 是 a_0 的因数。
- 同理,q 是 a_n 的因数。
试根方法
由上可得试根方法:
- 分别列出 a_0 的因数 p_1,p_2,\dots,p_{k_1} 和 a_n 的因数 q_1,q_2,\dots,q_{k_2}。
- 将所有的 p 分别除以所有的 q,就得到所有可能的 x_0。
- 把这些可能的 x_0 一个一个试,如果 f(x_0)=0,那么方程存在一个根 x_0。
例:解方程 x^3+8x^2+17x+6=0。
解:
- 列出 a_0=6 的因数 \pm1,\pm2,\pm3,\pm6;列出 a_n=1 的因数 \pm1。
- 将 a_0 的因数和 a_n 分别相除,得到可能的根 \pm1,\pm2,\pm3,\pm6。
- 记 f(x)=x^3+8x^2+17x+6。
- 试根,发现只有 f(-3)=0,得到方程的一个因式 (x+3),即方程的一个根 x_1=-3。
- 大除法,将 x^3+8x^2+17x+6 除以 x+3 ,得因式 x^2+5x+2。
- 解二次方程 x^2+5x+2=0,得方程的另外两根 x_2=\dfrac{-5+\sqrt{17}}{2},x_3=\dfrac{{-5}-\sqrt{17}}{2}。
中学阶段解高次方程的通用方法就是:因式分解 \rightarrow 试根 \rightarrow 因式分解 \rightarrow 试根 \rightarrow \dots \rightarrow 解低次方程。
简便判别法
一个一个根试太麻烦了!有没有什么简单的方法?
简便判别法:如果 q-p 不是 f(1) 的因数,那么 \dfrac pq 不是 f(x) 的根。
证明:
- 假设 \dfrac pq 是 f(x) 的根。
- 则由余数定理得 f(x)=(qx-p)Q(x),其中 Q(x) 是整系数多项式。
- 令 x=1,得 f(1)=(q-p)Q(1)。
- 因为 Q(x) 是整系数多项式,所以 Q(1)\in\mathbb{Z},所以 q-p 是 f(1) 的因数。
- 因此,q-p 不是 f(1) 的因数时,\dfrac pq 不是 f(x) 的根。(逆否命题)
注意:此判别法只能判定 \dfrac pq 不是根。在 q-p 是 f(1) 的因数时,并不能判定 \dfrac pq 是 f(x) 的根。
注:当最高次项系数为 1 时,有理根都是整数根。
注:如果 f(x) 的系数是有理数,即分母不全为 1,那么提取一个分数因数(分母是各个系数的公分母)后就可化为整系数多项式的情况。
代码
// 求整系数三次方程的一个根
// ax^3 + bx^2 + cx + d = 0 (a != 0)
double solve3(int a, int b, int c, int d)
{
vector<int> p, q;
for(int i = 1; i <= abs(d); i++)
if(abs(d) % i == 0)
{
p.push_back(i);
p.push_back(-i);
}
for(int i = 1; i <= abs(a); i++)
if(abs(a) % i == 0)
{
q.push_back(i);
q.push_back(-i);
}
for(int p_i : p)
for(int q_i : q)
{
long double x0 = 1.0 * p_i / q_i;
if(abs(a * x0 * x0 * x0 + b * x0 * x0 + c * x0 + d) < EPS)
return x0;
}
}
求根公式
注:以下内容中学阶段不讲(大概吧)
写了这么多,那有没有通用的求根公式呢?有的。先上公式:
对于 ax^3+bx^2+cx+d=0 (a\neq0),其通解为:
x_1=-\dfrac{b}{3a}+\sqrt[3]{\dfrac{bc}{6a^2}-\dfrac{b^3}{27a^3}-\dfrac{d}{2a}+\sqrt\Delta}+\sqrt[3]{\dfrac{bc}{6a^2}-\dfrac{b^3}{27a^3}-\dfrac{d}{2a}-\sqrt\Delta}
x_2=-\dfrac{b}{3a}+\omega\sqrt[3]{\dfrac{bc}{6a^2}-\dfrac{b^3}{27a^3}-\dfrac{d}{2a}+\sqrt\Delta}+\omega^2\sqrt[3]{\dfrac{bc}{6a^2}-\dfrac{b^3}{27a^3}-\dfrac{d}{2a}-\sqrt\Delta}
x_3=-\dfrac{b}{3a}+\omega^2\sqrt[3]{\dfrac{bc}{6a^2}-\dfrac{b^3}{27a^3}-\dfrac{d}{2a}+\sqrt\Delta}+\omega\sqrt[3]{\dfrac{bc}{6a^2}-\dfrac{b^3}{27a^3}-\dfrac{d}{2a}-\sqrt\Delta}
其中判别式 \Delta 为:
\Delta=\left(\dfrac{bc}{6a^2}-\dfrac{b^3}{27a^3}-\dfrac{d}{2a}\right)^2+\left(\dfrac{c}{3a}-\dfrac{b^2}{9a^2}\right)^3
三次单位根 \omega 为:
\omega=\dfrac{-1+\sqrt3\text i}{2}
一元三次方程必存在至少一个实数解,为 x_1。
发明历史
说了这么多数学,来扯两句历史。
论文链接 (这都能写篇论文我是真没想到)
三次方程求根公式最早在 16 世纪分别由两位意大利数学家独自发现:Nicolo Tartaglia(塔尔塔利亚)与 Scipione del Ferro(费罗)。那时的数学家喜欢在数学对决中互相比拼,他们喜欢出数学难题来挑战其他的数学家。所以,他们都没有公开发表这一求根公式。
当大家都知道了塔尔塔利亚有求根公式后,Gerolamo Cardano(卡尔达诺)开始追随塔尔塔利亚学习求根公式。塔尔塔利亚把求根公式隐藏在了一首 藏头诗 中,告诉了卡尔达诺,并要求他保密。
之后,卡尔达诺在费罗的笔记本中也发现了三次方程求根公式,所以他就将公式发表在自己的书《大法》里,后人就把这一公式称为卡尔达诺公式。
书中顺便还记载了由卡尔达诺的学生 Ferrari Lodovico(费拉里)所发现的四次方程的求解方法(好像不是求根公式,因为实在太长了)。
推导过程 - Part 1
建议手推一遍加深理解
可参考 Mathologer 的视频。
对于三次方程,自然先想到能不能用类似二次方程的配方法来解?
- 先约去最高次项
x^3+\dfrac bax^2+\dfrac cax+\dfrac da=0
- 根据公式 m^3+3m^2n+3mn^2+n^3=(m+n)^3,配立方
x^3+3\left(\dfrac{b}{3a}\right)x^2=-\dfrac cax-\dfrac da
x^3+3\left(\dfrac{b}{3a}\right)x^2+3\left(\dfrac{b}{3a}\right)^2x+\left(\dfrac{b}{3a}\right)^3=-\dfrac cax-\dfrac da+3\left(\dfrac{b}{3a}\right)^2x+\left(\dfrac{b}{3a}\right)^3
\left(x+\dfrac{b}{3a}\right)^3=\dfrac{b^2-3ac}{3a^2}x+\dfrac{b^3-27a^2d}{27a^3}=\dfrac{b^2-3ac}{3a^2}\left(x+\dfrac{b}{3a}\right)+\dfrac{9abc-2b^3-27a^2d}{27a^3}
- 右边有 x 的一次项,无法直接开三次方根求解,考虑换元。令 X=x+\dfrac{b}{3a},则
X^3-\dfrac{b^2-3ac}{3a^2}X-\dfrac{9abc-2b^3-27a^2d}{27a^3}=0
X^3+\dfrac{3ac-b^2}{3a^2}X+\dfrac{2b^3+27a^2d-9abc}{27a^3}=0
- 令 p=\dfrac{3ac-b^2}{3a^2},q=\dfrac{2b^3+27a^2d-9abc}{27a^3},则只需解方程
X^3+pX+q=0
推导过程 - Part 2
先来看根的个数。
图:x^3-1.5x+1 图像,from GeoGebra
分类讨论
先研究 p<0 的情况。
- 对 f(x)=x^3+px+q 求导,得到 f'(x)=3x^2+p。
- 当 3x^2+p=0,即 \color{Blue}x=\pm\sqrt{-\dfrac p3} 时三次函数取取得极值。
- 将 x=-\sqrt{-\dfrac p3} 代入 f(x)=x^3+px+q 得 \color{Red}f(-\sqrt{-\dfrac p3})=-\dfrac{2p}{3}\sqrt{-\dfrac p3}+q。
- 当 x=0 时,f(x) 的纵截距为 f(0)=q,为\color{Yellow}黄色线段长度。
- 由于三次函数中心对称,所以可知\color{Green}绿色线段长度为 \color{Green}-\dfrac{2p}{3}\sqrt{-\dfrac{p}{3}}。
-
- 当 {\color{Yellow}黄}>{\color{Green}绿},即 \left(\dfrac p3\right)^3+\left(\dfrac q2\right)^2>0 时,三次方程有 1 个不等实根;
- 当 {\color{Yellow}黄}={\color{Green}绿},即 \left(\dfrac p3\right)^3+\left(\dfrac q2\right)^2=0 时,三次方程有 2 个不等实根;
- 当 {\color{Yellow}黄}<{\color{Green}绿},即 \left(\dfrac p3\right)^3+\left(\dfrac q2\right)^2<0 时,三次方程有 3 个不等实根。
再研究 p=0 的情况。
- 当 q\neq0 时,只有 1 个实根,此时符合 \left(\dfrac p3\right)^3+\left(\dfrac q2\right)^2>0;
- 当 q=0 时,同样只有 1 个不等实根,不符合 \left(\dfrac p3\right)^3+\left(\dfrac q2\right)^2=0 时的条件,所以要单独考虑。当然,也可以把这种情况定义为重根来去除例外。(要是考试出了这种题能坑死人)
最后研究 p>0 的情况。
当 p>0 时,有 1 个实根,此时 \left(\dfrac p3\right)^3+\left(\dfrac q2\right)^2>0,同样符合条件。
因为 \left(\dfrac p3\right)^3+\left(\dfrac q2\right)^2 在三次方程中的地位非常重要,且作用类似于二次方程的判别式,所以我们就把这个式子定义为三次方程判别式
\Delta=\left(\dfrac p3\right)^3+\left(\dfrac q2\right)^2
三次方程根的个数
$\Delta=0$ 时,有三个实根:
+ 当 $p=q=0$ 时,有一个三重零根;
+ 当 $\left(\dfrac p3\right)^3=-\left(\dfrac q2\right)^2\neq0$ 时,三个实根有两个相等;
$\Delta<0$ 时,有三个不等实根。
而**代数基本定理**告诉我们:任何复系数一元 $n$ 次多项式方程在复数域上有且只有 $n$ 个复根(不考虑重[chóng]根),所以一元三次方程必有三个复数根。
### 推导过程 - Part 3
上接 Part 1。
1. 将完全立方公式 $(u+v)^3=u^3+3u^2v+3uv^2+v^3$ 变形,得到 $(u+v)^3-3uv(u+v)-(u^3+v^3)=0$。
2. 将变形后的完全立方公式与 $X^3+pX+q=0$ 比对,可知对应系数相等的换元方法
$$\left\{\begin{matrix}X=u+v\quad(1)\\p=-3uv\quad(2)\\q=-u^3-v^3\quad(3)\end{matrix}\right.$$
3. 尝试解方程。将 $(2)$ 两边立方
$$u^3v^3=-\left(\dfrac p3\right)^3\quad(4)$$
4. 将 $(3)$ 两边同乘 $v^3$:
$$u^3v^3+(v^3)^2=-qv^3\quad(5)$$
5. 将 $(4)$ 代入 $(5)$ 并整理
$$(v^3)^2+qv^3-\left(\dfrac p3\right)^3=0\quad(6)$$
6. $(6)$ 是一个关于 $v^3$ 的二次方程。直接解方程得
$$v=\sqrt[3]{-\dfrac q2\pm\sqrt{\left(\dfrac p3\right)^3+\left(\dfrac q2\right)^2}}$$
7. 原方程关于 $u$,$v$ 对称,所以中间的 $\pm$ 共有三种情况:$u+$,$v-$;$u+$,$v+$;$u-$,$v-$。将这三种情况分别代入检验,发现只有
$$\left\{\begin{matrix}u=\sqrt[3]{-\dfrac q2+\sqrt{\left(\dfrac p3\right)^3+\left(\dfrac q2\right)^2}}\\v=\sqrt[3]{-\dfrac q2-\sqrt{\left(\dfrac p3\right)^3+\left(\dfrac q2\right)^2}}\end{matrix}\right.$$
8. 代入 $(1)$,得
$$X=\sqrt[3]{-\dfrac q2+\sqrt{\left(\dfrac p3\right)^3+\left(\dfrac q2\right)^2}}+\sqrt[3]{-\dfrac q2-\sqrt{\left(\dfrac p3\right)^3+\left(\dfrac q2\right)^2}}$$
9. 因为 $\left\{\begin{matrix}X=x+\dfrac{b}{3a}\\p=\dfrac{3ac-b^2}{3a^2}\\q=\dfrac{2b^3+27a^2d-9abc}{27a^3}\end{matrix}\right.$,所以三次方程的一个实根 $x_1$ 为
$$x_1=-\dfrac{b}{3a}+\sqrt[3]{-\dfrac{\dfrac{2b^3+27a^2d-9abc}{27a^3}}{2}+\sqrt{\left(\dfrac{\dfrac{3ac-b^2}{3a^2}}{3}\right)^3+\left(\dfrac{\dfrac{2b^3+27a^2d-9abc}{27a^3}}{2}\right)^2}}+\sqrt[3]{-\dfrac{\dfrac{2b^3+27a^2d-9abc}{27a^3}}{2}-\sqrt{\left(\dfrac{\dfrac{3ac-b^2}{3a^2}}{3}\right)^3+\left(\dfrac{\dfrac{2b^3+27a^2d-9abc}{27a^3}}{2}\right)^2}}$$
$$=-\dfrac{b}{3a}+\sqrt[3]{\dfrac{bc}{6a^2}-\dfrac{b^3}{27a^3}-\dfrac{d}{2a}+\sqrt{\left(\dfrac{bc}{6a^2}-\dfrac{b^3}{27a^3}-\dfrac{d}{2a}\right)^2+\left(\dfrac{c}{3a}-\dfrac{b^2}{9a^2}\right)^3}}+\sqrt[3]{\dfrac{bc}{6a^2}-\dfrac{b^3}{27a^3}-\dfrac{d}{2a}-\sqrt{\left(\dfrac{bc}{6a^2}-\dfrac{b^3}{27a^3}-\dfrac{d}{2a}\right)^2+\left(\dfrac{c}{3a}-\dfrac{b^2}{9a^2}\right)^3}}$$
但另外的两个根呢?
### 推导过程 - Part 4
1. 观察方程 $x^3=1$。判别式告诉我们只有一个实根。但在复数域中它应该有三个根。
2. 根据立方差公式,$x^3-1=(x-1)(x^2+x+1)=0$。左边括号里是实数根 $x_1=1$,右边括号里是另外的两个复数根。
3. 用二次方程求根公式解 $x^2+x+1=0$ 得 $x_{2,3}=\dfrac{-1\pm\sqrt3\text i}{2}$,$\dfrac{-1+\sqrt3\text i}{2}$ 就是三次单位虚根 $\omega$,满足性质 $\omega^2=\dfrac{-1-\sqrt3\text i}{2}$,$\omega^3=1$,且 $\omega$ 与 $\omega^2$ 共轭。
4. 请看 Part 3 的第 5 步到第 6 步的过程。满足 $x^3=1$ 的数除了 $1$ 还有 $\omega$ 和 $\omega^2$。
5. 所以我们就得到了三次方程的所有根:
$$x_1=-\dfrac{b}{3a}+u+v$$
$$x_2=-\dfrac{b}{3a}+\omega u+\omega^2v$$
$$x_3=-\dfrac{b}{3a}+\omega^2u+\omega v$$
与本章最开始形式相同。
> 注:$x_2$ 与 $x_3$ 共轭,可由求根公式直接推得。
### 推导过程 - 总结
总结一下推导方法。
1. 将一般三次方程 $ax^3+bx^2+cx+d=0$ $(a\neq0)$ 除以最高次项系数 $a$。
2. 设 $x=X-\dfrac{b}{3a}$,配立方后可将原方程化为 $X^3+pX+q=0$ 的形式。
3. 将 $X,p,q$ 用 $u,v$ 表达,并解出 $u,v$。
4. 将 $x$ 用 $u,v$ 还原,推导完毕。
### 求根公式的缺点
例如三次方程 $x^3-9x-28=0$,其实根为 $x=\sqrt[3]{14+\sqrt{14^2-3^2}}+\sqrt[3]{14-\sqrt{14^2-3^2}}=4$,计算很容易。
如果方程 $x^3-15x-4=0$,则由公式可得 $x=\sqrt[3]{2+11\sqrt{-1}}+\sqrt[3]{2-11\sqrt{-1}}$。
已知 $x=4$ 是方程 $x^3-15x-4=0$ 的根,因此 $\sqrt[3]{2+11\sqrt{-1}}+\sqrt[3]{2-11\sqrt{-1}}=4$ 成立。
那么如何把复数开三次方根呢?
## 根的三角函数表达式
对于经过简化后的三次方程 $x^3+px+q=0$ $(p<0,\Delta=\left(\dfrac p3\right)^3+\left(\dfrac q2\right)^2<0)$,三个实数根的三角函数表达式为:
$$x_1=2\sqrt[3]r\cos\theta$$
$$x_2=2\sqrt[3]r\cos\left(\theta+\dfrac{2\pi}{3}\right)$$
$$x_2=2\sqrt[3]r\cos\left(\theta+\dfrac{4\pi}{3}\right)$$
其中
$$r=\sqrt{-\left(\dfrac p3\right)^3},\theta=\dfrac13\arccos\left(-\dfrac{q}{2r}\right)$$
~~读者自证。~~
### 代码
```cpp
const complex<double> omega = {-0.5, sqrt(3) / 2}, omega2 = {-0.5, -sqrt(3) / 2};
vector<complex<double> > solve3_Cardano(double a, double b, double c, double d)
{
double p = (3 * a * c - b * b) / (3 * a * a), q = (27 * a * a * d - 9 * a * b * c + 2 * b * b * b) / (27 * a * a * a);
double delta = p * p * p / 27 + q * q / 4, k = -1 * b / (3 * a);
vector<complex<double> > x;
if(delta >= 0) // 有复数根
{
double t1 = -q / 2 + sqrt(delta), t2 = -q / 2 - sqrt(delta);
x.push_back(k + cbrt(t1) + cbrt(t2));
x.push_back(k + omega * cbrt(t1) + omega2 * cbrt(t2));
x.push_back(k + omega2 * cbrt(t1) + omega * cbrt(t2));
}
else // 无复数根
{
double r = sqrt(-pow((p / 3), 3)), theta = acos(-q / (2 * r)) / 3;
x.push_back(k + 2 * pow(r, 1. / 3) * cos(theta));
x.push_back(k + 2 * pow(r, 1. / 3) * cos(theta + Pi * 2 / 3));
x.push_back(k + 2 * pow(r, 1. / 3) * cos(theta + Pi * 4 / 3));
}
// 消除精度误差
for(auto &i : x)
{
if(abs(i.real()) < EPS)
i.real(0);
if(abs(i.imag()) < EPS)
i.imag(0);
}
return x;
}
```
代码中还有点问题:`else` 部分中为什么当 $\Delta<0$ 时 $p<0$ 呢?
原因很简单:$\Delta=\left(\dfrac p3\right)^3+\left(\dfrac q2\right)^2$,其中 $\left(\dfrac q2\right)^2\geq0$,所以 $\left(\dfrac p3\right)^3<0$,即 $p<0$。
这保证了代码不会 `RE`。
数学真神奇。
## 根与系数的关系
$$x_1+x_2+x_3=-\dfrac ba$$
$$\dfrac{1}{x_1}+\dfrac{1}{x_2}+\dfrac{1}{x_3}=-\dfrac cd$$
$$x_1x_2x_3=-\dfrac da$$
## [盛金公式](https://baike.baidu.com/item/盛金公式/10581722)
本质与卡尔达诺公式一样,不过计算量稍小。
盛金公式 4 基于三角函数,精度可能无法做到很高。
### 证明过程
|  |  |
| ------------------------------------------------------------ | ------------------------------------------------------------ |
|  |  |
### 代码
```cpp
vector<complex<double> > solve3_Shengjin(double a, double b, double c, double d)
{
double A = b * b - 3 * a * c, B = b * c - 9 * a * d, C = c * c - 3 * b * d;
double delta = B * B - 4 * A * C;
double x1, x2, x3, x2_im = 0, x3_im = 0;
if(delta < 0)
{
double T = (2 * A * b - 3 * a * B) / (2 * sqrt(A * A * A)), theta = acos(T);
x1 = (-b - 2 * sqrt(A) * cos(theta / 3)) / (3 * a);
x2 = (-b + sqrt(A) * (cos(theta / 3) + sqrt(3) * sin(theta / 3))) / (3 * a);
x3 = (-b + sqrt(A) * (cos(theta / 3) - sqrt(3) * sin(theta / 3))) / (3 * a);
}
if(delta > 0)
{
double y1 = A * b + 3 * a * (-B + sqrt(delta)) / 2, y2 = A * b + 3 * a * (-B - sqrt(delta)) / 2;
x1 = (-b - (cbrt(y1) + cbrt(y2))) / (3 * a);
x2 = x3 = (-b + (cbrt(y1) + cbrt(y2)) / 2) / (3 * a);
x2_im = sqrt(3) / 2 * (cbrt(y1) - cbrt(y2)) / (3 * a);
x3_im = -x2_im;
}
if(abs(delta) < EPS)
{
x1 = (-b / a) + B / A;
x2 = x3 = -B / A / 2;
}
if(abs(A) < EPS && abs(B) < EPS)
x1 = x2 = x3 = -b / (3 * a);
vector<complex<double> > x;
x.push_back(x1);
x.emplace_back(x2, x2_im);
x.emplace_back(x3, x3_im);
for(auto &i : x)
{
if(abs(i.real()) < EPS)
i.real(0);
if(abs(i.imag()) < EPS)
i.imag(0);
}
return x;
}
```
## 图像性质
任何一般的三次函数都能简化成 $x^3+px+q=0$,所以这里只研究 $x^3+px+q=0$ 的性质。
我们先来研究如何把三次函数简化。
### 三次函数的简化过程
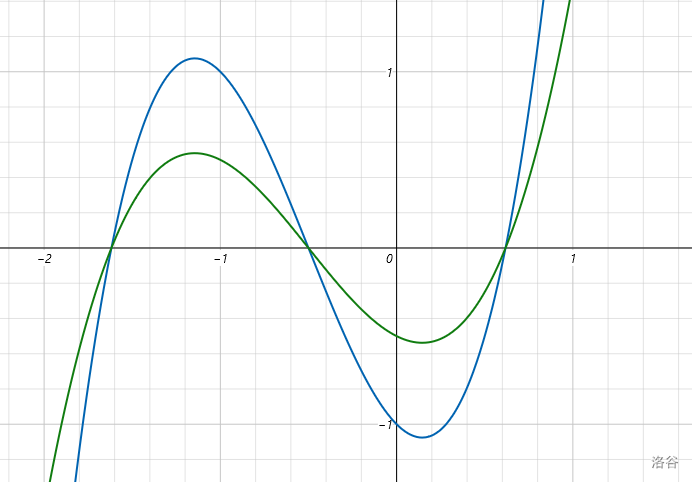
> 图 1:${\color{Blue}f(x)}=2x^3+3x^2-x-1$ 与 ${\color{Green}g(x)}=x^3+1.5x^2-0.5x-0.5$,from Windows Calculator
${\color{Blue}f(x)}=ax^3+bx^2+cx+d$ 先关于 $x$ 轴上下压缩 $a$ 倍(拉伸 $\dfrac1a$ 倍)变为 ${\color{Green}g(x)}=\dfrac{f(x)}{a}=x^3+\dfrac bax^2+\dfrac cax+\dfrac da$,零点不变。
---
我们尝试将拐点平移到 $y$ 轴上,来消去 $x^2$ 项。所有三次函数图像关于拐点都中心对称(即广义奇函数)。

> 图 2:${\color{Green}f(x)}=x^3+1.5x^2-0.5x-0.5$ 与 ${\color{Red}g(x)}=f(x-\dfrac{b}{3a})$,from Windows Calculator
对 $f(x)=x^3+\dfrac bax^2+\dfrac cax+\dfrac da$ 求两次导,得到 $f''(x)=6x+\dfrac{2b}{a}$。
令它等于 $0$ 然后求解,得到拐点横坐标 $x=-\dfrac{b}{3a}$,这与之前的三次函数求根公式的常数项 $-\dfrac{b}{3a}$ 相同。
$g(x)=f(x-\dfrac{b}{3a})=x^3+px+q$,就平移完成了,零点同样平移。
### 图像性质
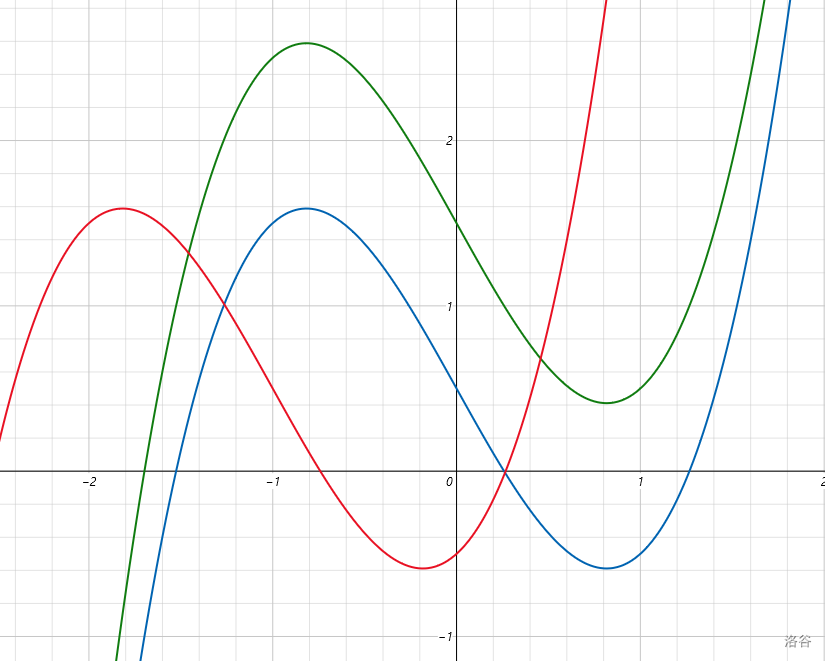
> 图 3:${\color{Blue}f(x)}=x^3-2x+0.5$,${\color{Green}g(x)}=f(x)+1=x^3-2x+0.5+1$,${\color{Red}h(x)}=f(x+1)=(x+1)^3-2(x+1)+0.5$ from Windows Calculator
> 上加下减,左加右减
$\color{Green}上加下减$:和二次函数类似,$q$ 代表纵截距,即函数与 $y$ 轴交点的 $y$ 坐标。
$q$ 增加 $n$,函数向上平移 $n$ 个单位;$q$ 减少 $n$,函数向下平移 $n$ 个单位。
$\color{Red}左加右减$:同样和二次函数类似,将每个 $x$ 替换成 $x+n$。
$n>0$时,函数向左平移 $n$ 个单位;$n<0$ 时,函数向右平移 $n$ 个单位。
## 总结
看了这些,你是不是觉得三次函数很简单?
> 确实很简单。
所以,我建议学校能够增加一些有关三次函数的内容,拓展大家的知识,也让我这篇文章能够有些用处。
# 4. 非精确(数值)求根
应用求根公式求出高次方程的根非常麻烦,而且五次及以上的方程没有通用的求根公式,但可以根据零点存在性定理求出方程的近似根。
## 零点存在性定理
若 $f(x)$ 在区间 $[a,b]$ 上是**连续不断的**,且 $f(a)f(b) < 0$,则 $f(x)$ 在区间 $(a,b)$ 上至少存在一个零点,即 $\exist x_0\in(a,b)$,$f(x_0)=0$。
## 二分法
由零点存在性定理,可以知道一种求函数零点近似解的方法:二分法。
二分法,顾名思义,就是每次把范围砍一半。
已知函数 $f(x)$ 在区间 $D$ 上存在根 $x^0$,求 $x^0$ 的近似值 $x$,并满足给定的精确度 `EPS`($\varepsilon$)。
```cpp
double f(double x)
{
return x * x * x - 5 * x * x - 4 * x + 20;
}
double solve(double l, double r)
{
while(r - l > EPS)
{
double mid = (l + r) / 2;
if(abs(f(mid)) < EPS)
return mid;
//if(f(l) > 0 && f(mid) > 0 || f(l) < 0 && f(mid) < 0)
if(f(l) * f(mid) > 0)
l = mid;
else
r = mid;
}
return (l + r) / 2;
}
```
由于区间每次取一半,所以复杂度是 $\log$ 级的。二分次数为 $\log(r-l)+\log\left(\dfrac1\varepsilon\right)$。
## 暴力方法
还有一种非常暴力的方法也放上来:
```cpp
void solve(double a, double b, double c, double d)
{
for(double i = -100; i <= 100; i += 0.001)
{
double j = i + 0.001;
double y1 = a*i*i*i + b*i*i + c*i + d;
double y2 = a*j*j*j + b*j*j + c*j + d;
//if(y1 >= 0 && y2 <= 0 || y1 <= 0 && y2 >= 0)
if(y1 * y2 <= 0)
printf("%.2lf ", (i + j) / 2);
}
}
```
## [牛顿迭代法](https://baike.baidu.com/item/牛顿迭代法/10887580)
牛顿迭代法(Newton's method)又称为牛顿-拉夫逊方法(Newton-Raphson method),它是牛顿在 17 世纪提出的一种在实数域和复数域上近似求解方程的方法,下文简称牛顿法。
设 $x$ 是 $f(x)$ 的根,取 $x_0$ 作为 $x$ 的初始近似值,则我们可以通过点 $(x_0,f(x_0))$ 作 $y=f(x)$ 的切线 $L_0:y=f(x_0)+f'(x_0)(x-x_0)$。
切线 $L$ 与 $x$ 轴有交点 $(x_1,0)$,$x_1=x_0-\dfrac{f(x_0)}{f'(x_0)}$ 为 $x$ 的 $1$ 次近似值。
我们再过点 $(x_1,f(x_1))$ 作 $y=f(x)$ 的切线 $L_1$,并求出 $L_1$ 与 $x$ 轴交点 $(x_2,0)$,$x_2=x_1-\dfrac{f(x_1)}{f'(x_1)}$ 为 $x$ 的 $2$ 次近似值。
这样迭代下去,$x$ 的 $n$ 次近似值 $\boxed{x_n=\dfrac{f(x_{n-1})}{f'(x_{n-1})}}$。
复杂度我不会算,但应该比二分法的复杂度低一些。
```cpp
double f(double x)
{
return x * x * x - 5 * x * x - 4 * x + 20;
}
double f_(double x) // f(x)的导函数f'(x)
{
return 3 * x * x - 10 * x - 4;
}
double solveNewton(double x)
{
while(abs(f(x)) > EPS)
x -= f(x) / f_(x);
return x;
}
```
这样,开平方的代码也能写出来了。
迭代函数:$f(x)=x^2-s$;
迭代公式:$x_{n+1}=x_n-\dfrac{f(x_n)}{f'(x_n)}=x_n-\dfrac{x_n^2-s}{2x_n}=\dfrac12\left(x_n+\dfrac{a}{x_n}\right)
double Sqrt(double s) // s >= 0
{
double x = s, y = (x + s / x) / 2;
while(abs(x - y) > EPS)
{
x = y;
y = (x + s / x) / 2;
}
return x;
}
精度
感谢评论区神犇 @Antarctic_Cube
可以证明,如果函数连续,并且待求的零点孤立,那么在零点周围存在一个区域,只要初始值位于这个邻近区域内,那么牛顿法必定收敛。
并且,如果不为 0,那么牛顿法将具有平方收敛的性能。即迭代一次后,误差将会在迭代前误差的平方乘上一个常数之内。
缺点
- 需要函数处处可导
- 近似根依赖于初始值的选取,每次只能求出一个根
- 切线导数不能为 0
- 方程无根就不能收敛(极少数情况有根也不能收敛,详细见下)
- 迭代结果可能出现循环节(详细见下)
刨去缺点不说,牛顿迭代法还是很好用的。
有根也不收敛的情况
例如 x^\frac13=0,此时唯一的根为 x=0。
对于牛顿法,需要求出 f(x)=x^\frac13=0 的导函数 f'(x)=\dfrac{1}{3x^\frac23},在 x=0 处不连续。而 x=0 恰好又是原函数的根,所以导致了在这种情况下有根也不收敛。
可能出现循环节的情况
例如 f(x)=x^4-x^2,x_0=\sqrt{\dfrac{3}{7}},迭代结果将在 \pm\sqrt{\dfrac{3}{7}} 内循环。
但是,大部分 OI 用的编程语言都不能无限精度表示浮点数(Python 很神奇,别跟我提 Python),所以每次浮点数计算都会有一定的精度误差,这点的精度误差导致了每次循环后结果都会稍有不同,多次循环(实测约 10 次)后精度就会偏差很大,导致仍然能算出正常结果。
平方根倒数速算法(0x5f3759df)
这是 Quake III 开源后人们从代码中找到的一段计算 \dfrac{1}{\sqrt n} 的代码:
float InvSqrt( float number )
{
long i;
float x2, y;
const float threehalfs = 1.5F;
x2 = number * 0.5F;
y = number;
i = * ( long * ) &y; // evil floating point bit level hacking
i = 0x5f3759df - ( i >> 1 ); // what the fuck?
y = * ( float * ) &i;
y = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration
// y = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration, this can be removed
return y;
}
速度比普通算法快 4 倍,一次迭代后精度约为 0.01,两次迭代后精度约为 0.00001。
程序首先猜测了一个接近 \dfrac{1}{\sqrt n} 的值,然后两次使用牛顿迭代法进行迭代。
运用牛顿迭代公式,可化简为$x'=x(1.5-0.5nx^2)$。迭代几次后,x的值将趋于$\dfrac{1}{\sqrt n}$。
至于那个 `0x5f3759df`,可以参考 [知乎上的解释](https://www.zhihu.com/question/26287650) 或者 [英文 wiki](https://en.wikipedia.org/wiki/Fast_inverse_square_root),里面涉及到了计算机底层数字表示方法(IEEE754),有点偏离文章主题,这里不多说了。
后来,又有人找(暴力枚举)出了比 `0x5f3759df` 更好的数:`0x5f375a86`,[论文链接](http://www.lomont.org/papers/2003/InvSqrt.pdf)。
论文中的推荐代码:
```cpp
float InvSqrt(float x)
{
float xhalf = 0.5f*x;
int i = *(int*)&x; // get bits for floating value
i = 0x5f375a86 - (i>>1); // gives initial guess y0
x = *(float*)&i; // convert bits back to float
x = x*(1.5f-xhalf*x*x); // Newton step, repeating increases accuracy
return x;
}
```
原理也一样。
当然现在在 OI 中大概没啥用了,不过还是要佩服当时人们想尽一切办法优化代码的精神。
## 割线法
为了解决牛顿迭代法中函数需要求导的缺点,可以将函数的割线代替切线,从而得到割线法。
### 割线
给定函数 $f(x)$ 上两点 $(x_{n-1},f(x_{n-1}))$ 和 $(x_n,f(x_n))$,经过这两点的直线即为割线,方程为
$$y-f(x_n)=k(x-x_n)$$
其中割线斜率 $k$ 为
$$k=\dfrac{f(x_n)-f(x_{n-1})}{x_n-x_{n-1}}$$
### 割线法
给定 $x_{n-1}$ 和 $x_n$,设 $x_{n+1}$ 为过两点的割线与 $x$ 轴交点的横坐标,有
$$-f(x_n)=k(x_{n+1}-x_n)$$
解得
$$x_{n+1}=x_n-\dfrac{f(x_n)}{k}=x_n-\dfrac{x_n-x_{n-1}}{f(x_n)-f(x_{n-1})}f(x_n)$$
多次迭代后结果越来越精确。
说白了就是将牛顿法中切线斜率 $f'(x_n)$ 用割线斜率 $\dfrac{f(x_n)-f(x_{n-1})}{x_n-x_{n-1}}$ 代替。
复杂度比牛顿法略高,但适用范围更广。
### 代码
```cpp
double f(double x)
{
return x * x * x - 5 * x * x - 4 * x + 20;
}
double solveSecant(double x0, double x1)
{
double x;
while(abs(x1 - x0) > EPS)
{
x = x1 - f(x1) * (x1 - x0) / (f(x1) - f(x0));
x0 = x1;
x1 = x;
}
return x;
}
```
## 效率比较
测试执行的 `while` 循环次数。
测试中浮点数均使用 `long double` 类型,`EPS = 1e-12`。
注:测试数据仅能代表相对效率,不考虑每次循环中运算次数。
| 测试方程 | 二分法 | 牛顿法 | 割线法 |
|:----------------------:|:------:|:------:|:------:|
| $13x^3+21x^2+14x+28=0$ | ~45 | 6~15 | 8~18 |
| $\sqrt[3]{x}+2=0$ | ~45 | nan | 8~10 |
# 5. 四次方程
形如 $ax^4+bx^3+cx^2+dx+e=0$ $(a\neq0)$ 的方程叫做一元四次方程。
## 求根公式
对于一元四次方程
$$ax^4+bx^3+cx^2+dx+e=0$$
记
$$\Delta_1=c^2-3bd+12ae$$
$$\Delta_2=2c^3-9bcd+27ad^2+27b^2e-72ace$$
并记
$$\Delta=\dfrac{\sqrt[3]{2}\Delta_{1}}{3a\sqrt[3]{\Delta_{2}+\sqrt{-4\Delta_{1}^{3}+\Delta_{2}^{2}}}}+\dfrac{\sqrt[3]{\Delta_{2}+\sqrt{-4\Delta_{1}^{3}+\Delta_{2}^{2}}}}{3\sqrt[3]{2}a}$$
则有
$$x_{1}=-\dfrac{b}{4a}-\dfrac12\sqrt{\dfrac{b^{2}}{4a^{2}}-\dfrac{2c}{3a}+\Delta}-\dfrac12\sqrt{\dfrac{b^{2}}{2a^{2}}-\dfrac{4c}{3a}-\Delta-\dfrac{-\dfrac{b^{3}}{a^{3}}+\dfrac{4bc}{a^{2}}-\dfrac{8d}{a}}{4\sqrt{\dfrac{b^{2}}{4a^{2}}-\dfrac{2c}{3a}+\Delta}}}$$
$$x_{2}=-\dfrac{b}{4a}-\dfrac12\sqrt{\dfrac{b^{2}}{4a^{2}}-\dfrac{2c}{3a}+\Delta}+\dfrac12\sqrt{\dfrac{b^{2}}{2a^{2}}-\dfrac{4c}{3a}-\Delta-\dfrac{-\dfrac{b^{3}}{a^{3}}+\dfrac{4bc}{a^{2}}-\dfrac{8d}{a}}{4\sqrt{\dfrac{b^{2}}{4a^{2}}-\dfrac{2c}{3a}+\Delta}}}$$
$$x_{3}=-\dfrac{b}{4a}+\dfrac12\sqrt{\dfrac{b^{2}}{4a^{2}}-\dfrac{2c}{3a}+\Delta}-\dfrac12\sqrt{\dfrac{b^{2}}{2a^{2}}-\dfrac{4c}{3a}-\Delta+\dfrac{-\dfrac{b^{3}}{a^{3}}+\dfrac{4bc}{a^{2}}-\dfrac{8d}{a}}{4\sqrt{\dfrac{b^{2}}{4a^{2}}-\dfrac{2c}{3a}+\Delta}}}$$
$$x_{4}=-\dfrac{b}{4a}+\dfrac12\sqrt{\dfrac{b^{2}}{4a^{2}}-\dfrac{2c}{3a}+\Delta}+\dfrac12\sqrt{\dfrac{b^{2}}{2a^{2}}-\dfrac{4c}{3a}-\Delta+\dfrac{-\dfrac{b^{3}}{a^{3}}+\dfrac{4bc}{a^{2}}-\dfrac{8d}{a}}{4\sqrt{\dfrac{b^{2}}{4a^{2}}-\dfrac{2c}{3a}+\Delta}}}$$
完整版的太长了,放文章最后。
### 推导方法
> 人类的智慧是无穷的。
1. 按照惯例,先除掉最高次项:
$$x^4+\dfrac bax^3+\dfrac cax^2+\dfrac dax+\dfrac ea=0$$
2. 确定平移量:
+ 二次方程平移量(求 $1$ 次导):$-\dfrac{b}{2a}
- 三次方程平移量(求 2 次导):-\dfrac{b}{3a}
- 四次方程平移量(求 3 次导):-\dfrac{b}{4a}
- 将 x=x-\dfrac{b}{4a} 代入上式并展开,就能够消去三次项:
x^4+px^2+qx+r=0
p=\dfrac{c}{a}-\dfrac{3 b^2}{8 a^2}
q=\dfrac{b^3}{8 a^3}-\dfrac{b c}{2 a^2}+\dfrac{d}{a}
r=-\dfrac{3 b^4}{256 a^4}+\dfrac{b^2 c}{16 a^3}-\dfrac{b d}{4 a^2}+\dfrac{e}{a}
- 根据这个,我们可以知道四次方程的求根公式前面有一个 -\dfrac{b}{4a}。
- 移项,凑完全平方:
x^4+px^2+px^2+p^2=-qx-r+px^2+p^2
(x^2+p)^2=px^2-qx+p^2-r
- 为了让右边也是完全平方,我们引入新变量 z,同时左边也要保证是完全平方:
(x^2+p)^2{\color{Red}+2(x^2+p)z+z^2}=px^2-qx+p^2-r{\color{Red}+2(x^2+p)z+z^2}
(x^2+p+z)^2=(p+2z)x^2-qx+(p^2+2pz+z^2-r)
- 尝试选取适当的 z,使得右面也是完全平方式,这样我们就可以变形为:
x^2+p+z=\pm(Sx+T)
- 为了让右面是完全平方式,所以让 \Delta=0,得:
q^2-4(p+2z)(p^2+2pz+z^2-r)=0
-8z^3-20pz^2(-16p^2+8r)z-4p^3+q^2+4pr=0
8z^3+20pz^2+(16p^2-8r)z+4p^3-q^2-4pr=0
- 这是一个关于 z 的三次方程,我们已经知道怎么求解了。
- 解出 z 后,将 z 代入,解第 6 步的方程,就得到了四次方程的四个根。
另一种推导方法
-
按照惯例,先除掉最高次项:
x^4+\dfrac bax^3+\dfrac cax^2+\dfrac dax+\dfrac ea=0
-
确定平移量:
- 二次方程平移量(求 1 次导):-\dfrac{b}{2a}
- 三次方程平移量(求 2 次导):-\dfrac{b}{3a}
- 四次方程平移量(求 3 次导):-\dfrac{b}{4a}
-
将 x=x-\dfrac{b}{4a} 代入上式并展开,就能够消去三次项:
x^4+px^2+qx+r=0
p=\dfrac{c}{a}-\dfrac{3 b^2}{8 a^2}
q=\dfrac{b^3}{8 a^3}-\dfrac{b c}{2 a^2}+\dfrac{d}{a}
r=-\dfrac{3 b^4}{256 a^4}+\dfrac{b^2 c}{16 a^3}-\dfrac{b d}{4 a^2}+\dfrac{e}{a}
-
由代数基本定理,可知一元四次方程有四个根,记为 x_1,x_2,x_3,x_4。其中任意两个根可看作是一个二次方程的根,剩下的两个根又是另外一个二次方程的根。因此,任意最高次项系数为 1 的四次方程都可化为以下形式:
(x^2+\alpha x+\beta)(x^2+\lambda x+\mu)=0
-
设二次多项式 A 和一次多项式 B 满足
A+B=x^2+\alpha x+\beta\\
A-B=x^2+\lambda x+\mu
\end{matrix}\right.
即
(x^2+\alpha x+\beta)(x^2+\lambda x+\mu)=(A+B)(A-B)=A^2-B^2=0
-
对三次项为 0 的四次方程 x^4+px^2+qx+r=0,设 A=x^2+\omega 且 B=\sqrt k(x+\varphi)(起名字困难症),其中 A 无一次项,不然所得的四次方程就有三次项了(读者自证)。
-
展开,得到
x^4+0x^3+px^2+qx+r=x^4+0x^3+(2\omega-k)x^2-2k\varphi x+(\omega^2-k\varphi^2)=0
-
依照国际惯例,比较对应系数相等,得到关于 k,\omega,\varphi 的三元方程组
2\omega-k=p\\
-2k\varphi=q\\
\omega^2-k\varphi^2=r
\end{matrix}\right.
-
转化方程可得一个关于 k 的三次方程
k^3+2pk^2+(p^2-4r)k-q^2=0
-
三次方程我们会解。解出 k 后,我们就可以得到 \omega,\varphi 与 A 和 B 了。
-
得到 A,B 后,还原出两个四次方程的因式,就可知四次方程求根公式了。这里直接给出。
对于约掉三次项后的四次方程 x^4+px^2+qx+r=0,其求根公式为:
x_1=\dfrac{-\sqrt k+\sqrt{k-4\omega-4\varphi\sqrt k}}{2}
x_2=\dfrac{-\sqrt k-\sqrt{k-4\omega-4\varphi\sqrt k}}{2}
x_3=\dfrac{\sqrt k+\sqrt{k-4\omega+4\varphi\sqrt k}}{2}
x_4=\dfrac{\sqrt k-\sqrt{k-4\omega+4\varphi\sqrt k}}{2}
其中
k=-\dfrac{2p}{3}+\sqrt[3]{-\dfrac Q2+\sqrt{\left(\dfrac P3\right)^3+\left(\dfrac Q2\right)^2}}+\sqrt[3]{-\dfrac Q2-\sqrt{\left(\dfrac P3\right)^3+\left(\dfrac Q2\right)^2}}
\omega=\dfrac{p+k}{2}
\varphi=\dfrac{q}{2k}
P=\dfrac{-p^2-12r}{3}
Q=\dfrac{72pr-2p^3-27q^2}{27}
代码
懒得写。
可参考 洛谷日报。
待定系数法
如果有理系数四次方程有有理根,则可通过上文提到过的试根法来因式分解;
如果有理系数四次方程无有理根,则只能通过待定系数法来解。
例:在实数范围内解方程 x^4+2x^3−x^2+2x+1=0。
解:
- 方程的有理根只可能为 \pm1,\pm3,但都不能是方程左边为 0,所以方程无有理根,因此也没有(有理系数的)一次因式。
- 既然无法分解成有理系数的一次因式,那么只能分解成两个有理系数的二次因式。考虑待定系数法。
- 因为最高次项系数为 1,设 x^4+2x^3−x^2+2x+1=(x^2+ax+b)(x^2+cx+d),a,b,c,d\in\mathbb Z
- 展开等式右边,比较相同次项的系数,得 \left\{\begin{matrix}a+c=2\\b+d+ac=-1\\bc+ad=2\\bd=1\end{matrix}\right.
- 解方程组得 \left\{\begin{matrix}a=-1\\b=1\\c=3\\d=1\end{matrix}\right.
- 则原方程能够因式分解成 (x^2-x+1)(x^2+3x+1)=0。
-
- 原方程的实数解为 x_{1,2}=\dfrac{-3\pm\sqrt5}{2}。
6. 高次方程
形如 a_nx^n+a_{n-1}x^n-1+\dots+a_1x+a_n=0 的方程叫做一元 n 次方程。
根据伽罗瓦理论,五次及以上方程无公式通解。
高次方程求根公式
$1$ 到 $4$ 次方程的通用求根公式的推导都需要人类智慧。那有没有不需要人类智慧的方法呢?
群论。
伽罗瓦提出了一个理论:
代数方程能用根式解的充分必要条件是其伽罗瓦群为可解群,即一元 $n$ 次方程能用根式解的充要条件是 $n$ 阶伽罗瓦群可解,反之也成立。
因为 $5$ 阶及以上伽罗瓦群不可解,所以 $5$ 次及以上的方程无通用根式解。
> 注:不代表 $5$ 次及以上的方程就没有解:
> 比如 $x^5−2x^4−18x^3+4x^2+49x+30=0
采用试根法能很容易的因式分解成 (x−5)(x−2)(x+1)^2(x+3)=0
因此五个根分别为 x_1=5,x_2=2,x_{3,4}=-1,x_5=-3
详细内容可参考妈咪说的视频 #1 #2 #3 #4 #5 #6,里面详细介绍了群论的基础以及这一部分的证明方法,强烈推荐。
也可参考前面的洛谷日报 #382 和 #384。
Dummit 判别法
Dummit 在 1991 年的一篇论文中提出了一种方法,可以判断任意一个系数均为有理数的五次方程是否有根式解。
依照惯例,先除掉五次项的系数,再消去四次项。
ax^5+bx^4+cx^3+dx^2+ex+f=0(a\neq0)
x^5+\dfrac bax^4+\dfrac cax^3+\dfrac dax^2+\dfrac eax+\dfrac fa=0
将 x=X-\dfrac{b}{5a} 代入,展开可得
X^5+\left(\dfrac{c}{a}-\dfrac{2b^2}{5a^2}\right)X^3+\left(\dfrac{4b^3}{25a^3}-\dfrac{3bc}{5a^2}+\dfrac{d}{a}\right)X^2+\left(-\dfrac{3b^4}{125a^4}+\dfrac{3b^2c}{25a^3}-\dfrac{2bd}{5a^2}+\dfrac{e}{a}\right)X+\dfrac{4b^5}{3125a^5}-\dfrac{b^3c}{125a^4}+\dfrac{b^2d}{25a^3}-\dfrac{be}{5a^2}+\dfrac{f}{a}
令
p=\dfrac{c}{a}-\dfrac{2b^2}{5a^2}
q=\dfrac{4b^3}{25a^3}-\dfrac{3bc}{5a^2}+\dfrac{d}{a}
r=-\dfrac{3b^4}{125a^4}+\dfrac{3b^2c}{25a^3}-\dfrac{2bd}{5a^2}+\dfrac{e}{a}
s=\dfrac{4b^5}{3125a^5}-\dfrac{b^3c}{125a^4}+\dfrac{b^2d}{25a^3}-\dfrac{be}{5a^2}+\dfrac{f}{a}
则有
X^5+pX^3+qX^2+rX+s=0
\dots
link
(太纯粹了,OI 中无实际应用价值,不写了)
附:四次方程求根公式
博客放不下,所以:
云剪贴板链接
[\underline{\overline{\ddot\smile}}]\quad(\undergroup{\overgroup{\ddot\smile}})
〈__,.ヘヽ. / ,ー、 〉
\ ', !-─‐-i / /´
/`ー' L//`ヽ、
/ /, /| , , ',
イ / /-‐/ i L_ ハ ヽ! i
レ ヘ 7イ`ト レ'ァ-ト、!ハ| |
!,/7 '0' ´0iソ| |
|.从" _ ,,,, / |./ |
レ'| i>.、,,__ _,.イ / .i |
レ'| | / k_7_/レ'ヽ, ハ. |
| |/i 〈|/ i ,.ヘ | i |
.|/ / i: ヘ! \ |
kヽ>、ハ _,.ヘ、 /、!
!'〈//`T´', \ `'7'ーr'
レ'ヽL__|___i,___,ンレ|ノ
ト-,/ |___./
'ー' !_,.: